Дифференцируемая кривая
Дифференциальная геометрия кривых — раздел геометрии , изучающий гладкие кривые на плоскости и в евклидовом пространстве методами дифференциального и интегрального исчисления .
Многие конкретные кривые были тщательно исследованы с использованием синтетического подхода . Дифференциальная геометрия идет другим путем: кривые представлены в параметризованной форме , а их геометрические свойства и различные величины, связанные с ними, такие как кривизна и длина дуги , выражаются через производные и интегралы с использованием векторного исчисления . Одним из наиболее важных инструментов, используемых для анализа кривой, является рамка Френе , подвижная рамка, которая обеспечивает систему координат в каждой точке кривой, которая «наилучшим образом адаптирована» к кривой вблизи этой точки.
Теория кривых намного проще и уже по охвату, чем теория поверхностей и ее обобщения более высоких размерностей, поскольку регулярная кривая в евклидовом пространстве не имеет внутренней геометрии. Любая регулярная кривая может быть параметризована длиной дуги ( естественная параметризация ). С точки зрения теоретической точечной частицы на кривой, которая ничего не знает об окружающем пространстве, все кривые будут выглядеть одинаково. Различные пространственные кривые отличаются только тем, как они изгибаются и скручиваются. Количественно это измеряется дифференциально-геометрическими инвариантами, называемыми кривизной и кручением кривой . Основная теорема о кривых утверждает, что знание этих инвариантов полностью определяет кривую.
Определения
Параметрическая C r - кривая или C r - параметризация - это векторная функция , которая непрерывно дифференцируема r раз (то есть, компоненты функций γ непрерывно дифференцируемы), где , , и I - непустой интервал действительных чисел. Образ параметрической кривой - это . Параметрическую кривую γ и ее образ γ [ I ] следует различать, поскольку заданное подмножество может быть образом многих различных параметрических кривых. Параметр t в γ ( t ) можно рассматривать как представление времени, а γ - траекторию движущейся точки в пространстве. Когда I - замкнутый интервал [ a , b ] , γ ( a ) называется начальной точкой, а γ ( b ) - конечной точкой γ . Если начальная и конечная точки совпадают (то есть γ ( a ) = γ ( b ) ), то γ является замкнутой кривой или петлей . Чтобы быть C r -циклом, функция γ должна быть r -кратно непрерывно дифференцируемой и удовлетворять γ ( k ) ( a ) = γ ( k ) ( b ) для 0 ≤ k ≤ r .
Параметрическая кривая проста , если инъективна . Она аналитична , если каждая компонентная функция γ является аналитической функцией , то есть принадлежит классу C ω .
Кривая γ является регулярной порядка m (где m ≤ r ), если для любого t ∈ I является линейно независимым подмножеством . В частности, параметрическая C 1 -кривая γ является регулярной тогда и только тогда, когда γ ′ ( t ) ≠ 0 для любого t ∈ I .
Репараметризация и отношение эквивалентности
Учитывая изображение параметрической кривой, существует несколько различных параметризаций параметрической кривой. Дифференциальная геометрия стремится описать свойства параметрических кривых, которые инвариантны относительно определенных репараметризаций. Должно быть определено подходящее отношение эквивалентности на множестве всех параметрических кривых. Дифференциально-геометрические свойства параметрической кривой (такие как ее длина, ее рамка Френе и ее обобщенная кривизна) инвариантны относительно репараметризации и, следовательно, являются свойствами самого класса эквивалентности . Классы эквивалентности называются C r -кривыми и являются центральными объектами, изучаемыми в дифференциальной геометрии кривых.
Две параметрические кривые C r и называются эквивалентными тогда и только тогда , когда существует биективное Cr -отображение φ : I 1 → I 2 такое, что и γ 2 тогда называется повторной параметризацией γ 1 .
Репараметризация определяет отношение эквивалентности на множестве всех параметрических C r -кривых класса C r . Класс эквивалентности этого отношения — просто C r -кривая.
Еще более тонкое отношение эквивалентности ориентированных параметрических кривых C r можно определить, потребовав, чтобы φ удовлетворяло условию φ ′ ( t ) > 0 .
Эквивалентные параметрические C r -кривые имеют одинаковое изображение, а эквивалентные ориентированные параметрические C r -кривые даже пересекают изображение в одном и том же направлении.
Длина и естественная параметризация
Длина l параметрической C 1 -кривой определяется как Длина параметрической кривой инвариантна относительно репараметризации и, следовательно, является дифференциально-геометрическим свойством параметрической кривой.
Для каждой регулярной параметрической кривой C r , где r ≥ 1 , функция определяется записью γ (s) = γ ( t ( s ) ) , где t ( s ) — обратная функция s ( t ) . Это перепараметризация γ функции γ , которая называетсяпараметризация длины дуги , натуральная параметризация,параметризацияединичной скорости. Параметр s ( t )называетсянатуральным параметромγ.
Эта параметризация предпочтительна, поскольку естественный параметр s ( t ) пересекает изображение γ с единичной скоростью, так что На практике часто очень сложно вычислить естественную параметризацию параметрической кривой, но она полезна для теоретических рассуждений.
Для заданной параметрической кривой γ естественная параметризация единственна с точностью до сдвига параметра.
Эту величину иногда называют энергией или действием кривой; это название оправдано, поскольку уравнения геодезической являются уравнениями движения Эйлера–Лагранжа для этого действия.
Рамка Френе
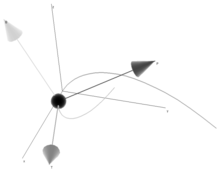
Система Френе — это подвижная система отсчета из n ортонормированных векторов e i ( t ) , которые используются для описания кривой локально в каждой точке γ ( t ) . Это основной инструмент в дифференциально-геометрической обработке кривых, поскольку гораздо проще и естественнее описывать локальные свойства (например, кривизну, кручение) в терминах локальной системы отсчета, чем использовать глобальную, такую как евклидовы координаты.
Для C n + 1 -кривой γ, в которой является регулярной порядка n, рамка Френе для кривой представляет собой набор ортонормальных векторов, называемых векторами Френе . Они строятся из производных γ ( t ) с использованием алгоритма ортогонализации Грама-Шмидта с
Действительные функции χ i ( t ) называются обобщенными кривизнами и определяются как
Рамка Френе и обобщенные кривизны инвариантны относительно репараметризации и, следовательно, являются дифференциально-геометрическими свойствами кривой. Для кривых в — кривизна, а — кручение.
кривая Бертрана
Кривая Бертрана — это регулярная кривая в с дополнительным свойством, заключающимся в том, что существует вторая кривая в , такая, что главные нормальные векторы к этим двум кривым идентичны в каждой соответствующей точке. Другими словами, если γ 1 ( t ) и γ 2 ( t ) — две кривые в , такие, что для любого t две главные нормали N 1 ( t ), N 2 (t) равны, то γ 1 и γ 2 — кривые Бертрана, а γ 2 называется сопряжением Бертрана для γ 1 . Мы можем записать γ 2 ( t ) = γ 1 ( t ) + r N 1 ( t ) для некоторой константы r . [1]
Согласно задаче 25 в работе Кюнеля «Дифференциальная геометрия кривых – поверхностей – многообразий», также верно, что две кривые Бертрана, которые не лежат в одной и той же двумерной плоскости, характеризуются существованием линейной связи a κ ( t ) + b τ ( t ) = 1 , где κ ( t ) и τ ( t ) являются кривизной и кручением γ 1 ( t ) , а a и b являются действительными константами с a ≠ 0 . [2] Более того, произведение кручений пары кривых Бертрана является константой. [3] Если γ 1 имеет более одного сопряжения Бертрана, то их бесконечно много. Это происходит только тогда, когда γ 1 является круговой спиралью. [1]
Специальные векторы Френе и обобщенные кривизны
Первые три вектора Френе и обобщенные кривизны можно визуализировать в трехмерном пространстве. Они имеют дополнительные имена и больше семантической информации, прикрепленной к ним.
Касательный вектор
Если кривая γ представляет собой траекторию частицы, то мгновенная скорость частицы в данной точке P выражается вектором , называемым касательным вектором к кривой в точке P. Математически, если задана параметризованная кривая C 1 γ = γ ( t ) , для каждого значения t = t 0 параметра вектор является касательным вектором в точке P = γ ( t 0 ) . Вообще говоря, касательный вектор может быть равен нулю . Величина касательного вектора является скоростью в момент времени t 0 .
Первый вектор Френе e 1 ( t ) — это единичный касательный вектор в том же направлении, определенный в каждой регулярной точке γ : Если t = s — натуральный параметр, то касательный вектор имеет единичную длину. Формула упрощается: Единичный касательный вектор определяет ориентацию кривой или прямое направление, соответствующее возрастающим значениям параметра. Единичный касательный вектор, взятый в качестве кривой, отслеживает сферическое изображение исходной кривой.
Вектор нормали или вектор кривизны
Вектор нормали кривой , иногда называемый вектором кривизны , указывает на отклонение кривой от прямой линии. Он определяется как
Его нормализованная форма, единичный нормальный вектор, является вторым вектором Френе e 2 ( t ) и определяется как
Касательная и нормальный вектор в точке t определяют соприкасающуюся плоскость в точке t .
Можно показать, что ē 2 ( t ) ∝ e ′ 1 ( t ) . Следовательно,
Кривизна
Первая обобщенная кривизна χ 1 ( t ) называется кривизной и измеряет отклонение γ от прямой линии относительно соприкасающейся плоскости. Она определяется как и называется кривизной γ в точке t . Можно показать , что
Величина , обратная кривизне, называется радиусом кривизны .
Окружность радиусом r имеет постоянную кривизну, тогда как линия имеет кривизну, равную 0.
Бинормальный вектор
Единичный бинормальный вектор — это третий вектор Френе e 3 ( t ) . Он всегда ортогонален единичным касательным и нормальным векторам в точке t . Он определяется как
В трехмерном пространстве уравнение упрощается до или до То, что может встречаться любой из знаков, иллюстрируется примерами правозакрученной и левозакрученной спирали.
Торсион
Вторая обобщенная кривизна χ 2 ( t ) называется кручением и измеряет отклонение γ от того, чтобы быть плоской кривой . Другими словами, если кручение равно нулю, кривая полностью лежит в той же соприкасающейся плоскости (существует только одна соприкасающаяся плоскость для каждой точки t ). Она определяется как и называется кручением γ в точке t .
Аберрантность
Третья производная может быть использована для определения аберрантности , метрики некруглости кривой. [4] [5] [6]
Основная теорема теории кривых
Дано n − 1 функций: тогда существует единственная (с точностью до преобразований с использованием евклидовой группы ) C n + 1 -кривая γ , которая является регулярной порядка n и обладает следующими свойствами: где множество является фреймом Френе для кривой.
Дополнительно предоставляя начальную точку t 0 в I , начальную точку p 0 в и начальную положительную ортонормированную систему координат Френе { e 1 , ..., e n − 1 } с евклидовыми преобразованиями, можно исключить, получив единственную кривую γ .
Формулы Френе-Серре
Формулы Френе–Серре представляют собой набор обыкновенных дифференциальных уравнений первого порядка. Решением является набор векторов Френе, описывающих кривую, заданную обобщенными функциями кривизны χ i .
2 измерения
3 измерения
нразмеры (общая формула)
Смотрите также
Ссылки
- ^ ab do Carmo, Manfredo P. (2016). Дифференциальная геометрия кривых и поверхностей (пересмотренное и обновленное 2-е изд.). Минеола, Нью-Йорк: Dover Publications, Inc. стр. 27–28. ISBN 978-0-486-80699-0.
- ^ Кюнель, Вольфганг (2005). Дифференциальная геометрия: кривые, поверхности, многообразия . Провиденс: AMS. стр. 53. ISBN 0-8218-3988-8.
- ^ Вайсштейн, Эрик В. «Кривые Бертрана». mathworld.wolfram.com .
- ^ Шот, Стивен (ноябрь 1978 г.). «Аберрантность: геометрия третьей производной». Mathematics Magazine . 5. 51 (5): 259–275. doi :10.2307/2690245. JSTOR 2690245.
- ^ Кэмерон Байерли; Рассел А. Гордон (2007). «Меры аберрантности». Real Analysis Exchange . 32 (1). Michigan State University Press: 233. doi : 10.14321/realanalexch.32.1.0233 . ISSN 0147-1937.
- ^ Гордон, Рассел А. (2004). «Аберрантность плоских кривых». The Mathematical Gazette . 89 (516). Cambridge University Press (CUP): 424–436. doi :10.1017/s0025557200178271. ISSN 0025-5572. S2CID 118533002.
Дальнейшее чтение
- Крейциг, Эрвин (1991). Дифференциальная геометрия . Нью-Йорк: Dover Publications. ISBN 0-486-66721-9.Глава II представляет собой классическое изложение теории кривых в трехмерном пространстве.



![{\displaystyle \gamma [I]\subseteq \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27a675bd019e880d10ce7c4e1f744884fa8afab8)







![{\displaystyle \gamma :[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac70dec799b73a718bdc3431587a65f829bf03b)

![{\displaystyle \forall t\in [a,b]:\quad s(t)~{\stackrel {\text{def}}{=}}~\int _{a}^{t}\left\|\gamma '(x)\right\|\,\mathrm {d} {x}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/213ccdcd8b5a360dfd7b10af5ec2acb0d2af44eb)



![{\displaystyle {\begin{aligned}\mathbf {e} _{1}(t)&={\frac {{\boldsymbol {\gamma }}'(t)}{\left\|{\boldsymbol {\gamma }}'(t)\right\|}}\\[1ex]\mathbf {e} _{j}(t)&={\frac {{\overline {\mathbf {e} _{j}}}(t)}{\left\|{\overline {\mathbf {e} _{j}}}(t)\right\|}},&{\overline {\mathbf {e} _{j}}}(t)&={\boldsymbol {\gamma }}^{(j)}(t)-\sum _{i=1}^{j-1}\left\langle {\boldsymbol {\gamma }}^{(j)}(t),\,\mathbf {e} _{i}(t)\right\rangle \,\mathbf {e} _{i}(t){\vphantom {\Bigg \langle }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7a438a21715348108d363a47e7decbe61ca55c9)



















![{\displaystyle \chi _{i}\in C^{ni}([a,b],\mathbb {R} ^{n}),\quad \chi _{i}(t)>0,\quad 1\leq i\leq n-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7182200998b9129906844a4064319c58db58284)
![{\displaystyle {\begin{align}\|\gamma '(t)\|&=1&t\in [a,b]\\\chi _{i}(t)&={\frac {\langle \mathbf {e} _{i}'(t),\mathbf {e} _{i+1}(t)\rangle }{\|{\boldsymbol {\gamma }}'(t)\|}}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dea14cc28063056837a1e8fcc22afbdcc9de4b49)


![{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\[0.75ex]\mathbf {e} _{2}'(t)\\[0.75ex]\mathbf { e} _{3}'(t)\end{bmatrix}}=\left\Vert \gamma '(t)\right\Vert {\begin{bmatrix}0&\kappa (t)&0\\[1ex]- \kappa (t)&0&\tau (t)\\[1ex]0&-\tau (t)&0\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\ [1ex]\mathbf {e} _{2}(t)\\[1ex]\mathbf {e} _{3}(t)\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b2b3f14415be28c04fe7791330e1a80312da4c0)
![{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\[1ex]\mathbf {e} _{2}'(t)\\[1ex]\vdots \\[ 1ex]\mathbf {e} _{n-1}'(t)\\[1ex]\mathbf {e} _{n}'(t)\\[1ex]\end{bmatrix}}=\left\ Vert \gamma '(t)\right\Vert {\begin{bmatrix}0&\chi _{1}(t)&\cdots &0&0\\[1ex]-\chi _{1}(t)&0&\cdots &0&0 \\[1ex]\vdots &\vdots &\ddots &\vdots &\vdots \\[1ex]0&0&\cdots &0&\chi _{n-1}(t)\\[1ex]0&0&\cdots &-\chi _{n-1}(t)&0\\[1ex]\end{ bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\[1ex]\mathbf {e} _{2}(t)\\[1ex]\vdots \\[1ex] \mathbf {e} _{n-1}(t)\\[1ex]\mathbf {e} _{n}(t)\\[1ex]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57257de520512a5d4eeb5260f888646942fa5d89)