Вписанный четырехугольник

Четырехугольник, все вершины которого могут принадлежать одной окружности

В евклидовой геометрии вписанный четырехугольник или вписанный четырехугольник — это четырехугольник , все вершины которого лежат на одной окружности . Эта окружность называется описанной окружностью или описанным кругом , а вершины называются конциклическими . Центр окружности и ее радиус называются центром описанной окружности и радиусом описанной окружности соответственно. Другие названия для этих четырехугольников — конциклический четырехугольник и хордальный четырехугольник , последнее из которых связано с тем, что стороны четырехугольника являются хордами описанной окружности. Обычно четырехугольник предполагается выпуклым , но существуют также скрещенные вписанные четырехугольники. Формулы и свойства, приведенные ниже, справедливы и в выпуклом случае.

Слово «циклический» происходит от древнегреческого κύκλος ( куклос ), что означает «круг» или «колесо».

Все треугольники имеют описанную окружность , но не все четырехугольники имеют. Примером четырехугольника, который не может быть вписанным, является неквадратный ромб . В характеристиках раздела ниже указано, каким необходимым и достаточным условиям должен удовлетворять четырехугольник, чтобы иметь описанную окружность.

Особые случаи

Любой квадрат , прямоугольник , равнобедренная трапеция или антипараллелограмм являются вписанными. Воздушный змей является вписанным тогда и только тогда, когда у него есть два прямых угла – прямой змей . Вписанно-описанным четырёхугольником является вписанный четырёхугольник, который также является касательным , а вписанно-описанным четырёхугольником является вписанный четырёхугольник, который также является вписанным . Гармонический четырёхугольник – это вписанный четырёхугольник, в котором произведения длин противоположных сторон равны.

Характеристика

Окружнойцентр

Выпуклый четырехугольник является вписанным тогда и только тогда, когда четыре перпендикуляра к сторонам пересекаются . Эта общая точка является центром описанной окружности . ^[1]

Дополнительные углы

Выпуклый четырехугольник $ABCD$ является вписанным тогда и только тогда, когда его противолежащие углы являются дополнительными , то есть ^[1]^[2]

\альфа +\гамма =\бета +\дельта =\пи \ {\text{радианы}}\ (=180^{\circ }).

Прямая теорема была утверждением 22 в третьей книге « Начал » Евклида . [ ^3] Эквивалентно, выпуклый четырехугольник является вписанным тогда и только тогда, когда каждый внешний угол равен противолежащему внутреннему углу .

В 1836 году Дункан Грегори обобщил этот результат следующим образом: для любого выпуклого вписанного 2 n -угольника две суммы внутренних чередующихся углов равны ( n -1) . ^[4] Этот результат можно обобщить следующим образом: если A1A2...A2n (n > 1) — любой вписанный 2 n -угольник, в котором вершина Ai->Ai+k (вершина Ai соединена с Ai+k ), то две суммы внутренних чередующихся углов равны m (где m = n — k, а k = 1, 2, 3, ... — полный поворот). ^[5] $\пи$ $\пи$

Взяв стереографическую проекцию (тангенс половинного угла) каждого угла, это можно переформулировать,

{\frac {\tan {\frac {\alpha }{2}}+\tan {\frac {\gamma }{2}}}{1-\tan {\frac {\alpha }{2} }\tan {\frac {\gamma }{2}}}}={\frac {\tan {\frac {\beta }{2}}+\tan {\frac {\delta }{2}}}{1-\tan {\frac {\beta }{2}}\tan {\frac {\delta }{2}}}}=\infty .

Что подразумевает, что ^[6]

\tan {\frac {\alpha }{2}}\tan {\frac {\gamma }{2}}=\tan {\frac {\beta }{2}}{\tan {\frac { \дельта {2}}}=1

Углы между сторонами и диагоналями

Выпуклый четырехугольник $ABCD$ является вписанным тогда и только тогда, когда угол между стороной и диагональю равен углу между противолежащей стороной и другой диагональю. ^[7] То есть, например,

\угол ACB=\угол ADB.

Паскаль баллы

{\displaystyle \омега} — *ABCD* — вписанный четырёхугольник. E — точка пересечения диагоналей, а F — точка пересечения продолжений сторон BC и AD . — окружность, диаметр которой — отрезок EF . P и Q — точки Паскаля, образованные окружностью . Треугольники *FAB* и *FCD* подобны. $\омега$ $\омега$

Другие необходимые и достаточные условия для того, чтобы выпуклый четырехугольник $ABCD$ был вписанным, таковы: пусть $E$ — точка пересечения диагоналей, пусть $F$ — точка пересечения продолжений сторон $AD$ и $BC$ , пусть — окружность, диаметр которой — отрезок $EF$ , и пусть $P$ и $Q$ — точки Паскаля на сторонах $AB$ и $CD,$ образованных окружностью . (1) $ABCD$ является вписанным четырехугольником тогда и только тогда, когда точки $P$ и $Q$ лежат на одной прямой с центром $O$ окружности . (2) $ABCD$ является вписанным четырехугольником тогда и только тогда, когда точки $P$ и $Q$ являются серединами сторон $AB$ и $CD$ . ^[2] $\омега$ $\омега$
$\омега$

Пересечение диагоналей

Если две прямые, одна из которых содержит отрезок $AC$ , а другая содержит отрезок $BD$ , пересекаются в точке $E$ , то четыре точки $A$ , $B$ , $C$ , $D$ лежат на одной окружности тогда и только тогда, когда ^[8]

\displaystyle AE\cdot EC=BE\cdot ED.

Пересечение $E$ может быть внутренним или внешним по отношению к окружности. В первом случае вписанный четырехугольник — это $ABCD$ , а во втором случае вписанный четырехугольник — это $ABDC$ . Когда пересечение внутреннее, равенство утверждает, что произведение длин отрезков, на которые $E$ делит одну диагональ, равно произведению длин другой диагонали. Это известно как теорема о пересекающихся хордах , поскольку диагонали вписанного четырехугольника являются хордами описанной окружности.

Теорема Птолемея

Теорема Птолемея выражает произведение длин двух диагоналей $e$ и $f$ вписанного четырехугольника как равное сумме произведений противоположных сторон: ^[9]^{: стр.25}^[2]

\displaystyle ef=ac+bd,

где a , b , c , d — длины сторон в порядке возрастания. Обратное также верно. То есть, если это уравнение выполняется в выпуклом четырехугольнике, то образуется вписанный четырехугольник.

Диагональный треугольник

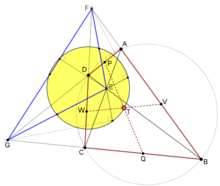
В выпуклом четырехугольнике $ABCD$ пусть $EFG$ — диагональный треугольник $ABCD$ , а — окружность девяти точек $EFG$ . $ABCD$ является вписанным тогда и только тогда, когда точка пересечения бимедиан $ABCD$ принадлежит окружности девяти точек . ^[10]^[11]^[2] $\омега$ $\омега$

Область

Площадь K вписанного четырехугольника со сторонами $a$ , $b$ , $c$ , $d$ определяется формулой Брахмагупты ^[9] $:$ ^стр.24

{\ displaystyle K = {\ sqrt {(sa) (sb) (sc) (sd)}} \,}

где $s$ , полупериметр , равен $s = ⁠ 1 / 2 ⁠ (a + b + c + d)$ . Это следствие формулы Бретшнайдера дляобщего четырехугольника, поскольку противолежащие углы являются дополнительными в случае вписанного четырехугольника. Если также $d = 0$ , вписанный четырехугольник становится треугольником и формула сводится к формуле Герона .

Вписанный четырехугольник имеет максимальную площадь среди всех четырехугольников с одинаковыми длинами сторон (независимо от последовательности). Это еще одно следствие формулы Бретшнайдера. Это также можно доказать с помощью исчисления . ^[12]

Четыре неравные длины, каждая из которых меньше суммы трех других, являются сторонами каждого из трех неконгруэнтных вписанных четырехугольников, ^[13] которые по формуле Брахмагупты все имеют одинаковую площадь. В частности, для сторон $a$ , $b$ , $c$ , и $d$ , сторона $a$ может быть противоположна любой из сторон $b$ , стороны $c$ , или стороны $d$ .

Площадь вписанного четырехугольника с последовательными сторонами $a$ , $b$ , $c$ , $d$ , углом $A$ между сторонами $a$ и $d$ и углом $B$ между сторонами $a$ и $b$ можно выразить как ^[9]^{: стр.25}

K={\tfrac {1}{2}}(ab+cd)\sin {B}

или

K={\tfrac {1}{2}}(ad+bc)\sin {A}

или ^[9]^{: стр.26}

K={\tfrac {1}{2}}(ac+bd)\sin {\theta }

где $θ$ — это любой из углов между диагоналями. При условии, что $A$ — не прямой угол, площадь также может быть выражена как ^[9]^{: стр.26}

K={\tfrac {1}{4}}(a^{2}-b^{2}-c^{2}+d^{2})\tan {A}.

Другая формула ^[14]^{: стр.83}

\displaystyle K=2R^{2}\sin {A}\sin {B}\sin {\theta }

где $R$ — радиус описанной окружности . Как прямое следствие, ^[15]

K\leq 2R^{2}

где равенство имеет место тогда и только тогда, когда четырехугольник является квадратом.

Диагонали

Во вписанном четырехугольнике с последовательными вершинами $A$ , $B$ , $C$ , $D$ и сторонами $a = AB$ , $b = BC$ , $c = CD$ и $d = DA$ длины диагоналей $p = AC$ и $q = BD$ можно выразить через стороны следующим образом: ^[9]^{: стр. 25,}^[16]^[17]^{: стр. 84}

p={\sqrt {\frac {(ac+bd)(ad+bc)}{ab+cd}}}

и

q={\sqrt {\frac {(ac+bd)(ab+cd)}{ad+bc}}}

так показывая теорему Птолемея

pq=ac+bd.

Согласно второй теореме Птолемея , ^[9]^{: стр.25,}^[16]

{\frac {p}{q}}={\frac {ad+bc}{ab+cd}}

используя те же обозначения, что и выше.

Для суммы диагоналей имеем неравенство ^[18]^{: стр.123, №2975}

p+q\geq 2{\sqrt {ac+bd}}.

Равенство имеет место тогда и только тогда, когда диагонали имеют одинаковую длину, что можно доказать с помощью неравенства AM-GM .

Более того, ^[18]^{: стр.64, №1639}

(p+q)^{2}\leq (a+c)^{2}+(b+d)^{2}.

В любом выпуклом четырехугольнике две диагонали вместе разбивают четырехугольник на четыре треугольника; во вписанном четырехугольнике противолежащие пары этих четырех треугольников подобны друг другу.

Если $ABCD$ — вписанный четырехугольник, в котором $AC$ пересекает $BD$ в точке $E$ , то ^[19]

{\frac {AE}{CE}}={\frac {AB}{CB}}\cdot {\frac {AD}{CD}}.

Набор сторон, которые могут образовывать циклический четырехугольник, может быть расположен в любой из трех различных последовательностей, каждая из которых может образовывать циклический четырехугольник той же площади в той же описанной окружности (площади одинаковы согласно формуле площади Брахмагупты). Любые два из этих циклических четырехугольников имеют одну общую диагональную длину. ^[17]^{: стр. 84}

Формулы угла

Для вписанного четырехугольника с последовательными сторонами $a$ $,$ b $,$ c $,$ d $,$ полупериметром s $и$ углом $A$ между сторонами $a$ и $d$ тригонометрические функции A задаются формулой ^[20]

\cos A={\frac {a^{2}-b^{2}-c^{2}+d^{2}}{2(ad+bc)}},

\sin A={\frac {2{\sqrt {(sa)(sb)(sc)(sd)}}}{(ad+bc)}},

\tan {\frac {A}{2}}={\sqrt {\frac {(sa)(sd)}{(sb)(sc)}}}.

Угол $θ$ между диагоналями, противолежащими сторонам $a$ и $c,$ удовлетворяет ^[9]^{: стр.26}

\tan {\frac {\theta }{2}}={\sqrt {\frac {(sb)(sd)}{(sa)(sc)}}}.

Если продолжения противоположных сторон $a$ и $c$ пересекаются под углом $φ$ , то

\cos {\frac {\varphi}{2}}={\sqrt {\frac {(sb)(sd)(b+d)^{2}}{(ab+cd)(ad+bc)}}}

где $s$ — полупериметр . ^[9]^{: стр.31}

Пусть обозначим угол между сторонами и , угол между и , а также угол между и , тогда: ^[21] $Б$ $а$ $б$ $С$ $б$ $с$ $D$ $с$ $д$

{\begin{aligned}{\frac {a+c}{b+d}}&={\frac {\sin {\tfrac {1}{2}}(A+B)}{\cos {\tfrac {1}{2}}(C-D)}}\tan {\tfrac {1}{2}}\theta ,\\[10mu]{\frac {a-c}{b-d}}&={\frac {\cos {\tfrac {1}{2}}(A+B)}{\sin {\tfrac {1}{2}}(D-C)}}\cot {\tfrac {1}{2}}\theta .\end{aligned}}

Формула радиуса описанной окружности Парамешвары

Вписанный четырехугольник с последовательными сторонами $a$ , $b$ , $c$ , $d$ и полупериметром $s$ имеет радиус описанной окружности , заданный формулой [ ^16]^[22]

R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}}.

Это было выведено индийским математиком Ватассери Парамешварой в 15 веке. (Обратите внимание, что радиус инвариантен при перестановке длин любых сторон.)

Используя формулу Брахмагупты , формулу Парамешвары можно переформулировать так:

4KR={\sqrt {(ab+cd)(ac+bd)(ad+bc)}}

где $K$ — площадь вписанного четырехугольника.

Антицентр и коллинеарности

Четыре отрезка, каждый из которых перпендикулярен одной стороне вписанного четырехугольника и проходит через середину противоположной стороны , являются конкурирующими . ^[23]^{: стр. 131,}^[24] Эти отрезки называются малтидами , ^[25] что является сокращением от высоты срединной точки. Их общая точка называется антицентром . Она обладает свойством быть отражением центра описанной окружности относительно «вершинного центроида» . Таким образом, во вписанном четырехугольнике центр описанной окружности, «вершинный центроид» и антицентр являются коллинеарными . ^[24]

Если диагонали вписанного четырехугольника пересекаются в точке $P$ , а середины диагоналей — M $и$ N $,$ то антицентр четырехугольника является ортоцентром треугольника $MNP$ .

Антицентр вписанного четырехугольника — это точка Понселе его вершин.

Другие свойства

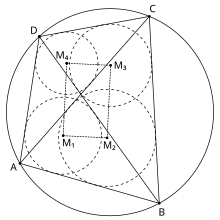
В вписанном четырехугольнике $ABCD$ инцентры M ₁ , M ₂ , M ₃ , M ₄ (см. рисунок справа) в треугольниках $DAB$ , $ABC$ , $BCD$ и $CDA$ являются вершинами прямоугольника . Это одна из теорем, известных как японская теорема . Ортоцентры тех же четырех треугольников являются вершинами четырехугольника, $конгруэнтного ABCD$ , а центроиды в этих четырех треугольниках являются вершинами другого вписанного четырехугольника. ^[7]
Во вписанном четырехугольнике $ABCD$ с центром описанной окружности $O$ пусть $P$ — точка пересечения диагоналей $AC$ и $BD$ . Тогда угол $APB$ является средним арифметическим углов $AOB$ и $COD$ . Это прямое следствие теоремы о вписанном угле и теоремы о внешнем угле .
Не существует вписанных четырехугольников с рациональной площадью и неравными рациональными сторонами ни в арифметической , ни в геометрической прогрессии . ^[26]

Если вписанный четырехугольник имеет длины сторон, образующие арифметическую прогрессию, то такой четырехугольник также является вписанно-бицентрическим .
Если противоположные стороны вписанного четырехугольника продолжить до точки $E$ и $F$ , то внутренние биссектрисы углов $E$ и $F$ будут перпендикулярны. ^[13]

Четырехугольники Брахмагупты

Четырехугольник Брахмагупты ^[27] — это вписанный четырехугольник с целыми сторонами, целыми диагоналями и целой площадью. Все четырехугольники Брахмагупты со сторонами $a$ , $b$ , $c$ , $d$ , диагоналями $e$ , $f$ , площадью $K$ и радиусом описанной окружности $R$ можно получить, очистив знаменатели из следующих выражений, содержащих рациональные параметры $t$ , $u$ и $v$ :

a=[t(u+v)+(1-uv)][u+v-t(1-uv)]

b=(1+u^{2})(v-t)(1+tv)

c=t(1+u^{2})(1+v^{2})

d=(1+v^{2})(u-t)(1+tu)

e=u(1+t^{2})(1+v^{2})

f=v(1+t^{2})(1+u^{2})

K=uv[2t(1-uv)-(u+v)(1-t^{2})][2(u+v)t+(1-uv)(1-t^{2})]

4R=(1+u^{2})(1+v^{2})(1+t^{2}).

Ортодиагональный случай

Радиус описанной окружности и площадь

Для вписанного четырехугольника, который также является ортодиагональным (имеет перпендикулярные диагонали), предположим, что пересечение диагоналей делит одну диагональ на отрезки длиной $p 1$ и $p 2$ и делит другую диагональ на отрезки длиной $q 1$ и $q 2.$ Тогда ^[28] (первое равенство — это предложение 11 в Книге лемм Архимеда )

D^{2}=p_{1}^{2}+p_{2}^{2}+q_{1}^{2}+q_{2}^{2}=a^{2}+c^{2}=b^{2}+d^{2}

где $D$ — диаметр описанной окружности . Это справедливо, поскольку диагонали являются перпендикулярными хордами окружности . Эти уравнения подразумевают, что радиус описанной окружности $R$ может быть выражен как

R={\tfrac {1}{2}}{\sqrt {p_{1}^{2}+p_{2}^{2}+q_{1}^{2}+q_{2}^{2}}}

или, в терминах сторон четырехугольника, как ^[23]

R={\tfrac {1}{2}}{\sqrt {a^{2}+c^{2}}}={\tfrac {1}{2}}{\sqrt {b^{2}+d^{2}}}.

Из этого также следует, что ^[23]

a^{2}+b^{2}+c^{2}+d^{2}=8R^{2}.

Таким образом, согласно теореме Эйлера о четырехугольнике , радиус описанной окружности можно выразить через диагонали $p$ и $q$ , а расстояние $x$ между серединами диагоналей — как

R={\sqrt {\frac {p^{2}+q^{2}+4x^{2}}{8}}}.

Формула для площади $K$ вписанного ортодиагонального четырехугольника через четыре стороны получается непосредственно при объединении теоремы Птолемея и формулы для площади ортодиагонального четырехугольника . Результат ^[29]^{: стр.222}

K={\tfrac {1}{2}}(ac+bd).

Другие свойства

В вписанном ортодиагональном четырехугольнике антицентр совпадает с точкой пересечения диагоналей. ^[23]
Теорема Брахмагупты утверждает, что для вписанного четырехугольника, который также является ортодиагональным , перпендикуляр с любой стороны через точку пересечения диагоналей делит противоположную сторону пополам. ^[23]
Если вписанный четырехугольник также является ортодиагональным, то расстояние от центра описанной окружности до любой стороны равно половине длины противоположной стороны. ^[23]
В вписанном ортодиагональном четырехугольнике расстояние между серединами диагоналей равно расстоянию между центром описанной окружности и точкой пересечения диагоналей. ^[23]

Вписанные сферические четырехугольники

В сферической геометрии сферический четырехугольник, образованный четырьмя пересекающимися большими окружностями, является вписанным тогда и только тогда, когда суммы противолежащих углов равны, т. е. α + γ = β + δ для последовательных углов α, β, γ, δ четырехугольника. ^[30] Одно направление этой теоремы было доказано Андерсом Йоханом Лекселлем в 1782 году . ^[31] Лекселл показал, что в сферическом четырехугольнике, вписанном в малый круг сферы, суммы противолежащих углов равны, а в описанном четырехугольнике суммы противолежащих сторон равны. Первая из этих теорем является сферическим аналогом теоремы о плоскости, а вторая теорема является ее двойственной, то есть результатом перестановки больших окружностей и их полюсов. ^[32] Кипер и др. ^[33] доказали обратную теорему: если в сферическом четырехугольнике суммы противоположных сторон равны, то для этого четырехугольника существует вписанная окружность.

Смотрите также

Ссылки

^ ab Usiskin, Zalman; Griffin, Jennifer; Witonsky, David; Willmore, Edwin (2008), "10. Вписанные четырехугольники", Классификация четырехугольников: исследование определения , Исследования в области математического образования, IAP, стр. 63–65 , ISBN 978-1-59311-695-8
^ abcd Фрайверт, Дэвид; Сиглер, Ави; Ступель, Моше (2020), «Необходимые и достаточные свойства вписанного четырехугольника», Международный журнал математического образования в науке и технике , 51 (6): 913–938 , doi :10.1080/0020739X.2019.1683772, S2CID 209930435
↑ Джойс, Д.Э. (июнь 1997 г.), «Книга 3, Предложение 22», «Начала Евклида » , Университет Кларка
↑ Грегори, Дункан (1836), «Геометрическая теорема», Cambridge Mathematical Journal , 1 : 92.
^ Де Вильерс, Майкл (1993), «Объединяющее обобщение теоремы Тернбулла», Международный журнал математического образования в науке и технике , 24 (2): 191– 196, doi :10.1080/0020739930240204.
^ Хаджа, Моваффак (2008), «Условие для того, чтобы описанный четырехугольник был вписанным» (PDF) , Forum Geometricorum , 8 : 103–6 , архивировано из оригинала (PDF) 26 ноября 2019 г. , извлечено 16 августа 2011 г.
^ аб Андрееску, Титу; Энеску, Богдан (2004), «2.3 Циклические четверные», Сокровища математической олимпиады, Springer, стр. 44–46, 50, ISBN 978-0-8176-4305-8, МР 2025063
^ Брэдли, Кристофер Дж. (2007), Алгебра геометрии: декартовы, ареальные и проективные координаты , Highperception, стр. 179, ISBN 978-1906338008, OCLC 213434422
^ abcdefghi Дарелл, CV; Робсон, А. (2003) [1930], Расширенная тригонометрия, Courier Dover, ISBN 978-0-486-43229-8
^ Фрайверт, Дэвид (июль 2019 г.). «Новые точки, принадлежащие девятиточечной окружности». The Mathematical Gazette . 103 (557): 222– 232. doi :10.1017/mag.2019.53.
^ Фрайверт, Дэвид (2018). «Новые приложения метода комплексных чисел в геометрии вписанных четырехугольников» (PDF) . Международный журнал геометрии . 7 (1): 5–16 .
↑ Питер, Томас (сентябрь 2003 г.), «Максимизация площади четырехугольника», The College Mathematics Journal , 34 (4): 315– 6, doi : 10.2307/3595770, JSTOR 3595770
^ ab Coxeter, Harold Scott MacDonald; Greitzer, Samuel L. (1967), "3.2 Циклические четырехугольники; формула Брахмагупты", Geometry Revisited , Mathematical Association of America, стр. 57, 60, ISBN 978-0-88385-619-2
^ Прасолов, Виктор, Задачи по плоской и стереометрии: т. 1 Plane Geometry (PDF) , архивировано из оригинала (PDF) 21 сентября 2018 г. , извлечено 6 ноября 2011 г.
^ Альсина, Клауди; Нельсен, Роджер (2009), «4.3 Циклические, тангенциальные и бицентрические четырехугольники», Когда меньше значит больше: Визуализация основных неравенств, Математическая ассоциация Америки, стр. 64, ISBN 978-0-88385-342-9
^ abc Alsina, Claudi; Nelsen, Roger B. (2007), «О диагоналях вписанного четырехугольника» (PDF) , Forum Geometricorum , 7 : 147–9
^ Джонсон, Роджер А., Продвинутая евклидова геометрия , Dover Publ., 2007 (ориг. 1929).
^ ab Неравенства, предложенные в « Crux Mathematicorum » , 2007, [1].
^ А. Богомольный , Тождество в (циклических) четырехугольниках, Interactive Mathematics Miscellany and Puzzles , [2], Доступ 18 марта 2014 г.
^ Сиддонс, AW; Хьюз, RT (1929), Тригонометрия , Cambridge University Press, стр. 202, OCLC 429528983
^ Хосе Гарсия, Эммануэль Антонио (2022), «Обобщение формулы Мольвейде (скорее Ньютона)» (PDF) , Matinf , 5 ( 9– 10): 19– 22 , получено 29 декабря 2023 г.
↑ Хоэн, Ларри (март 2000 г.), «Описанная окружность вписанного четырехугольника», Mathematical Gazette , 84 (499): 69– 70, doi : 10.2307/3621477, JSTOR 3621477
^ abcdefg Альтшиллер-Корт, Натан (2007) [1952], Геометрия колледжа: Введение в современную геометрию треугольника и окружности (2-е изд.), Courier Dover, стр. 131, 137–8 , ISBN 978-0-486-45805-2, OCLC 78063045
^ ab Honsberger, Ross (1995), "4.2 Циклические четырехугольники", Эпизоды в евклидовой геометрии девятнадцатого и двадцатого века , Новая математическая библиотека, т. 37, Cambridge University Press, стр. 35–39 , ISBN 978-0-88385-639-0
^ Вайсштейн, Эрик В. «Мальтити». Математический мир .
^ Бухгольц, Р. Х.; Макдугалл, Дж. А. (1999), «Четырехугольники Герона со сторонами в арифметической или геометрической прогрессии», Бюллетень Австралийского математического общества , 59 (2): 263– 9, doi : 10.1017/S0004972700032883 , hdl : 1959.13/803798 , MR 1680787
^ Sastry, KRS (2002). «Brahmagupta fourilaterals» (PDF) . Forum Geometricorum . 2 : 167– 173. Архивировано из оригинала (PDF) 22 апреля 2018 г. . Получено 25 апреля 2012 г. .
^ Посаментье, Альфред С.; Салкинд, Чарльз Т. (1970), «Решения: 4-23 Докажите, что сумма квадратов мер отрезков, образованных двумя перпендикулярными хордами, равна квадрату меры диаметра данной окружности». Сложные задачи по геометрии (2-е изд.), Courier Dover, стр. 104–5, ISBN 978-0-486-69154-1
^ Йозефссон, Мартин (2016), «Свойства пифагорейских четырехугольников», The Mathematical Gazette , 100 (июль): 213–224 , doi :10.1017/mag.2016.57.
^ Виммер, Линхард (2011). «Циклические многоугольники в неевклидовой геометрии». Элементы математики . 66 (2): 74–82 . doi : 10.4171/EM/173 .
^ Лекселл, Андерс Йохан (1786). «De proprietatibus circulorum in superficie sphaerica descriptorum». Acta Academiae Scientiarum Imperialis Petropolitanae . 6 : 1782 (1): 58–103 , табл. с рисунками. 3.
^ Rosenfeld, BA (1988). История неевклидовой геометрии - Springer . Исследования по истории математики и физических наук. Том 12. doi :10.1007/978-1-4419-8680-1. ISBN 978-1-4612-6449-1.
^ Кипер, Гёкхан; Сёйлемез, Эрес (1 мая 2012 г.). «Гомотетические связи, подобные джиттербагу». Теория механизмов и машин . 51 : 145–158 . doi :10.1016/j.mechmachtheory.2011.11.014.

Дальнейшее чтение

D. Fraivert: Четырехугольники с точками Паскаля, вписанные во вписанный четырехугольник

Внешние ссылки

Вывод формулы площади вписанного четырехугольника
Центры вписанных окружностей в четырехугольнике в точке разрезания узла
Четыре параллельные линии во вписанном четырехугольнике в точке разрезания узла
Вайсштейн, Эрик В. "Вписанный четырехугольник". MathWorld .

[Usiskin-1] Usiskin, Zalman; Griffin, Jennifer; Witonsky, David; Willmore, Edwin (2008), "10. Вписанные четырехугольники", Классификация четырехугольников: исследование определения , Исследования в области математического образования, IAP, стр. 63–65 , ISBN 978-1-59311-695-8

[Fraivert-2] Фрайверт, Дэвид; Сиглер, Ави; Ступель, Моше (2020), «Необходимые и достаточные свойства вписанного четырехугольника», Международный журнал математического образования в науке и технике , 51 (6): 913–938 , doi :10.1080/0020739X.2019.1683772, S2CID 209930435

[3] Джойс, Д.Э. (июнь 1997 г.), «Книга 3, Предложение 22», «Начала Евклида » , Университет Кларка

[4] Грегори, Дункан (1836), «Геометрическая теорема», Cambridge Mathematical Journal , 1 : 92.

[5] Де Вильерс, Майкл (1993), «Объединяющее обобщение теоремы Тернбулла», Международный журнал математического образования в науке и технике , 24 (2): 191– 196, doi :10.1080/0020739930240204.

[6] Хаджа, Моваффак (2008), «Условие для того, чтобы описанный четырехугольник был вписанным» (PDF) , Forum Geometricorum , 8 : 103–6 , архивировано из оригинала (PDF) 26 ноября 2019 г. , извлечено 16 августа 2011 г.

[Andreescu-7] аб Андрееску, Титу; Энеску, Богдан (2004), «2.3 Циклические четверные», Сокровища математической олимпиады, Springer, стр. 44–46, 50, ISBN 978-0-8176-4305-8, МР 2025063

[8] Брэдли, Кристофер Дж. (2007), Алгебра геометрии: декартовы, ареальные и проективные координаты , Highperception, стр. 179, ISBN 978-1906338008, OCLC 213434422

[Durell-9] Дарелл, CV; Робсон, А. (2003) [1930], Расширенная тригонометрия, Courier Dover, ISBN 978-0-486-43229-8

[10] Фрайверт, Дэвид (июль 2019 г.). «Новые точки, принадлежащие девятиточечной окружности». The Mathematical Gazette . 103 (557): 222– 232. doi :10.1017/mag.2019.53.

[11] Фрайверт, Дэвид (2018). «Новые приложения метода комплексных чисел в геометрии вписанных четырехугольников» (PDF) . Международный журнал геометрии . 7 (1): 5–16 .

[12] Питер, Томас (сентябрь 2003 г.), «Максимизация площади четырехугольника», The College Mathematics Journal , 34 (4): 315– 6, doi : 10.2307/3595770, JSTOR 3595770

[Coxeter-13] Coxeter, Harold Scott MacDonald; Greitzer, Samuel L. (1967), "3.2 Циклические четырехугольники; формула Брахмагупты", Geometry Revisited , Mathematical Association of America, стр. 57, 60, ISBN 978-0-88385-619-2

[14] Прасолов, Виктор, Задачи по плоской и стереометрии: т. 1 Plane Geometry (PDF) , архивировано из оригинала (PDF) 21 сентября 2018 г. , извлечено 6 ноября 2011 г.

[Alsina-15] Альсина, Клауди; Нельсен, Роджер (2009), «4.3 Циклические, тангенциальные и бицентрические четырехугольники», Когда меньше значит больше: Визуализация основных неравенств, Математическая ассоциация Америки, стр. 64, ISBN 978-0-88385-342-9

[Alsina2-16] Alsina, Claudi; Nelsen, Roger B. (2007), «О диагоналях вписанного четырехугольника» (PDF) , Forum Geometricorum , 7 : 147–9

[Johnson-17] Джонсон, Роджер А., Продвинутая евклидова геометрия , Dover Publ., 2007 (ориг. 1929).

[Crux-18] Неравенства, предложенные в « Crux Mathematicorum » , 2007, [1].

[19] А. Богомольный , Тождество в (циклических) четырехугольниках, Interactive Mathematics Miscellany and Puzzles , [2], Доступ 18 марта 2014 г.

[20] Сиддонс, AW; Хьюз, RT (1929), Тригонометрия , Cambridge University Press, стр. 202, OCLC 429528983

[21] Хосе Гарсия, Эммануэль Антонио (2022), «Обобщение формулы Мольвейде (скорее Ньютона)» (PDF) , Matinf , 5 ( 9– 10): 19– 22 , получено 29 декабря 2023 г.

[22] Хоэн, Ларри (март 2000 г.), «Описанная окружность вписанного четырехугольника», Mathematical Gazette , 84 (499): 69– 70, doi : 10.2307/3621477, JSTOR 3621477

[Altshiller-Court-23] Альтшиллер-Корт, Натан (2007) [1952], Геометрия колледжа: Введение в современную геометрию треугольника и окружности (2-е изд.), Courier Dover, стр. 131, 137–8 , ISBN 978-0-486-45805-2, OCLC 78063045

[Honsberger-24] Honsberger, Ross (1995), "4.2 Циклические четырехугольники", Эпизоды в евклидовой геометрии девятнадцатого и двадцатого века , Новая математическая библиотека, т. 37, Cambridge University Press, стр. 35–39 , ISBN 978-0-88385-639-0

[25] Вайсштейн, Эрик В. «Мальтити». Математический мир .

[Buchholz-26] Бухгольц, Р. Х.; Макдугалл, Дж. А. (1999), «Четырехугольники Герона со сторонами в арифметической или геометрической прогрессии», Бюллетень Австралийского математического общества , 59 (2): 263– 9, doi : 10.1017/S0004972700032883 , hdl : 1959.13/803798 , MR 1680787

[27] Sastry, KRS (2002). «Brahmagupta fourilaterals» (PDF) . Forum Geometricorum . 2 : 167– 173. Архивировано из оригинала (PDF) 22 апреля 2018 г. . Получено 25 апреля 2012 г. .

[28] Посаментье, Альфред С.; Салкинд, Чарльз Т. (1970), «Решения: 4-23 Докажите, что сумма квадратов мер отрезков, образованных двумя перпендикулярными хордами, равна квадрату меры диаметра данной окружности». Сложные задачи по геометрии (2-е изд.), Courier Dover, стр. 104–5, ISBN 978-0-486-69154-1

[29] Йозефссон, Мартин (2016), «Свойства пифагорейских четырехугольников», The Mathematical Gazette , 100 (июль): 213–224 , doi :10.1017/mag.2016.57.

[30] Виммер, Линхард (2011). «Циклические многоугольники в неевклидовой геометрии». Элементы математики . 66 (2): 74–82 . doi : 10.4171/EM/173 .

[31] Лекселл, Андерс Йохан (1786). «De proprietatibus circulorum in superficie sphaerica descriptorum». Acta Academiae Scientiarum Imperialis Petropolitanae . 6 : 1782 (1): 58–103 , табл. с рисунками. 3.

[32] Rosenfeld, BA (1988). История неевклидовой геометрии - Springer . Исследования по истории математики и физических наук. Том 12. doi :10.1007/978-1-4419-8680-1. ISBN 978-1-4612-6449-1.

[33] Кипер, Гёкхан; Сёйлемез, Эрес (1 мая 2012 г.). «Гомотетические связи, подобные джиттербагу». Теория механизмов и машин . 51 : 145–158 . doi :10.1016/j.mechmachtheory.2011.11.014.