Слияние (реферативная переписка)
Название «слияние» взято из географии, где оно означает место встречи двух водоемов.

В информатике и математике слияние — это свойство систем переписывания , описывающее, какие термины в такой системе могут быть переписаны более чем одним способом, чтобы получить тот же результат. В этой статье описываются свойства в наиболее абстрактной обстановке абстрактной системы переписывания .

Мотивирующие примеры

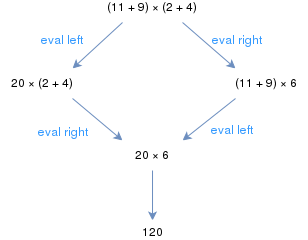
Обычные правила элементарной арифметики образуют абстрактную систему переписывания. Например, выражение (11 + 9) × (2 + 4) может быть оценено, начиная как с левой, так и с правой скобки; однако в обоих случаях в конечном итоге получается один и тот же результат. Если каждое арифметическое выражение оценивается с одним и тем же результатом независимо от стратегии сокращения, арифметическая система переписывания называется базисно-конфлюэнтной. Арифметические системы переписывания могут быть конфлюэнтными или только базисно-конфлюэнтными в зависимости от деталей системы переписывания. [1]

Второй, более абстрактный пример получается из следующего доказательства того, что каждый элемент группы равен обратному своему обратному элементу: [2]

Групповые аксиомы
А11 ⋅ а= а
А2а −1 ⋅ а= 1
А3    ( а ⋅ б ) ⋅ в= а ⋅ ( б ⋅ в )
Доказательство R4 : a −1 ⋅( a ⋅ b ) = b
а −1 ⋅ ( а ⋅ б )
=( а −1 ⋅ а ) ⋅ бпо А3(р)    
=1 ⋅ бот А2
=бот А1
Доказательство R6 : ( a −1 ) −1 ⋅ 1 = a
( а −1 ) −1 ⋅ 1
=( а −1 ) −1 ⋅ ( а −1 ⋅ а )по А2(р)
=аот R4
Доказательство R10 : ( a −1 ) −1 ⋅ b = a ⋅ b
( а −1 ) −1 ⋅ б
=( а −1 ) −1 ⋅ ( а −1 ⋅ ( а ⋅ б ))по R4(r)
=а ⋅ бот R4
Доказательство R11 : a ⋅ 1 = a
а ⋅ 1
=( а −1 ) −1 ⋅ 1по R10(р)
=аот R6
Доказательство R12 : ( a −1 ) −1 = a
( а −1 ) −1
=( а −1 ) −1 ⋅ 1по R11(р)    
=аот R6

Это доказательство начинается с заданных групповых аксиом A1–A3 и устанавливает пять предложений R4, R6, R10, R11 и R12, каждое из которых использует некоторые более ранние, а R12 является основной теоремой. Некоторые из доказательств требуют неочевидных или даже творческих шагов, таких как применение аксиомы A2 в обратном порядке, тем самым переписывая «1» в « a −1 ⋅ a» на первом шаге доказательства R6. Одной из исторических мотиваций для разработки теории переписывания терминов было избежание необходимости в таких шагах, которые трудно найти неопытному человеку, не говоря уже о компьютерной программе [ требуется цитата ] .

Если система переписывания терминов является конфлюэнтной и завершающейся , существует простой метод доказательства равенства между двумя выражениями (также известными как термины ) s и t : начиная с s , применяйте равенства [примечание 1] слева направо как можно дольше, в конечном итоге получая термин s′ . Получите из t термин t′ аналогичным образом. Если оба термина s′ и t′ буквально совпадают, то доказано, что s и t равны. Что еще более важно, если они не совпадают, то s и t не могут быть равны. То есть любые два термина s и t , равенство которых вообще может быть доказано, можно сделать этим методом.

Успех этого метода не зависит от определенного сложного порядка применения правил переписывания, поскольку слияние гарантирует, что любая последовательность применения правил в конечном итоге приведет к одному и тому же результату (в то время как свойство завершения гарантирует, что любая последовательность в конечном итоге достигнет конца). Следовательно, если для некоторой эквациональной теории может быть предоставлена ​​конфлюэнтная и завершающая система переписывания терминов , [примечание 2] не требуется ни капли креативности для выполнения доказательств равенства терминов; эта задача, следовательно, становится поддающейся компьютерным программам. Современные подходы обрабатывают более общие абстрактные системы переписывания, а не системы переписывания терминов ; последние являются частным случаем первых.

Общий случай и теория

На этой диаграмме a сводится к b или c за ноль или более шагов перезаписи (обозначенных звездочкой). Для того чтобы отношение перезаписи было конфлюэнтным, оба редукта должны в свою очередь свестись к некоторому общему d .

Система переписывания может быть выражена как направленный граф , в котором узлы представляют выражения, а ребра представляют переписывания. Так, например, если выражение a можно переписать в b , то мы говорим, что b является сокращением a (альтернативно, a сводится к b , или a является расширением b ). Это представлено с помощью стрелочной нотации; a → b указывает , что a сводится к b . Интуитивно это означает, что соответствующий граф имеет направленное ребро от a к b .

Если существует путь между двумя узлами графа c и d , то он образует последовательность сокращения . Так, например, если c → c′ → c′′ → ... → d′ → d , то мы можем записать c ∗→ d , что указывает на существование последовательности редукции от c до d . Формально,∗→является рефлексивно-транзитивным замыканием →. Используя пример из предыдущего абзаца, мы имеем (11+9)×(2+4) → 20×(2+4) и 20×(2+4) → 20×6, поэтому (11+9)×(2+4)∗→20×6.

После этого слияние можно определить следующим образом. a ∈ S считается сливающимся , если для всех пар b , c ∈ S таких, что a ∗→ б и а ∗→ c , существует d ∈ S с b ∗→ г и в ∗→ d (обозначается ). Если каждый a ∈ S является конфлюэнтным, мы говорим, что → является конфлюэнтным. Это свойство также иногда называют свойством алмаза , по форме диаграммы, показанной справа. Некоторые авторы резервируют термин свойство алмаза для варианта диаграммы с одиночными сокращениями везде; то есть, когда a → b и a → c , должно существовать d такое, что b → d и c → d . Вариант с одиночной редукцией строго сильнее, чем вариант с множественной редукцией. б ↓ с {\displaystyle b\mathbin {\downarrow } c}

Слияние грунта

Система переписывания терминов является базисно конфлюэнтной , если каждый базисный термин является конфлюэнтным, то есть каждый термин без переменных. [3]

Местное слияние

Рисунок 1: Циклическая, локально-конфлюэнтная, но не глобально-конфлюэнтная система перезаписи [4]
Рисунок 2: Бесконечная нециклическая, локально-конфлюэнтная, но не глобально-конфлюэнтная система перезаписи [4]

Элемент a ∈ S называется локально конфлюэнтным (или слабо конфлюэнтным [5] ), если для всех b , c ∈ S с a → b и a → c существует d ∈ S с b ∗→ г и в ∗→ d . Если каждый a ∈ S локально конфлюэнтен, то → называется локально конфлюэнтен или имеет слабое свойство Чёрча–Россера . Это отличается от конфлюэнтности тем, что b и c должны быть выведены из a за один шаг. По аналогии с этим, конфлюэнтность иногда называют глобальной конфлюэнтностью .

Отношение∗→, введенная как обозначение для последовательностей редукции, может рассматриваться как самостоятельная система переписывания, отношение которой является рефлексивно-транзитивным замыканием → . Поскольку последовательность последовательностей редукции снова является последовательностью редукции (или, что эквивалентно, поскольку формирование рефлексивно-транзитивного замыкания является идемпотентным ),∗∗→=∗→. Из этого следует, что → является конфлюэнтным тогда и только тогда, когда∗→локально сливается.

Система переписывания может быть локально конфлюэнтной, не будучи (глобально) конфлюэнтной. Примеры показаны на рисунках 1 и 2. Однако лемма Ньюмана утверждает, что если локально конфлюэнтная система переписывания не имеет бесконечных последовательностей редукции (в этом случае говорят, что она завершающая или сильно нормализующая ), то она глобально конфлюэнтна.

Собственность Черч-Россер

Говорят, что система переписывания обладает свойством Чёрча–Россера тогда и только тогда, когда подразумевает для всех объектов x , y . Алонзо Чёрч и Дж. Баркли Россер доказали в 1936 году, что лямбда-исчисление обладает этим свойством; [6] отсюда и название свойства. [7] (Тот факт, что лямбда-исчисление обладает этим свойством, также известен как теорема Чёрча–Россера .) В системе переписывания со свойством Чёрча–Россера проблема слов может быть сведена к поиску общего преемника. В системе Чёрча–Россера объект имеет не более одной нормальной формы ; то есть нормальная форма объекта уникальна, если она существует, но она может и не существовать. Например, в лямбда-исчислении выражение (λx.xx)(λx.xx) не имеет нормальной формы, поскольку существует бесконечная последовательность β-редукций (λx.xx)(λx.xx) → (λx.xx)(λx.xx) → ... [8] х ↔ ∗ у {\displaystyle x{\stackrel {*}{\leftrightarrow }}y} х ↓ у {\displaystyle x{\mathbin {\downarrow }}y}

Система переписывания обладает свойством Чёрча–Россера тогда и только тогда, когда она конфлюэнтна. [9] Из-за этой эквивалентности в литературе встречается довольно много вариаций в определениях. Например, в «Терезе» свойство Чёрча–Россера и конфлюэнтность определяются как синонимичные и идентичные определению конфлюэнтности, представленному здесь; Чёрч–Россер, как определено здесь, остаётся неназванным, но дано как эквивалентное свойство; это отклонение от других текстов является преднамеренным. [10]

Полуслияние

Определение локального слияния отличается от определения глобального слияния тем, что рассматриваются только элементы, достигнутые из данного элемента за один шаг переписывания. Рассматривая один элемент, достигнутый за один шаг, и другой элемент, достигнутый произвольной последовательностью, мы приходим к промежуточному понятию полуслияния: a ∈ S называется полуслиянием, если для всех b , c ∈ S с a → b и a ∗→ c существует d ∈ S с b ∗→ г и в ∗→ d ; если каждый a ∈ S является полуконфлюэнтным, мы говорим, что → является полуконфлюэнтным.

Полуконфлюентный элемент не обязательно должен быть конфлюентным, но полуконфлюентная система переписывания обязательно является конфлюентной, а конфлюентная система тривиально является полуконфлюентной.

Сильное слияние

Strong confluence — это еще одна вариация локального слияния, которая позволяет нам сделать вывод, что система переписывания является глобально конфлюэнтной. Элемент a ∈ S называется strong confluent , если для всех b , c ∈ S с a → b и a → c существует d ∈ S с b ∗→ d и либо c → d, либо c = d ; если каждый a ∈ S является строго конфлюэнтным, мы говорим, что → является строго конфлюэнтным.

Конфлюентный элемент не обязательно должен быть строго конфлюентным, но строго конфлюентная система переписывания обязательно является конфлюентной.

Примеры конфлюэнтных систем

Смотрите также

Примечания

  1. ^ затем вызвал правила перезаписи, чтобы подчеркнуть их ориентацию слева направо
  2. ^ Алгоритм завершения Кнута–Бендикса может быть использован для вычисления такой системы из заданного набора уравнений. Такая система, например, для групп, показана здесь , с ее предложениями, последовательно пронумерованными. Используя его, доказательство, например, R6, состоит в применении R11 и R12 в любом порядке к члену ( a −1 ) −1 ⋅1 для получения члена a ; никакие другие правила не применимы.

Ссылки

  1. ^ Уолтерс, Х. Р.; Зантема, Х. (октябрь 1994 г.). «Переписывание систем для целочисленной арифметики» (PDF) . Университет Утрехта.
  2. ^ Bläsius & Bürcckert 1992, стр. 134: названия аксиом и предложений следуют оригинальному тексту
  3. ^ Робинсон, Алан JA; Воронков, Андрей (5 июля 2001 г.). Справочник по автоматизированному рассуждению. Gulf Professional Publishing. стр. 560. ISBN 978-0-444-82949-8.
  4. ^ ab N. Dershowitz и J.-P. Jouannaud (1990). "Rewrite Systems". В Jan van Leeuwen (ред.). Formal Models and Semantics . Handbook of Theoretical Computer Science. Vol. B. Elsevier. pp. 243–320. ISBN 0-444-88074-7.Здесь: стр.268, рис.2а+б.
  5. ↑ Тереза ​​2003, стр. 10–11.
  6. ^ Алонзо Чёрч и Дж. Баркли Россер. Некоторые свойства обращения. Trans. AMS, 39:472-482, 1936
  7. ^ Баадер и Нипков 1998, стр. 9.
  8. ^ Купер, СБ (2004). Теория вычислимости . Бока-Ратон: Chapman & Hall/CRC. стр. 184. ISBN 1584882379.
  9. ^ Баадер и Нипков 1998, с. 11.
  10. ^ Тереза ​​2003, стр. 11.
  • «Тереза»; Безем, Марк; Клоп, Ян Виллем ; де Вриер, Роэль (2003). Системы переписывания терминов . Кембриджские трактаты по теоретической информатике. Издательство Кембриджского университета. ISBN 0-521-39115-6.
  • Баадер, Франц ; Нипков, Тобиас (1998). Переписывание терминов и все такое. Cambridge University Press. ISBN 978-0-521-77920-3.
  • Блазиус, К.Х.; Бюркерт, Х.-Ю., ред. (1992). Система вычетов . Ольденбург. п. 291.
Взято с "https://en.wikipedia.org/w/index.php?title=Confluence_(abstract_rewriting)&oldid=1241893152"