Алгоритм Чана

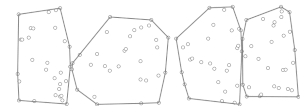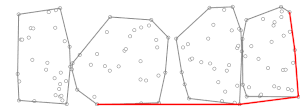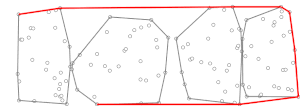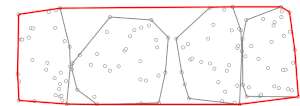
В вычислительной геометрии алгоритм Чана ^[1] , названный в честь Тимоти М. Чана , является оптимальным чувствительным к выходу алгоритмом для вычисления выпуклой оболочки набора точек в 2- или 3-мерном пространстве. Алгоритм занимает время, где — число вершин выходных данных (выпуклой оболочки). В плоском случае алгоритм объединяет алгоритм ( например, сканирование Грэма ) с маршем Джарвиса ( ), чтобы получить оптимальное время. Алгоритм Чана примечателен тем, что он намного проще алгоритма Киркпатрика–Зейделя , и он естественным образом распространяется на 3-мерное пространство. Эта парадигма ^[2] была независимо разработана Фрэнком Нильсеном в его докторской диссертации. ^[3]${\displaystyle P}$${\displaystyle n}$${\displaystyle O(n\log h)}$${\displaystyle ч}$${\displaystyle O(n\log n)}$${\displaystyle O(нч)}$${\displaystyle O(n\log h)}$

Для одного прохода алгоритма требуется параметр , который находится между 0 и (количеством точек нашего множества ). В идеале, однако , количество вершин в выходной выпуклой оболочке неизвестно в начале. Выполняется несколько проходов с увеличивающимися значениями , которые затем завершаются, когда (см. ниже о выборе параметра ).${\displaystyle м}$${\displaystyle n}$${\displaystyle P}$${\displaystyle м=ч}$${\displaystyle ч}$${\displaystyle м}$${\displaystyle m\geq h}$${\displaystyle м}$

Алгоритм начинается с произвольного разбиения набора точек на подмножества , каждое из которых содержит не более точек; обратите внимание, что .${\displaystyle P}$${\displaystyle K=\lceil n/m\rceil}$${\displaystyle (Q_{k})_{k=1,2,...K}}$${\displaystyle м}$${\displaystyle K=O(н/м)}$

Для каждого подмножества он вычисляет выпуклую оболочку, , используя алгоритм (например, сканирование Грэма ), где — количество точек в подмножестве. Поскольку существуют подмножества точек, эта фаза занимает время.${\displaystyle Q_{k}}$${\displaystyle C_{k}}$${\displaystyle O(p\log p)}$${\displaystyle p}$${\displaystyle К}$${\displaystyle O(м)}$${\displaystyle K\cdot O(m\log m)=O(n\log m)}$

Во время второй фазы выполняется марш Джарвиса с использованием предварительно вычисленных (мини) выпуклых оболочек, . На каждом шаге этого алгоритма марша Джарвиса у нас есть точка в выпуклой оболочке (в начале это может быть точка в с наименьшей координатой y, которая гарантированно находится в выпуклой оболочке ), и нужно найти точку такую, чтобы все остальные точки находились справа от линии ^{[ необходимо разъяснение ]} , где обозначение просто означает, что следующая точка, то есть , определяется как функция и . Выпуклая оболочка множества , , известна и содержит не более точек (перечисленных по часовой стрелке или против часовой стрелки), что позволяет производить вычисления за время с помощью бинарного поиска ^{[ как? ]} . Следовательно, вычисление для всех подмножеств может быть выполнено за время. Затем мы можем определить, используя ту же технику, которая обычно используется в марше Джарвиса, но рассматривая только точки (т. е. точки в мини-выпуклых оболочках) вместо всего множества . Для этих точек одна итерация марша Джарвиса равна , что пренебрежимо мало по сравнению с вычислением для всех подмножеств. Марш Джарвиса завершается, когда процесс повторяется несколько раз (потому что, согласно принципу работы марша Джарвиса, после не более чем итераций его самого внешнего цикла, где — количество точек в выпуклой оболочке , мы должны были найти выпуклую оболочку), следовательно, вторая фаза занимает время, эквивалентное времени , если близко к (см. ниже описание стратегии выбора, чтобы это было так).${\displaystyle (C_{k})_{k=1,2,...K}}$${\displaystyle p_{i}}$${\displaystyle p_{i}}$${\displaystyle P}$${\displaystyle P}$${\displaystyle p_{i+1}=f(p_{i},P)}$${\displaystyle P}$${\displaystyle p_{i}p_{i+1}}$${\displaystyle p_{i+1}=f(p_{i},P)}$${\displaystyle p_{i+1}}$${\displaystyle p_{i}}$${\displaystyle P}$${\displaystyle Q_{k}}$${\displaystyle C_{k}}$${\displaystyle м}$${\displaystyle f(p_{i},Q_{k})}$${\displaystyle O(\log m)}$${\displaystyle f(p_{i},Q_{k})}$${\displaystyle К}$${\displaystyle O(K\log m)}$${\displaystyle f(p_{i},P)}$${\displaystyle (f(p_{i},Q_{k}))_{1\leq k\leq K}}$${\displaystyle P}$${\displaystyle O(К)}$${\displaystyle O(h)}$${\displaystyle ч}$${\displaystyle ч}$${\displaystyle P}$${\displaystyle O(Kh\log m)}$${\displaystyle O(n\log h)}$${\displaystyle м}$${\displaystyle ч}$${\displaystyle м}$

Выполняя две описанные выше фазы, во времени вычисляется выпуклая оболочка точек .${\displaystyle n}$${\displaystyle O(n\log h)}$

Если для выбрано произвольное значение , может случиться, что . В этом случае после шагов во второй фазе мы прерываем марш Джарвиса , так как его прогон до конца занял бы слишком много времени. В этот момент время будет потрачено, а выпуклая оболочка не будет рассчитана.${\displaystyle м}$${\displaystyle м<ч}$${\displaystyle м}$${\displaystyle O(n\log m)}$

Идея состоит в том, чтобы сделать несколько проходов алгоритма с увеличивающимися значениями ; каждый проход завершается (успешно или неудачно) со временем. Если увеличивается слишком медленно между проходами, число итераций может быть большим; с другой стороны, если оно увеличивается слишком быстро, первое, для которого алгоритм завершается успешно, может быть намного больше , и производить сложность .${\displaystyle м}$${\displaystyle O(n\log m)}$${\displaystyle м}$${\displaystyle м}$${\displaystyle ч}$${\displaystyle O(n\log m)>O(n\log h)}$

Одна из возможных стратегий — возводить в квадрат значение на каждой итерации, вплоть до максимального значения (соответствующего разбиению на одноэлементные множества). ^[4] Начиная со значения 2, на итерации выбирается . В этом случае итерации выполняются, учитывая, что алгоритм завершается, как только мы имеем${\displaystyle м}$${\displaystyle n}$${\displaystyle т}$${\displaystyle m=\min \left(n,2^{2^{t}}\right)}$${\displaystyle O(\log \log h)}$

${\displaystyle m=2^{2^{t}}\geq h\если и только если \log \left(2^{2^{t}}\right)\geq \log h\если и только если 2^{t}\geq \log h\если и только если \log {2^{t}}\geq \log {\log h}\если и только если t\geq \log {\log h},}$

с логарифмом, взятым по основанию , а общее время работы алгоритма равно${\displaystyle 2}$

${\displaystyle \sum _{t=0}^{\lceil \log \log h\rceil }O\left(n\log \left(2^{2^{t}}\right)\right)=O(n)\sum _{t=0}^{\lceil \log \log h\rceil }2^{t}=O\left(n\cdot 2^{1+\lceil \log \log h\rceil }\right)=O(n\log h).}$

Для обобщения этой конструкции для 3-мерного случая вместо сканирования Грэма следует использовать алгоритм вычисления 3-мерной выпуклой оболочки Препараты и Хонга, а также 3-мерную версию марша Джарвиса. Временная сложность остается . ^[1]${\displaystyle O(n\log n)}$${\displaystyle O(n\log h)}$

В следующем псевдокоде текст в скобках и курсивом является комментариями. Для полного понимания следующего псевдокода рекомендуется, чтобы читатель уже был знаком с алгоритмами сканирования Грэма и марша Джарвиса для вычисления выпуклой оболочки, , набора точек, .${\displaystyle С}$${\displaystyle P}$

Вход: Задайте с помощью точек.${\displaystyle P}$${\displaystyle n}$

Выходные данные: множество точек , выпуклая оболочка .${\displaystyle С}$${\displaystyle ч}$${\displaystyle P}$

(Выберите точку, которая гарантированно находится в : например, точку с наименьшей координатой y.)${\displaystyle P}$${\displaystyle С}$

(Эта операция требует времени: например, мы можем просто выполнить итерацию .)${\displaystyle {\mathcal {O}}(n)}$${\displaystyle P}$

${\displaystyle p_{1}:=ВЫБРАТЬ\_START(P)}$

( используется в части марша Джарвиса этого алгоритма Чана,${\displaystyle p_{0}}$

так что для вычисления второй точки, , в выпуклой оболочке .)${\displaystyle p_{2}}$${\displaystyle P}$

(Примечание: это не точка .)${\displaystyle p_{0}}$${\displaystyle P}$

(Более подробную информацию см. в комментариях рядом с соответствующей частью алгоритма Чана.)

${\displaystyle p_{0}:=(-\infty,0)}$

(Примечание: количество точек в конечной выпуклой оболочке неизвестно . )${\displaystyle ч}$${\displaystyle P}$

(Это итерации, необходимые для нахождения значения , которое является оценкой .)${\displaystyle м}$${\displaystyle ч}$

( требуется для этого алгоритма Чана для нахождения выпуклой оболочки .)${\displaystyle h\leq m}$${\displaystyle P}$

(Более конкретно, мы хотим , чтобы не выполнять слишком много ненужных итераций${\displaystyle h\leq m\leq h^{2}}$

и поэтому временная сложность этого алгоритма Чана равна .)${\displaystyle {\mathcal {O}}(n\log h)}$

(Как объяснялось выше в этой статье, используется стратегия, при которой для нахождения требуется максимум итераций .)${\displaystyle \log \log n}$${\displaystyle м}$

(Примечание: финал может быть не равен , но он никогда не будет меньше и больше .)${\displaystyle м}$${\displaystyle ч}$${\displaystyle ч}$${\displaystyle h^{2}}$

(Тем не менее, этот алгоритм Чана останавливается после выполнения итераций самого внешнего цикла,${\displaystyle ч}$

то есть, даже если , он не выполняет итерации самого внешнего цикла.)${\displaystyle m\neq h}$${\displaystyle м}$

(Более подробную информацию см. ниже в части марша Джарвиса этого алгоритма, где возвращается значение , если .)${\displaystyle С}$${\displaystyle p_{i+1}==p_{1}}$

для делать${\displaystyle 1\leq t\leq \log \log n}$

(Установите параметр для текущей итерации. Используется «схема возведения в квадрат», описанная выше в этой статье.${\displaystyle м}$

Существуют и другие схемы: например, «схема удвоения», где , для .${\displaystyle m=2^{t}}$${\displaystyle t=1,\dots ,\left\lceil \log h\right\rceil }$

Однако если использовать «схему удвоения», то результирующая временная сложность этого алгоритма Чана составит .)${\displaystyle {\mathcal {O}}(n\log ^{2}h)}$

${\displaystyle м:=2^{2^{т}}}$

(Инициализируйте пустой список (или массив) для хранения точек выпуклой оболочки по мере их нахождения.)${\displaystyle P}$

${\displaystyle C:=()}$

${\displaystyle ДОБАВИТЬ(C,p_{1})}$

(Произвольно разбить множество точек на подмножества, каждое из которых содержит примерно по 10 элементов.)${\displaystyle P}$${\displaystyle K=\left\lceil {\frac {n}{m}}\right\rceil }$${\displaystyle м}$

${\displaystyle Q_{1},Q_{2},\dots ,Q_{K}:=РАЗДЕЛИТЬ(P,m)}$

(Вычислить выпуклую оболочку всех подмножеств точек, .)${\displaystyle К}$${\displaystyle Q_{1},Q_{2},\точки ,Q_{K}}$

(Это требует времени.)${\displaystyle {\mathcal {O}}(Km\log m) = {\mathcal {O}}(n\log m)}$

Если , то временная сложность равна .)${\displaystyle m\leq h^{2}}$${\displaystyle {\mathcal {O}}(n\log h^{2}) = {\mathcal {O}}(n\log h)}$

для делать${\displaystyle 1\leq k\leq K}$

(Вычислить выпуклую оболочку подмножества , , используя сканирование Грэма, что требует времени.)${\displaystyle к}$${\displaystyle Q_{k}}$${\displaystyle {\mathcal {O}}(м\log м)}$

( — выпуклая оболочка подмножества точек .)${\displaystyle C_{k}}$${\displaystyle Q_{k}}$

${\displaystyle C_{k}:=GRAHAM\_SCAN(Q_{k})}$

(На этом этапе были вычислены выпуклые оболочки соответствующих подмножеств точек .)${\displaystyle C_{1},C_{2},\dots ,C_{K}}$${\displaystyle Q_{1},Q_{2},\dots ,Q_{K}}$

(Теперь воспользуемся модифицированной версией алгоритма марша Джарвиса для вычисления выпуклой оболочки .)${\displaystyle P}$

(Марш Джарвиса выполняется за время, где — количество входных точек, а — количество точек в выпуклой оболочке.)${\displaystyle {\mathcal {O}}(nh)}$${\displaystyle n}$${\displaystyle h}$

(Учитывая, что алгоритм Jarvis March чувствителен к выходным данным , время его работы зависит от размера выпуклой оболочки. )${\displaystyle h}$

(На практике это означает, что марш Джарвиса выполняет итерации своего самого внешнего цикла.${\displaystyle h}$

На каждой из этих итераций выполняется не более одного раза в течение самого внутреннего цикла.)${\displaystyle n}$

(Мы хотим , поэтому мы не хотим выполнять больше итераций в следующем внешнем цикле.)${\displaystyle h\leq m\leq h^{2}}$${\displaystyle m}$

(Если ток меньше , т.е. , выпуклая оболочка не может быть найдена.)${\displaystyle m}$${\displaystyle h}$${\displaystyle m<h}$${\displaystyle P}$

(В этой модифицированной версии марша Джарвиса мы выполняем операцию внутри самого внутреннего цикла, которая требует времени.${\displaystyle {\mathcal {O}}(\log m)}$

Таким образом, общая временная сложность этой модифицированной версии составляет

${\displaystyle {\mathcal {O}}(mK\log m)={\mathcal {O}}(m\left\lceil {\frac {n}{m}}\right\rceil \log m)={\mathcal {O}}(n\log m)={\mathcal {O}}(n\log 2^{2^{t}})={\mathcal {O}}(n2^{t}).}$

Если , то временная сложность равна .)${\displaystyle m\leq h^{2}}$${\displaystyle {\mathcal {O}}(n\log h^{2})={\mathcal {O}}(n\log h)}$

для делать${\displaystyle 1\leq i\leq m}$

(Примечание: здесь точка в выпуклой оболочке уже известна, то есть .)${\displaystyle P}$${\displaystyle p_{1}}$

(В этом внутреннем цикле for вычисляются возможные следующие точки, которые будут находиться на выпуклой оболочке , , .)${\displaystyle K}$${\displaystyle P}$${\displaystyle q_{i,1},q_{i,2},\dots ,q_{i,K}}$

(Каждый из этих возможных следующих пунктов взят из разных источников :${\displaystyle K}$${\displaystyle C_{k}}$

то есть является возможной следующей точкой на выпуклой оболочке , которая является частью выпуклой оболочки .)${\displaystyle q_{i,k}}$${\displaystyle P}$${\displaystyle C_{k}}$

(Примечание: зависит от : то есть для каждой итерации существуют возможные следующие точки, которые могут находиться на выпуклой оболочке .)${\displaystyle q_{i,1},q_{i,2},\dots ,q_{i,K}}$${\displaystyle i}$${\displaystyle i}$${\displaystyle K}$${\displaystyle P}$

(Примечание: на каждой итерации только одна из точек среди добавляется к выпуклой оболочке .)${\displaystyle i}$${\displaystyle q_{i,1},q_{i,2},\dots ,q_{i,K}}$${\displaystyle P}$

для делать${\displaystyle 1\leq k\leq K}$

( находит точку , в которой угол максимален ^{[ почему? ]} ,${\displaystyle JARVIS\_BINARY\_SEARCH}$${\displaystyle d\in C_{k}}$${\displaystyle \measuredangle p_{i-1}p_{i}d}$

где - угол между векторами и . Такой хранится в .)${\displaystyle \measuredangle p_{i-1}p_{i}d}$${\displaystyle {\overrightarrow {p_{i}p_{i-1}}}}$${\displaystyle {\overrightarrow {p_{i}d}}}$${\displaystyle d}$${\displaystyle q_{i,k}}$

(Углы не обязательно рассчитывать напрямую: можно использовать тест на ориентацию ^{[ как? ]} .)

( можно выполнить вовремя ^{[ как? ]} .)${\displaystyle JARVIS\_BINARY\_SEARCH}$${\displaystyle {\mathcal {O}}(\log m)}$

(Примечание : на итерации известно и является точкой в ​​выпуклой оболочке :${\displaystyle i=1}$${\displaystyle p_{i-1}=p_{0}=(-\infty ,0)}$${\displaystyle p_{1}}$${\displaystyle P}$

в данном случае это точка с наименьшей координатой y.)${\displaystyle P}$

${\displaystyle q_{i,k}:=JARVIS\_BINARY\_SEARCH(p_{i-1},p_{i},C_{k})}$

(Выберите точку , которая максимизирует угол ^{[ почему? ]} , чтобы она стала следующей точкой на выпуклой оболочке .)${\displaystyle z\in \{q_{i,1},q_{i,2},\dots ,q_{i,K}\}}$${\displaystyle \measuredangle p_{i-1}p_{i}z}$ ${\displaystyle P}$

${\displaystyle p_{i+1}:=JARVIS\_NEXT\_CH\_POINT(p_{i-1},p_{i},(q_{i,1},q_{i,2},\dots ,q_{i,K}))}$

(Марш Джарвиса заканчивается, когда следующая выбранная точка на выпуклой оболочке, , становится начальной точкой, .)${\displaystyle p_{i+1}}$${\displaystyle p_{1}}$

если ${\displaystyle p_{i+1}==p_{1}}$

(Вернуть выпуклую оболочку , содержащую точки.)${\displaystyle P}$${\displaystyle i=h}$

(Примечание: конечно, нет необходимости возвращать , что равно .)${\displaystyle p_{i+1}}$${\displaystyle p_{1}}$

возвращаться ${\displaystyle C:=(p_{1},p_{2},\dots ,p_{i})}$

еще

${\displaystyle ADD(C,p_{i+1})}$

(Если после итераций не найдена точка такая, что , то .)${\displaystyle m}$${\displaystyle p_{i+1}}$${\displaystyle p_{i+1}==p_{1}}$${\displaystyle m<h}$

(Нам нужно начать заново с более высоким значением .)${\displaystyle m}$

В статье Чана содержится несколько предложений, которые могут улучшить практическую эффективность алгоритма, например:

• При вычислении выпуклых оболочек подмножеств исключите из рассмотрения в последующих вычислениях точки, не входящие в выпуклую оболочку.
• Выпуклые оболочки более крупных наборов точек можно получить путем слияния ранее вычисленных выпуклых оболочек, а не пересчета с нуля.
• С вышеизложенной идеей, доминирующая стоимость алгоритма заключается в предварительной обработке, т. е. вычислении выпуклых оболочек групп. Чтобы уменьшить эту стоимость, мы можем рассмотреть повторное использование оболочек, вычисленных из предыдущей итерации, и их слияние по мере увеличения размера группы.

В статье Чана описываются и другие проблемы, известные алгоритмы которых можно сделать максимально чувствительными к выходным данным, используя его методику, например:

• Вычисление нижней огибающей набора отрезков прямой, которая определяется как нижняя граница неограниченной трапеции , образованной пересечениями.${\displaystyle L(S)}$${\displaystyle S}$${\displaystyle n}$
• Хершбергер ^[5] дал алгоритм, который можно ускорить до , где h — число ребер в конверте${\displaystyle O(n\log n)}$${\displaystyle O(n\log h)}$

• Построение выходных чувствительных алгоритмов для многомерных выпуклых оболочек. С использованием группирующих точек и эффективных структур данных сложность может быть достигнута при условии, что h имеет полиномиальный порядок в .${\displaystyle O(n\log h)}$${\displaystyle n}$

• Алгоритмы выпуклой оболочки