Двоичный поиск
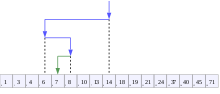 Визуализация алгоритма бинарного поиска, где 7 — целевое значение | |
| Сорт | Алгоритм поиска |
|---|---|
| Структура данных | Множество |
| Худший вариант производительности | О (лог n ) |
| Лучшая производительность | О (1) |
| Средняя производительность | О (лог n ) |
| Наихудшая сложность пространства | О (1) |
| Оптимальный | Да |
В информатике бинарный поиск , также известный как поиск по полуинтервалу , [1] логарифмический поиск , [2] или двоичный отрыв , [3] — это алгоритм поиска , который находит положение целевого значения в отсортированном массиве . [4] [5] Двоичный поиск сравнивает целевое значение со средним элементом массива. Если они не равны, половина, в которой не может находиться цель, исключается, и поиск продолжается на оставшейся половине, снова беря средний элемент для сравнения с целевым значением и повторяя это до тех пор, пока целевое значение не будет найдено. Если поиск заканчивается, а оставшаяся половина оказывается пустой, цели нет в массиве.
Двоичный поиск выполняется за логарифмическое время в худшем случае , выполняя сравнения, где — количество элементов в массиве. [a] [6] Двоичный поиск быстрее линейного поиска , за исключением небольших массивов. Однако массив должен быть сначала отсортирован, чтобы можно было применить бинарный поиск. Существуют специализированные структуры данных , предназначенные для быстрого поиска, такие как хэш-таблицы , поиск по которым можно выполнять эффективнее, чем бинарный поиск. Однако бинарный поиск можно использовать для решения более широкого круга задач, таких как поиск следующего наименьшего или следующего наибольшего элемента в массиве относительно целевого, даже если он отсутствует в массиве.
Существует множество вариаций бинарного поиска. В частности, дробное каскадирование ускоряет бинарный поиск одного и того же значения в нескольких массивах. Дробное каскадирование эффективно решает ряд задач поиска в вычислительной геометрии и во многих других областях. Экспоненциальный поиск расширяет бинарный поиск до неограниченных списков. Структуры данных двоичного дерева поиска и B-дерева основаны на двоичном поиске.
Алгоритм
Двоичный поиск работает на отсортированных массивах. Двоичный поиск начинается со сравнения элемента в середине массива с целевым значением. Если целевое значение совпадает с элементом, возвращается его позиция в массиве. Если целевое значение меньше элемента, поиск продолжается в нижней половине массива. Если целевое значение больше элемента, поиск продолжается в верхней половине массива. Делая это, алгоритм исключает половину, в которой целевое значение не может находиться в каждой итерации. [7]
Процедура
При наличии массива элементов со значениями или записями, отсортированными таким образом, что , и целевого значения , следующая подпрограмма использует двоичный поиск для нахождения индекса в . [7]
- Установите на и на .
- Если , то поиск завершается как безуспешный.
- Установите (положение среднего элемента) равным полу числа , которое является наибольшим целым числом, меньшим или равным .
- Если , установите и перейдите к шагу 2.
- Если , установите и перейдите к шагу 2.
- Теперь поиск завершен; возвращаемся .
Эта итеративная процедура отслеживает границы поиска с двумя переменными и . Процедуру можно выразить в псевдокоде следующим образом, где имена и типы переменных остаются такими же, как и выше, является функцией пола и ссылается на конкретное значение, которое передает неудачу поиска. [7]floorunsuccessful

Функция binary_search(A, n, T) — это Л := 0 Р := n − 1 пока L ≤ R делать м := пол((Д + П) / 2) если А[м] < Т тогда Л := м + 1 иначе если A[m] > T тогда Р := м − 1 в противном случае : возврат m возврат неудачный
В качестве альтернативы алгоритм может взять потолок . Это может изменить результат, если целевое значение встречается в массиве более одного раза.
Альтернативная процедура
В вышеприведенной процедуре алгоритм проверяет, равен ли средний элемент ( ) целевому элементу ( ) в каждой итерации. Некоторые реализации опускают эту проверку во время каждой итерации. Алгоритм будет выполнять эту проверку только тогда, когда остается один элемент (когда ). Это приводит к более быстрому циклу сравнения, поскольку одно сравнение исключается за итерацию, в то время как в среднем требуется только одна дополнительная итерация. [8]
Первую реализацию, исключающую эту проверку, Герман Боттенбрух опубликовал в 1962 году. [8] [9]
- Установите на и на .
- Пока ,
- Установите (положение среднего элемента) на потолок , который является наименьшим целым числом, большим или равным .
- Если , установите .
- В противном случае, ; установить в .
- Теперь поиск выполнен. Если , вернуть . В противном случае поиск завершается как неудачный.
Где ceilнаходится функция потолка, псевдокод для этой версии:
Функция binary_search_alternative(A, n, T) — это Л := 0 Р := n − 1 пока L != R делать м := ceil((L + R) / 2) если А[м] > Т тогда Р := м − 1 еще : Д := м если A[L] = T , то вернуть L вернуть неудачу
Дублирующие элементы
Процедура может возвращать любой индекс, элемент которого равен целевому значению, даже если в массиве есть дубликаты элементов. Например, если массив для поиска был , а цель была , то было бы правильным для алгоритма вернуть либо 4-й (индекс 3), либо 5-й (индекс 4) элемент. Обычная процедура вернула бы 4-й элемент (индекс 3) в этом случае. Она не всегда возвращает первый дубликат (подумайте, какой из них все еще возвращает 4-й элемент). Однако иногда необходимо найти самый левый элемент или самый правый элемент для целевого значения, которое дублируется в массиве. В приведенном выше примере 4-й элемент является самым левым элементом значения 4, в то время как 5-й элемент является самым правым элементом значения 4. Альтернативная процедура выше всегда будет возвращать индекс самого правого элемента, если такой элемент существует. [9]
Процедура нахождения самого левого элемента
Чтобы найти самый левый элемент, можно использовать следующую процедуру: [10]
- Установите на и на .
- Пока ,
- Установите (положение среднего элемента) равным полу числа , которое является наибольшим целым числом, меньшим или равным .
- Если , установите .
- В противном случае, ; установить в .
- Возвращаться .
Если и , то — самый левый элемент, равный . Даже если нет в массиве, — это ранг в массиве или количество элементов в массиве, которые меньше .
Где floorнаходится функция пола, псевдокод для этой версии:
функция binary_search_leftmost(A, n, T): Л := 0 Р := н в то время как L < R: м := пол((Д + П) / 2) если А[м] < Т: Л := м + 1 еще : Р := м возврат Л
Процедура нахождения самого правого элемента
Чтобы найти самый правый элемент, можно использовать следующую процедуру: [10]
- Установите на и на .
- Пока ,
- Установите (положение среднего элемента) равным полу числа , которое является наибольшим целым числом, меньшим или равным .
- Если , установите .
- В противном случае, ; установить в .
- Возвращаться .
Если и , то — самый правый элемент, который равен . Даже если нет в массиве, — это количество элементов в массиве, которые больше .
Где floorнаходится функция пола, псевдокод для этой версии:
функция binary_search_rightmost(A, n, T): Л := 0 Р := н в то время как L < R: м := пол((Д + П) / 2) если А[м] > Т: Р := м еще : Л := м + 1 возврат Р - 1
Приблизительные совпадения

Вышеуказанная процедура выполняет только точные совпадения, находя позицию целевого значения. Однако расширение бинарного поиска для выполнения приблизительных совпадений является тривиальным, поскольку бинарный поиск работает с отсортированными массивами. Например, бинарный поиск может быть использован для вычисления для заданного значения его ранга (количества меньших элементов), предшественника (следующего наименьшего элемента), последователя (следующего наибольшего элемента) и ближайшего соседа . Запросы диапазона, ищущие количество элементов между двумя значениями, могут быть выполнены с двумя ранговыми запросами. [11]
- Запросы ранга могут быть выполнены с помощью процедуры поиска самого левого элемента. Количество элементов, меньших целевого значения, возвращается процедурой. [11]
- Запросы предшественников могут быть выполнены с помощью запросов ранга. Если ранг целевого значения равен , его предшественник равен . [12]
- Для запросов на преемника можно использовать процедуру поиска самого правого элемента. Если результатом выполнения процедуры для целевого значения является , то преемником целевого значения является . [12]
- Ближайшим соседом целевого значения является либо его предшественник, либо его последующий элемент, в зависимости от того, что ближе.
- Запросы диапазона также просты. [12] После того, как ранги двух значений известны, количество элементов, больших или равных первому значению и меньших второго, является разностью двух рангов. Это количество может быть скорректировано вверх или вниз на единицу в зависимости от того, следует ли считать конечные точки диапазона частью диапазона и содержит ли массив записи, соответствующие этим конечным точкам. [13]
Производительность

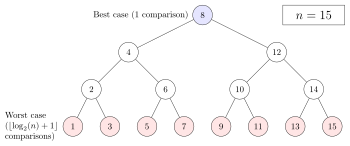
С точки зрения количества сравнений производительность бинарного поиска можно проанализировать, просмотрев выполнение процедуры на бинарном дереве. Корневой узел дерева является средним элементом массива. Средний элемент нижней половины является левым дочерним узлом корня, а средний элемент верхней половины является правым дочерним узлом корня. Остальная часть дерева строится аналогичным образом. Начиная с корневого узла, левые или правые поддеревья обходят в зависимости от того, меньше или больше целевое значение рассматриваемого узла. [6] [14]
В худшем случае бинарный поиск выполняет итерации цикла сравнения, где обозначение обозначает функцию пола , которая выдает наибольшее целое число, меньшее или равное аргументу, и является двоичным логарифмом . Это происходит потому, что наихудший случай достигается, когда поиск достигает самого глубокого уровня дерева, а в дереве всегда есть уровни для любого бинарного поиска.
Худший случай также может быть достигнут, когда целевой элемент отсутствует в массиве. Если на единицу меньше степени двойки, то это всегда так. В противном случае поиск может выполнять итерации, если поиск достигает самого глубокого уровня дерева. Однако он может выполнять итерации, что на единицу меньше худшего случая, если поиск заканчивается на втором самом глубоком уровне дерева. [15]
В среднем, предполагая, что каждый элемент с одинаковой вероятностью будет найден, бинарный поиск делает итерации, когда целевой элемент находится в массиве. Это приблизительно равно итерациям. Когда целевой элемент отсутствует в массиве, бинарный поиск делает итерации в среднем, предполагая, что диапазон между и за пределами элементов с одинаковой вероятностью будет найден. [14]
В лучшем случае, когда целевое значение является средним элементом массива, его позиция возвращается после одной итерации. [16]
С точки зрения итераций, ни один алгоритм поиска, который работает только путем сравнения элементов, не может показать лучшую среднюю и худшую производительность, чем бинарный поиск. Дерево сравнения, представляющее бинарный поиск, имеет наименьшее возможное количество уровней, поскольку каждый уровень выше самого нижнего уровня дерева заполнен полностью. [b] В противном случае алгоритм поиска может исключить несколько элементов за итерацию, увеличив количество итераций, требуемых в среднем и худшем случае. Это касается других алгоритмов поиска, основанных на сравнениях, поскольку, хотя они могут работать быстрее на некоторых целевых значениях, средняя производительность по всем элементам хуже, чем у бинарного поиска. Разделив массив пополам, бинарный поиск гарантирует, что размер обоих подмассивов будет максимально схожим. [14]
Сложность пространства
Двоичный поиск требует три указателя на элементы, которые могут быть индексами массива или указателями на ячейки памяти, независимо от размера массива. Таким образом, пространственная сложность бинарного поиска заключается в модели вычислений Word RAM .
Вывод среднего случая
Среднее число итераций, выполняемых бинарным поиском, зависит от вероятности поиска каждого элемента. Средний случай отличается для успешных и неудачных поисков. Предполагается, что каждый элемент с одинаковой вероятностью будет найден для успешного поиска. Для неудачных поисков предполагается, что интервалы между элементами и за их пределами с одинаковой вероятностью будут найдены. Средний случай для успешных поисков — это количество итераций, необходимых для поиска каждого элемента ровно один раз, деленное на , количество элементов. Средний случай для неудачных поисков — это количество итераций, необходимых для поиска элемента внутри каждого интервала ровно один раз, деленное на интервалы. [14]
Успешные поиски
В представлении двоичного дерева успешный поиск может быть представлен путем от корня до целевого узла, называемым внутренним путем . Длина пути — это количество ребер (соединений между узлами), через которые проходит путь. Количество итераций, выполненных поиском, при условии, что соответствующий путь имеет длину , подсчитывает начальную итерацию. Длина внутреннего пути — это сумма длин всех уникальных внутренних путей. Поскольку существует только один путь от корня до любого отдельного узла, каждый внутренний путь представляет собой поиск определенного элемента. Если есть элементы , что является положительным целым числом, а длина внутреннего пути равна , то среднее количество итераций для успешного поиска , с одной итерацией, добавленной для подсчета начальной итерации. [14]
Поскольку бинарный поиск является оптимальным алгоритмом поиска со сравнениями, эта задача сводится к вычислению минимальной длины внутреннего пути всех бинарных деревьев с узлами, которая равна: [17]
Например, в массиве из 7 элементов корень требует одной итерации, два элемента ниже корня требуют двух итераций, а четыре элемента ниже требуют трех итераций. В этом случае внутренняя длина пути равна: [17]
Среднее число итераций будет основано на уравнении для среднего случая. Сумма для может быть упрощена до: [14]
Подставим уравнение для в уравнение для : [14]
Для целого числа это эквивалентно уравнению для среднего случая успешного поиска, указанному выше.
Безуспешные поиски
Неудачные поиски могут быть представлены путем дополнения дерева внешними узлами , что образует расширенное двоичное дерево . Если внутренний узел или узел, присутствующий в дереве, имеет менее двух дочерних узлов, то добавляются дополнительные дочерние узлы, называемые внешними узлами, так что каждый внутренний узел имеет двух дочерних узлов. Таким образом, неудачный поиск может быть представлен как путь к внешнему узлу, родительским элементом которого является единственный элемент, который остается во время последней итерации. Внешний путь — это путь от корня к внешнему узлу. Длина внешнего пути — это сумма длин всех уникальных внешних путей. Если есть элементы , что является положительным целым числом, и длина внешнего пути равна , то среднее число итераций для неудачного поиска , с одной итерацией, добавленной для подсчета начальной итерации. Длина внешнего пути делится на вместо , потому что есть внешние пути, представляющие интервалы между элементами массива и за его пределами. [14]
Эту задачу можно аналогично свести к определению минимальной длины внешнего пути всех бинарных деревьев с узлами. Для всех бинарных деревьев длина внешнего пути равна длине внутреннего пути плюс . [17] Подставляя уравнение для : [14]
Подставляя уравнение для в уравнение для , можно определить средний случай безуспешных поисков: [14]
Выполнение альтернативной процедуры
Каждая итерация процедуры бинарного поиска, определенной выше, выполняет одно или два сравнения, проверяя, равен ли средний элемент целевому элементу в каждой итерации. Предполагая, что каждый элемент с равной вероятностью будет найден, каждая итерация выполняет в среднем 1,5 сравнения. Разновидность алгоритма проверяет, равен ли средний элемент целевому элементу в конце поиска. В среднем это исключает половину сравнения из каждой итерации. Это немного сокращает время, затрачиваемое на итерацию на большинстве компьютеров. Однако это гарантирует, что поиск займет максимальное количество итераций, в среднем добавляя одну итерацию к поиску. Поскольку цикл сравнения выполняется только один раз в худшем случае, небольшое увеличение эффективности на итерацию не компенсирует дополнительную итерацию для всех, кроме очень больших . [c] [18] [19]
Время работы и использование кэша
При анализе производительности бинарного поиска еще одним соображением является время, необходимое для сравнения двух элементов. Для целых чисел и строк необходимое время увеличивается линейно с увеличением длины кодирования (обычно количества бит ) элементов. Например, сравнение пары 64-битных беззнаковых целых чисел потребует сравнения до двух бит, чем сравнение пары 32-битных беззнаковых целых чисел. Наихудший случай достигается, когда целые числа равны. Это может быть существенным, когда длина кодирования элементов велика, например, в случае больших целочисленных типов или длинных строк, что делает сравнение элементов дорогим. Кроме того, сравнение значений с плавающей точкой (наиболее распространенное цифровое представление действительных чисел ) часто обходится дороже, чем сравнение целых чисел или коротких строк.
В большинстве компьютерных архитектур процессор имеет аппаратный кэш, отдельный от ОЗУ . Поскольку они расположены внутри самого процессора, доступ к кэшам осуществляется намного быстрее, но обычно они хранят гораздо меньше данных, чем ОЗУ. Поэтому большинство процессоров хранят ячейки памяти, к которым недавно был выполнен доступ, вместе с ячейками памяти, близкими к ним. Например, при доступе к элементу массива сам элемент может быть сохранен вместе с элементами, которые хранятся близко к нему в ОЗУ, что ускоряет последовательный доступ к элементам массива, которые близки по индексу друг к другу ( локальность ссылки ). В отсортированном массиве двоичный поиск может переходить к удаленным ячейкам памяти, если массив большой, в отличие от алгоритмов (таких как линейный поиск и линейное зондирование в хэш-таблицах ), которые обращаются к элементам последовательно. Это немного увеличивает время выполнения двоичного поиска для больших массивов в большинстве систем. [20]
Двоичный поиск по сравнению с другими схемами
Сортированные массивы с бинарным поиском являются очень неэффективным решением, когда операции вставки и удаления чередуются с извлечением, что занимает время для каждой такой операции. Кроме того, отсортированные массивы могут усложнить использование памяти, особенно когда элементы часто вставляются в массив. [21] Существуют другие структуры данных, которые поддерживают гораздо более эффективную вставку и удаление. Двоичный поиск может использоваться для выполнения точного сопоставления и установки членства (определения того, находится ли целевое значение в коллекции значений). Существуют структуры данных, которые поддерживают более быстрое точное сопоставление и установку членства. Однако, в отличие от многих других схем поиска, бинарный поиск может использоваться для эффективного приблизительного сопоставления, обычно выполняя такие сопоставления во времени независимо от типа или структуры самих значений. [22] Кроме того, существуют некоторые операции, такие как поиск наименьшего и наибольшего элемента, которые могут быть эффективно выполнены на отсортированном массиве. [11]
Линейный поиск
Линейный поиск — это простой алгоритм поиска, который проверяет каждую запись, пока не найдет целевое значение. Линейный поиск можно выполнять в связанном списке, что позволяет выполнять вставку и удаление быстрее, чем массив. Двоичный поиск быстрее линейного поиска для отсортированных массивов, за исключением случаев, когда массив короткий, хотя массив необходимо предварительно отсортировать. [d] [24] Все алгоритмы сортировки, основанные на сравнении элементов, такие как быстрая сортировка и сортировка слиянием , требуют как минимум сравнений в худшем случае. [25] В отличие от линейного поиска, бинарный поиск можно использовать для эффективного приблизительного сопоставления. Существуют такие операции, как поиск наименьшего и наибольшего элемента, которые можно эффективно выполнить для отсортированного массива, но не для несортированного. [26]
Деревья

Двоичное дерево поиска — это структура данных бинарного дерева , которая работает на основе принципа бинарного поиска. Записи дерева располагаются в отсортированном порядке, и каждая запись в дереве может быть найдена с использованием алгоритма, похожего на бинарный поиск, занимая в среднем логарифмическое время. Вставка и удаление также требуют в среднем логарифмического времени в бинарных деревьях поиска. Это может быть быстрее, чем линейное время вставки и удаления отсортированных массивов, и бинарные деревья сохраняют способность выполнять все операции, возможные на отсортированном массиве, включая диапазонные и приблизительные запросы. [22] [27]
Однако бинарный поиск обычно более эффективен для поиска, поскольку бинарные деревья поиска, скорее всего, будут неидеально сбалансированы, что приведет к немного худшей производительности, чем бинарный поиск. Это применимо даже к сбалансированным бинарным деревьям поиска , бинарным деревьям поиска, которые балансируют свои собственные узлы, потому что они редко производят дерево с наименьшим возможным количеством уровней. За исключением сбалансированных бинарных деревьев поиска, дерево может быть сильно несбалансированным с несколькими внутренними узлами с двумя потомками, что приводит к тому, что среднее и худшее время поиска приближается к сравнению. [e] Бинарные деревья поиска занимают больше места, чем отсортированные массивы. [29]
Двоичные деревья поиска подходят для быстрого поиска во внешней памяти, хранящейся на жестких дисках, поскольку двоичные деревья поиска могут быть эффективно структурированы в файловых системах. B-дерево обобщает этот метод организации дерева. B-деревья часто используются для организации долгосрочного хранения, такого как базы данных и файловые системы . [30] [31]
Хеширование
Для реализации ассоциативных массивов хэш-таблицы , структура данных, которая сопоставляет ключи с записями с помощью хэш-функции , обычно быстрее, чем бинарный поиск в отсортированном массиве записей. [32] Большинству реализаций хэш-таблиц в среднем требуется только амортизированное постоянное время. [f] [34] Однако хэширование бесполезно для приблизительных совпадений, таких как вычисление следующего наименьшего, следующего наибольшего и ближайшего ключа, поскольку единственная информация, предоставляемая при неудачном поиске, заключается в том, что цель отсутствует ни в одной записи. [35] Двоичный поиск идеально подходит для таких совпадений, выполняя их за логарифмическое время. Двоичный поиск также поддерживает приблизительные совпадения. Некоторые операции, такие как поиск наименьшего и наибольшего элемента, могут быть эффективно выполнены в отсортированных массивах, но не в хэш-таблицах. [22]
Установить алгоритмы членства
Связанная с поиском проблема — это членство в наборе . Любой алгоритм, который выполняет поиск, например, бинарный поиск, также может использоваться для членства в наборе. Существуют и другие алгоритмы, которые более конкретно подходят для членства в наборе. Битовый массив является самым простым, полезным, когда диапазон ключей ограничен. Он компактно хранит коллекцию битов , причем каждый бит представляет один ключ в диапазоне ключей. Битовые массивы очень быстры, требуя только времени. [36] Тип Judy1 массива Judy эффективно обрабатывает 64-битные ключи. [37]
Для получения приблизительных результатов фильтры Блума , другая вероятностная структура данных, основанная на хешировании, хранят набор ключей, кодируя ключи с помощью битового массива и нескольких хеш-функций. Фильтры Блума в большинстве случаев гораздо более эффективны с точки зрения пространства, чем битовые массивы, и не намного медленнее: с хеш-функциями запросы на членство требуют только времени. Однако фильтры Блума страдают от ложных срабатываний . [g] [h] [39]
Другие структуры данных
Существуют структуры данных, которые могут улучшить бинарный поиск в некоторых случаях как для поиска, так и для других операций, доступных для отсортированных массивов. Например, поиск, приблизительные совпадения и операции, доступные для отсортированных массивов, могут быть выполнены более эффективно, чем бинарный поиск в специализированных структурах данных, таких как деревья ван Эмде Боаса , деревья слияния , попытки и битовые массивы . Эти специализированные структуры данных обычно работают быстрее только потому, что они используют преимущества свойств ключей с определенным атрибутом (обычно ключей, которые являются небольшими целыми числами), и, таким образом, будут занимать много времени или места для ключей, у которых нет этого атрибута. [22] Пока ключи могут быть упорядочены, эти операции всегда могут быть выполнены по крайней мере эффективно в отсортированном массиве независимо от ключей. Некоторые структуры, такие как массивы Джуди, используют комбинацию подходов для смягчения этого, сохраняя при этом эффективность и возможность выполнять приблизительное совпадение. [37]
Вариации
Единый бинарный поиск

Равномерный бинарный поиск хранит вместо нижней и верхней границ разницу в индексе среднего элемента от текущей итерации до следующей итерации. Таблица поиска , содержащая разницы, вычисляется заранее. Например, если массив для поиска — [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] , то средний элемент ( ) будет 6. В этом случае средний элемент левого подмассива ( [1, 2, 3, 4, 5] ) — 3 , а средний элемент правого подмассива ( [7, 8, 9, 10, 11] ) — 9. Равномерный бинарный поиск будет хранить значение 3 , поскольку оба индекса отличаются от 6 на эту же величину. [40] Чтобы уменьшить пространство поиска, алгоритм либо добавляет, либо вычитает это изменение из индекса среднего элемента. Равномерный двоичный поиск может быть быстрее в системах, где вычисление средней точки неэффективно, например, на десятичных компьютерах . [41]
Экспоненциальный поиск

Экспоненциальный поиск расширяет бинарный поиск на неограниченные списки. Он начинается с поиска первого элемента с индексом, который является степенью двойки и больше целевого значения. После этого он устанавливает этот индекс в качестве верхней границы и переключается на бинарный поиск. Поиск занимает итерации до начала бинарного поиска и максимум итерации бинарного поиска, где — позиция целевого значения. Экспоненциальный поиск работает на ограниченных списках, но становится улучшением по сравнению с бинарным поиском только в том случае, если целевое значение находится вблизи начала массива. [42]
Интерполяционный поиск

Вместо вычисления средней точки, интерполяционный поиск оценивает положение целевого значения, принимая во внимание самые низкие и самые высокие элементы в массиве, а также длину массива. Он работает на основе того, что средняя точка не является лучшим предположением во многих случаях. Например, если целевое значение близко к самому высокому элементу в массиве, оно, скорее всего, будет расположено около конца массива. [43]
Распространенной функцией интерполяции является линейная интерполяция . Если — массив, — нижняя и верхняя границы соответственно, а — цель, то цель оценивается примерно как находящаяся между и . Когда используется линейная интерполяция, а распределение элементов массива равномерное или близкое к равномерному, поиск интерполяции выполняет сравнения. [43] [44] [45]
На практике интерполяционный поиск медленнее бинарного поиска для небольших массивов, поскольку интерполяционный поиск требует дополнительных вычислений. Его временная сложность растет медленнее, чем бинарный поиск, но это компенсирует только дополнительные вычисления для больших массивов. [43]
Дробное каскадирование
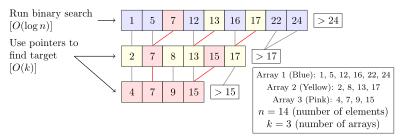
Дробное каскадирование — это метод, который ускоряет бинарный поиск одного и того же элемента в нескольких отсортированных массивах. Поиск каждого массива по отдельности требует времени, где — количество массивов. Дробное каскадирование сокращает это время за счет хранения в каждом массиве определенной информации о каждом элементе и его положении в других массивах. [46] [47]
Дробное каскадирование изначально было разработано для эффективного решения различных задач вычислительной геометрии . Дробное каскадирование применялось и в других местах, например, в добыче данных и маршрутизации интернет-протокола . [46]
Обобщение на графики
Двоичный поиск был обобщен для работы на определенных типах графов, где целевое значение хранится в вершине, а не в элементе массива. Двоичные деревья поиска являются одним из таких обобщений — когда запрашивается вершина (узел) в дереве, алгоритм либо узнает, что вершина является целью, либо, в противном случае, в каком поддереве будет находиться цель. Однако это можно обобщить еще больше следующим образом: учитывая неориентированный, положительно взвешенный граф и целевую вершину, алгоритм узнает при запросе вершины, что она равна цели, или ему дается инцидентное ребро, которое находится на кратчайшем пути от запрашиваемой вершины до цели. Стандартный алгоритм бинарного поиска — это просто случай, когда граф является путем. Аналогично, бинарные деревья поиска — это случай, когда ребра в левые или правые поддеревья задаются, когда запрашиваемая вершина не равна цели. Для всех неориентированных, положительно взвешенных графов существует алгоритм, который находит целевую вершину в запросах в худшем случае. [48]
Шумный бинарный поиск
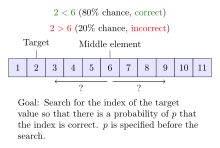
Шумные алгоритмы бинарного поиска решают случай, когда алгоритм не может надежно сравнить элементы массива. Для каждой пары элементов существует определенная вероятность того, что алгоритм сделает неправильное сравнение. Шумный бинарный поиск может найти правильное положение цели с заданной вероятностью, которая контролирует надежность полученного положения. Каждая шумная процедура бинарного поиска должна делать по крайней мере сравнений в среднем, где — функция бинарной энтропии , а — вероятность того, что процедура даст неправильное положение. [49] [50] [51] Проблему шумного бинарного поиска можно рассматривать как случай игры Реньи-Улама , [52] вариант Двадцати вопросов , где ответы могут быть неправильными. [53]
Квантовый бинарный поиск
Классические компьютеры ограничены худшим случаем точно итераций при выполнении бинарного поиска. Квантовые алгоритмы для бинарного поиска по-прежнему ограничены долей запросов (представляющих итерации классической процедуры), но постоянный множитель меньше единицы, что обеспечивает меньшую временную сложность на квантовых компьютерах . Любая точная квантовая процедура бинарного поиска — то есть процедура, которая всегда дает правильный результат — требует по крайней мере запросов в худшем случае, где — натуральный логарифм . [54] Существует точная квантовая процедура бинарного поиска, которая выполняется в запросах в худшем случае. [55] Для сравнения, алгоритм Гровера является оптимальным квантовым алгоритмом для поиска в неупорядоченном списке элементов, и он требует запросов. [56]
История
Идея сортировки списка элементов для ускорения поиска восходит к древности. Самым ранним известным примером была табличка Инакибит-Ану из Вавилона, датируемая примерно 200 г. до н. э . Табличка содержала около 500 шестидесятеричных чисел и их обратных чисел, отсортированных в лексикографическом порядке , что облегчало поиск определенной записи. Кроме того, на Эгейских островах было обнаружено несколько списков имен, отсортированных по первой букве . Католикон , латинский словарь, законченный в 1286 г. н. э., был первой работой, описывающей правила сортировки слов в алфавитном порядке, а не только по первым нескольким буквам. [9]
В 1946 году Джон Мочли впервые упомянул о двоичном поиске в рамках лекций школы Мура , основополагающего курса колледжа по информатике. [9] В 1957 году Уильям Уэсли Петерсон опубликовал первый метод интерполяционного поиска. [9] [57] Каждый опубликованный алгоритм двоичного поиска работал только для массивов, длина которых была на единицу меньше степени двойки [i] до 1960 года, когда Деррик Генри Лемер опубликовал алгоритм двоичного поиска, который работал со всеми массивами. [59] В 1962 году Герман Боттенбрух представил реализацию двоичного поиска на ALGOL 60 , которая помещала сравнение на равенство в конец, увеличивая среднее число итераций на одну, но уменьшая до одной число сравнений на итерацию. [8] Равномерный двоичный поиск был разработан А. К. Чандрой из Стэнфордского университета в 1971 году. [9] В 1986 году Бернар Шазелл и Леонидас Дж. Гибас представили дробное каскадирование как метод решения многочисленных задач поиска в вычислительной геометрии . [46] [60] [61]
Проблемы внедрения
Хотя основная идея бинарного поиска сравнительно проста, детали могут оказаться на удивление сложными.
— Дональд Кнут [2]
Когда Джон Бентли назначил бинарный поиск в качестве проблемы на курсе для профессиональных программистов, он обнаружил, что девяносто процентов не смогли предоставить правильное решение после нескольких часов работы над ним, в основном потому, что неправильные реализации не запускались или возвращали неправильный ответ в редких крайних случаях . [62] Исследование, опубликованное в 1988 году, показывает, что точный код для него можно найти только в пяти из двадцати учебников. [63] Кроме того, собственная реализация бинарного поиска Бентли, опубликованная в его книге 1986 года Programming Pearls , содержала ошибку переполнения , которая оставалась незамеченной более двадцати лет. Реализация бинарного поиска в библиотеке языка программирования Java имела ту же ошибку переполнения более девяти лет. [64]
В практической реализации переменные, используемые для представления индексов, часто будут иметь фиксированный размер (целые числа), и это может привести к арифметическому переполнению для очень больших массивов. Если середина диапазона вычисляется как , то значение может превышать диапазон целых чисел типа данных, используемого для хранения средней точки, даже если и находятся в пределах диапазона. Если и неотрицательны, этого можно избежать, вычислив среднюю точку как . [65]
Бесконечный цикл может возникнуть, если условия выхода из цикла определены неправильно. Если превышает , поиск не удался и необходимо сообщить об этом. Кроме того, цикл должен быть завершен, когда целевой элемент найден, или в случае реализации, где эта проверка перемещена в конец, должны быть проверки того, был ли поиск успешным или неудачным в конце. Бентли обнаружил, что большинство программистов, которые неправильно реализовали бинарный поиск, допустили ошибку в определении условий выхода. [8] [66]
Поддержка библиотеки
Стандартные библиотеки многих языков включают процедуры бинарного поиска:
- C предоставляет функцию
bsearch()в своей стандартной библиотеке , которая обычно реализуется с помощью бинарного поиска, хотя официальный стандарт этого не требует. [67] - Стандартная библиотека C++ предоставляет функции
binary_search(),lower_bound(),upper_bound()иequal_range(). [68] - Стандартная библиотека Phobos языка D в
std.rangeмодуле предоставляет типSortedRange(возвращаемый функциямиsort()иassumeSorted()) с методамиcontains(),equaleRange(),lowerBound()иtrisect(), которые по умолчанию используют методы бинарного поиска для диапазонов, предлагающих произвольный доступ. [69] - COBOL предоставляет
SEARCH ALLглагол для выполнения бинарного поиска в упорядоченных таблицах COBOL. [70] - Стандартный пакет библиотеки Go
sortсодержит функцииSearch,SearchInts,SearchFloat64s, иSearchStrings, которые реализуют общий двоичный поиск, а также специальные реализации для поиска фрагментов целых чисел, чисел с плавающей точкой и строк соответственно. [71] - Java предлагает набор перегруженных
binarySearch()статических методов в классахArraysиCollectionsв стандартномjava.utilпакете для выполнения двоичного поиска в массивах Java и вLists соответственно. [72] [73] - Microsoft .NET Framework 2.0 предлагает статические универсальные версии алгоритма бинарного поиска в своих базовых классах коллекций. Примером может служить
System.ArrayметодBinarySearch<T>(T[] array, T value). [74] - Для Objective-C метод предоставляется фреймворком Cocoa в
NSArray -indexOfObject:inSortedRange:options:usingComparator:Mac OS X 10.6+. [75] Фреймворк Core Foundation C от Apple также содержитCFArrayBSearchValues()функцию. [76] - Python предоставляет
bisectмодуль, который сохраняет список в отсортированном порядке без необходимости сортировать список после каждой вставки. [77] - Класс Array в Ruby
bsearchвключает метод со встроенным приблизительным сопоставлением. [78] - Примитивный срез Rust
binary_search()обеспечивает ,binary_search_by(),binary_search_by_key(), иpartition_point(). [79]
Смотрите также
- Метод бисекции – алгоритм нахождения нуля функции – та же идея, которая используется для решения уравнений в действительных числах.
- Мультипликативный бинарный поиск – вариация бинарного поиска с упрощенным вычислением средней точки
Примечания и ссылки
 Эта статья была отправлена в WikiJournal of Science для внешнего академического рецензирования в 2018 году (отчеты рецензентов). Обновленный контент был повторно интегрирован в страницу Википедии по лицензии CC-BY-SA-3.0 ( 2019 ). Версия записи, на которой она была проверена: Anthony Lin; et al. (2 июля 2019 г.). "Алгоритм бинарного поиска" (PDF) . WikiJournal of Science . 2 (1): 5. doi : 10.15347/WJS/2019.005 . ISSN 2470-6345. Wikidata Q81434400.
Эта статья была отправлена в WikiJournal of Science для внешнего академического рецензирования в 2018 году (отчеты рецензентов). Обновленный контент был повторно интегрирован в страницу Википедии по лицензии CC-BY-SA-3.0 ( 2019 ). Версия записи, на которой она была проверена: Anthony Lin; et al. (2 июля 2019 г.). "Алгоритм бинарного поиска" (PDF) . WikiJournal of Science . 2 (1): 5. doi : 10.15347/WJS/2019.005 . ISSN 2470-6345. Wikidata Q81434400.
Примечания
- ^ Это нотация Big O , а — логарифм . В нотации Big O основание логарифма не имеет значения, поскольку каждый логарифм данного основания является постоянным множителем другого логарифма другого основания. То есть, , где — константа.
- ^ Любой алгоритм поиска, основанный исключительно на сравнениях, можно представить с помощью бинарного дерева сравнения. Внутренний путь — это любой путь от корня до существующего узла. Пусть — длина внутреннего пути , сумма длин всех внутренних путей. Если каждый элемент с одинаковой вероятностью будет найден, то средний случай равен или просто единице плюс среднее значение всех длин внутренних путей дерева. Это происходит потому, что внутренние пути представляют элементы, которые алгоритм поиска сравнивает с целью. Длины этих внутренних путей представляют собой количество итераций после корневого узла. Добавление среднего значения этих длин к одной итерации в корне дает средний случай. Поэтому, чтобы минимизировать среднее количество сравнений, длина внутреннего пути должна быть минимизирована. Оказывается, что дерево для бинарного поиска минимизирует длину внутреннего пути. Кнут 1998 доказал, что длина внешнего пути (длина пути по всем узлам, где присутствуют оба потомка для каждого уже существующего узла) минимизируется, когда внешние узлы (узлы без потомков) лежат в пределах двух последовательных уровней дерева. Это также применимо к внутренним путям, поскольку длина внутреннего пути линейно связана с длиной внешнего пути . Для любого дерева узлов, . Когда каждое поддерево имеет одинаковое количество узлов, или, что эквивалентно, массив делится пополам в каждой итерации, внешние узлы, а также их внутренние родительские узлы лежат в пределах двух уровней. Из этого следует, что бинарный поиск минимизирует количество средних сравнений, поскольку его дерево сравнения имеет наименьшую возможную длину внутреннего пути. [14]
- ^ Кнут 1998 показал на своей компьютерной модели MIX , которую Кнут спроектировал как представление обычного компьютера, что среднее время выполнения этой вариации для успешного поиска составляет единиц времени по сравнению с единицами для обычного бинарного поиска. Временная сложность для этой вариации растет немного медленнее, но за счет более высокой начальной сложности. [18]
- ^ Кнут 1998 выполнил формальный анализ производительности по времени обоих этих алгоритмов поиска. На компьютере MIX Кнута , который Кнут спроектировал как представление обычного компьютера, двоичный поиск занимает в среднем единицы времени для успешного поиска, в то время как линейный поиск с контрольным узлом в конце списка занимает единицы. Линейный поиск имеет более низкую начальную сложность, поскольку он требует минимальных вычислений, но он быстро превосходит бинарный поиск по сложности. На компьютере MIX двоичный поиск превосходит линейный поиск с контрольным узлом только в том случае, если . [14] [23]
- ^ Вставка значений в отсортированном порядке или в чередующемся шаблоне ключей от самого низкого к самому высокому приведет к созданию бинарного дерева поиска, которое максимизирует среднее и наихудшее время поиска. [28]
- ^ Поиск в некоторых реализациях хэш-таблиц возможен за гарантированно постоянное время. [33]
- ^ Это связано с тем, что простая установка всех битов, на которые указывают хэш-функции для определенного ключа, может повлиять на запросы для других ключей, которые имеют общее расположение хэша для одной или нескольких функций. [38]
- ^ Существуют усовершенствования фильтра Блума, которые улучшают его сложность или поддерживают удаление; например, фильтр Cuckoo использует хеширование Cuckoo для получения этих преимуществ. [38]
- ^ То есть массивы длиной 1, 3, 7, 15, 31 ... [58]
Цитаты
- ^ Уильямс, младший, Луис Ф. (22 апреля 1976 г.). Модификация метода поиска половинного интервала (бинарного поиска). Труды 14-й конференции ACM Southeast. ACM. стр. 95–101. doi : 10.1145/503561.503582 . Архивировано из оригинала 12 марта 2017 г. . Получено 29 июня 2018 г. .
- ^ ab Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Бинарный поиск».
- ^ Баттерфилд и Нгонди 2016, с. 46.
- ^ Кормен и др. 2009, стр. 39.
- ^ Вайсштейн, Эрик В. «Двоичный поиск». MathWorld .
- ^ ab Флорес, Иван; Мадпис, Джордж (1 сентября 1971 г.). «Средняя длина двоичного поиска для плотных упорядоченных списков». Сообщения ACM . 14 (9): 602–603. doi : 10.1145/362663.362752 . ISSN 0001-0782. S2CID 43325465.
- ^ abc Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Алгоритм B».
- ^ abcd Bottenbruch, Hermann (1 апреля 1962 г.). «Структура и использование ALGOL 60». Journal of the ACM . 9 (2): 161–221. doi : 10.1145/321119.321120 . ISSN 0004-5411. S2CID 13406983.Процедура описана на стр. 214 (§43) под названием «Программа для двоичного поиска».
- ^ abcdef Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «История и библиография».
- ^ аб Касахара и Моришита 2006, стр. 8–9.
- ^ abc Sedgewick & Wayne 2011, §3.1, подраздел «Ранг и выбор».
- ^ abc Goldman & Goldman 2008, стр. 461–463.
- ^ Седжвик и Уэйн 2011, §3.1, подраздел «Запросы диапазона».
- ^ abcdefghijkl Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Дальнейший анализ бинарного поиска».
- ^ Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), «Теорема B».
- ^ Чанг 2003, стр. 169.
- ^ abc Knuth 1997, §2.3.4.5 («Длина пути»).
- ^ ab Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Упражнение 23».
- ^ Рольфе, Тимоти Дж. (1997). «Аналитический вывод сравнений в бинарном поиске». ACM SIGNUM Newsletter . 32 (4): 15–19. doi : 10.1145/289251.289255 . S2CID 23752485.
- ^ Куонг, Пол-Вирак; Морин, Пэт (2017). «Макет массива для поиска на основе сравнения». Журнал экспериментальной алгоритмики . 22. Статья 1.3. arXiv : 1509.05053 . doi : 10.1145/3053370. S2CID 23752485.
- ^ Кнут 1997, §2.2.2 («Последовательное распределение»).
- ^ abcd Бим, Пол; Фих, Фейт Э. (2001). «Оптимальные границы для проблемы предшественника и связанных с ней проблем». Журнал компьютерных и системных наук . 65 (1): 38–72. doi : 10.1006/jcss.2002.1822 .
- ^ Кнут 1998, Ответы на упражнения (§6.2.1) для «Упражнения 5».
- ^ Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»).
- ^ Кнут 1998, §5.3.1 («Сортировка по минимуму»).
- ^ Седжвик и Уэйн 2011, §3.2 («Упорядоченные таблицы символов»).
- ^ Седжвик и Уэйн 2011, §3.2 («Двоичные деревья поиска»), подраздел «Методы, основанные на порядке, и удаление».
- ^ Кнут 1998, §6.2.2 («Поиск в двоичном дереве»), подраздел «А как насчет наихудшего случая?».
- ^ Седжвик и Уэйн 2011, §3.5 («Приложения»), «Какую реализацию таблицы символов мне следует использовать?».
- ^ Кнут 1998, §5.4.9 («Диски и барабаны»).
- ^ Кнут 1998, §6.2.4 («Многоканальные деревья»).
- ^ Кнут 1998, §6.4 («Хеширование»).
- ^ Кнут 1998, §6.4 («Хеширование»), подраздел «История».
- ^ Дитцфельбингер, Мартин; Карлин, Анна ; Мельхорн, Курт ; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарьян, Роберт Э. (август 1994 г.). «Динамическое идеальное хеширование: верхняя и нижняя границы». SIAM Journal по вычислительной технике . 23 (4): 738–761. дои : 10.1137/S0097539791194094.
- ^ Морин, Пат. "Хэш-таблицы" (PDF) . стр. 1. Архивировано (PDF) из оригинала 9 октября 2022 г. Получено 28 марта 2016 г.
- ^ Кнут 2011, §7.1.3 («Побитовые приемы и методы»).
- ^ ab Silverstein, Alan, Judy IV shop manual (PDF) , Hewlett-Packard , стр. 80–81, архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ ab Fan, Bin; Andersen, Dave G.; Kaminsky, Michael; Mitzenmacher, Michael D. (2014). Фильтр Cuckoo: практически лучше, чем Bloom . Труды 10-й Международной конференции ACM по новым сетевым экспериментам и технологиям. стр. 75–88. doi : 10.1145/2674005.2674994 .
- ^ Блум, Бертон Х. (1970). «Пространственно-временные компромиссы в хэш-кодировании с допустимыми ошибками». Сообщения ACM . 13 (7): 422–426. CiteSeerX 10.1.1.641.9096 . doi :10.1145/362686.362692. S2CID 7931252.
- ^ Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Важная вариация».
- ^ Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Алгоритм U».
- ^ Моффат и Терпин 2002, стр. 33.
- ^ abc Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Интерполяционный поиск».
- ^ Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Упражнение 22».
- ^ Перл, Иегошуа; Итай, Алон; Авни, Хаим (1978). «Интерполяционный поиск — поиск log log n». Сообщения ACM . 21 (7): 550–553. doi : 10.1145/359545.359557 . S2CID 11089655.
- ^ abc Chazelle, Bernard ; Liu, Ding (6 июля 2001 г.). Нижние границы для поиска пересечений и дробного каскадирования в более высокой размерности. 33-й симпозиум ACM по теории вычислений . ACM. стр. 322–329. doi :10.1145/380752.380818. ISBN 978-1-58113-349-3. Получено 30 июня 2018 г.
- ^ Chazelle, Bernard ; Liu, Ding (1 марта 2004 г.). «Нижние границы для поиска пересечений и дробного каскадирования в более высокой размерности» (PDF) . Journal of Computer and System Sciences . 68 (2): 269–284. CiteSeerX 10.1.1.298.7772 . doi :10.1016/j.jcss.2003.07.003. ISSN 0022-0000. Архивировано (PDF) из оригинала 9 октября 2022 г. . Получено 30 июня 2018 г. .
- ^ Эмамджомех-Заде, Эхсан; Кемпе, Дэвид; Сингхал, Викрант (2016). Детерминированный и вероятностный бинарный поиск в графах . 48-й симпозиум ACM по теории вычислений . С. 519–532. arXiv : 1503.00805 . doi : 10.1145/2897518.2897656.
- ^ Бен-Ор, Майкл; Хассидим, Авинатан (2008). «Байесовский обучающийся алгоритм оптимален для зашумленного бинарного поиска (и довольно хорош для квантового)» (PDF) . 49-й симпозиум по основам компьютерной науки . стр. 221–230. doi :10.1109/FOCS.2008.58. ISBN 978-0-7695-3436-7. Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ Пелц, Анджей (1989). «Поиск с известной вероятностью ошибки». Теоретическая информатика . 63 (2): 185–202. doi : 10.1016/0304-3975(89)90077-7 .
- ^ Ривест, Рональд Л .; Мейер, Альберт Р.; Клейтман , Дэниел Дж .; Винклманн, К. Борьба с ошибками в процедурах бинарного поиска . 10-й симпозиум ACM по теории вычислений . doi : 10.1145/800133.804351 .
- ^ Пелц, Анджей (2002). «Поисковые игры с ошибками — пятьдесят лет борьбы с лжецами». Теоретическая информатика . 270 (1–2): 71–109. doi : 10.1016/S0304-3975(01)00303-6 .
- ^ Реньи, Альфред (1961). «Об одной задаче теории информации». Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei (на венгерском языке). 6 : 505–516. МР 0143666.
- ^ Хойер, Питер; Неербек, Ян; Ши, Яоюнь (2002). «Квантовые сложности упорядоченного поиска, сортировки и различия элементов». Algorithmica . 34 (4): 429–448. arXiv : quant-ph/0102078 . doi :10.1007/s00453-002-0976-3. S2CID 13717616.
- ^ Чайлдс, Эндрю М.; Ландаль, Эндрю Дж.; Паррило, Пабло А. (2007). «Квантовые алгоритмы для задачи упорядоченного поиска с помощью полуопределенного программирования». Physical Review A. 75 ( 3). 032335. arXiv : quant-ph/0608161 . Bibcode : 2007PhRvA..75c2335C. doi : 10.1103/PhysRevA.75.032335. S2CID 41539957.
- ^ Гровер, Лов К. (1996). Быстрый квантово-механический алгоритм поиска в базе данных . 28-й симпозиум ACM по теории вычислений . Филадельфия, Пенсильвания. С. 212–219. arXiv : quant-ph/9605043 . doi : 10.1145/237814.237866.
- ^ Петерсон, Уильям Уэсли (1957). «Адресация для памяти с произвольным доступом». IBM Journal of Research and Development . 1 (2): 130–146. doi :10.1147/rd.12.0130.
- ^ "2 n −1". OEIS A000225 Архивировано 8 июня 2016 года на Wayback Machine . Получено 7 мая 2016 года.
- ^ Лемер, Деррик (1960). «Обучение компьютера комбинаторным трюкам». Труды симпозиумов по прикладной математике . 10 : 180–181. doi : 10.1090/psapm/010 . ISBN 9780821813102.
- ^ Шазель, Бернар ; Гибас, Леонидас Дж. (1986). «Дробное каскадирование: I. Метод структурирования данных» (PDF) . Algorithmica . 1 (1–4): 133–162. CiteSeerX 10.1.1.117.8349 . doi :10.1007/BF01840440. S2CID 12745042.
- ^ Шазель, Бернар ; Гибас, Леонидас Дж. (1986), «Дробное каскадирование: II. Приложения» (PDF) , Algorithmica , 1 (1–4): 163–191, doi :10.1007/BF01840441, S2CID 11232235
- ^ Бентли 2000, §4.1 («Проблема бинарного поиска»).
- ^ Паттис, Ричард Э. (1988). «Ошибки учебника в бинарном поиске». Бюллетень SIGCSE . 20 : 190–194. doi :10.1145/52965.53012.
- ^ Блох, Джошуа (2 июня 2006 г.). «Дополнительно, дополнительно – прочтите все об этом: почти все бинарные поиски и сортировки слиянием сломаны». Блог Google Research . Архивировано из оригинала 1 апреля 2016 г. Получено 21 апреля 2016 г.
- ^ Руджиери, Сальваторе (2003). «О вычислении полусуммы двух целых чисел» (PDF) . Information Processing Letters . 87 (2): 67–71. CiteSeerX 10.1.1.13.5631 . doi :10.1016/S0020-0190(03)00263-1. Архивировано (PDF) из оригинала 3 июля 2006 г. . Получено 19 марта 2016 г. .
- ^ Бентли 2000, §4.4 («Принципы»).
- ^ "bsearch – бинарный поиск в отсортированной таблице". The Open Group Base Specifications (7-е изд.). The Open Group . 2013. Архивировано из оригинала 21 марта 2016 г. Получено 28 марта 2016 г.
- ^ Страуструп 2013, стр. 945.
- ^ "std.range - Язык программирования D". dlang.org . Получено 29 апреля 2020 г. .
- ^ Unisys (2012), Справочное руководство по программированию на языке COBOL ANSI-85 , т. 1, стр. 598–601
- ^ "Package sort". Язык программирования Go . Архивировано из оригинала 25 апреля 2016 года . Получено 28 апреля 2016 года .
- ^ "java.util.Arrays". Java Platform Standard Edition 8 Documentation . Oracle Corporation . Архивировано из оригинала 29 апреля 2016 года . Получено 1 мая 2016 года .
- ^ "java.util.Collections". Java Platform Standard Edition 8 Documentation . Oracle Corporation . Архивировано из оригинала 23 апреля 2016 года . Получено 1 мая 2016 года .
- ^ "List<T>.BinarySearch method (T)". Microsoft Developer Network . Архивировано из оригинала 7 мая 2016 . Получено 10 апреля 2016 .
- ^ "NSArray". Библиотека разработчиков Mac . Apple Inc. Архивировано из оригинала 17 апреля 2016 года . Получено 1 мая 2016 года .
- ^ "CFArray". Библиотека разработчиков Mac . Apple Inc. Архивировано из оригинала 20 апреля 2016 года . Получено 1 мая 2016 года .
- ^ "8.6. bisect — Алгоритм деления массива пополам". Стандартная библиотека Python . Python Software Foundation. Архивировано из оригинала 25 марта 2018 г. Получено 26 марта 2018 г.
- ^ Фицджеральд 2015, стр. 152.
- ^ "Primitive Type slice". The Rust Standard Library . The Rust Foundation. 2024. Получено 25 мая 2024 .
Источники
- Бентли, Джон (2000). Жемчужины программирования (2-е изд.). Эддисон-Уэсли . ISBN 978-0-201-65788-3.
- Баттерфилд, Эндрю; Нгонди, Джерард Э. (2016). Словарь компьютерных наук (7-е изд.). Оксфорд, Великобритания: Oxford University Press . ISBN 978-0-19-968897-5.
- Чанг, Ши-Куо (2003). Структуры данных и алгоритмы . Программная инженерия и инженерия знаний. Том 13. Сингапур: World Scientific . ISBN 978-981-238-348-8.
- Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009). Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 978-0-262-03384-8.
- Фицджеральд, Майкл (2015). Справочник по карману Ruby . Севастополь, Калифорния: O'Reilly Media . ISBN 978-1-4919-2601-7.
- Голдман, Салли А.; Голдман, Кеннет Дж. (2008). Практическое руководство по структурам данных и алгоритмам с использованием Java . Бока-Ратон, Флорида: CRC Press . ISBN 978-1-58488-455-2.
- Касахара, Масахиро; Морисита, Шиничи (2006). Крупномасштабная обработка геномной последовательности . Лондон, Великобритания: Imperial College Press. ISBN 978-1-86094-635-6.
- Кнут, Дональд (1997). Фундаментальные алгоритмы . Искусство программирования . Том 1 (3-е изд.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89683-1.
- Кнут, Дональд (1998). Сортировка и поиск . Искусство программирования . Том 3 (2-е изд.). Рединг, Массачусетс: Addison-Wesley Professional. ISBN 978-0-201-89685-5.
- Кнут, Дональд (2011). Комбинаторные алгоритмы . Искусство программирования . Том 4A (1-е изд.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-03804-0.
- Моффат, Алистер; Турпин, Эндрю (2002). Алгоритмы сжатия и кодирования . Гамбург, Германия: Kluwer Academic Publishers. doi :10.1007/978-1-4615-0935-6. ISBN 978-0-7923-7668-2.
- Седжвик, Роберт ; Уэйн, Кевин (2011). Алгоритмы (4-е изд.). Верхняя Сэддл-Ривер, Нью-Джерси: Addison-Wesley Professional. ISBN 978-0-321-57351-3.Сокращенная веб-версия
 ; книжная версия
; книжная версия .
. - Страуструп, Бьярне (2013). Язык программирования C++ (4-е изд.). Upper Saddle River, Нью-Джерси: Addison-Wesley Professional. ISBN 978-0-321-56384-2.
Внешние ссылки
- Словарь алгоритмов и структур данных NIST: бинарный поиск
- Сравнения и тесты различных реализаций бинарного поиска на языке C Архивировано 25 сентября 2019 г. на Wayback Machine






















![{\displaystyle [1,2,3,4,4,5,6,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d3a10b0250aafff08cc862bc99b5f3b4f7c33f3)

![{\displaystyle [1,2,4,4,4,5,6,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5867073891e85c24ad16f2e0df8a93bd487cdec3)













![{\displaystyle [20,30,40,50,80,90,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2a762c441505aff6153082ad4c7863a26f52962)
























![{\displaystyle E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edbb46592a2cfed4a5d626d6080fd530bf7693b5)









































