Модель камеры-обскуры

Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Февраль 2008 ) ( Узнайте, как и когда удалять это сообщение )

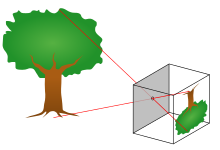
Модель камеры-обскуры описывает математическую связь между координатами точки в трехмерном пространстве и ее проекцией на плоскость изображения идеальной камеры -обскуры , где апертура камеры описывается как точка, и линзы не используются для фокусировки света. Модель не включает, например, геометрические искажения или размытие несфокусированных объектов, вызванные линзами и апертурами конечного размера. ^[1] Она также не учитывает, что большинство практических камер имеют только дискретные координаты изображения. Это означает, что модель камеры-обскуры может использоваться только как приближение первого порядка отображения трехмерной сцены в двумерное изображение . Ее достоверность зависит от качества камеры и, в общем случае, уменьшается от центра изображения к краям по мере увеличения эффектов искажения линзы.

Некоторые эффекты, которые модель камеры-обскуры не учитывает, можно компенсировать, например, применяя подходящие преобразования координат к координатам изображения; другие эффекты достаточно малы, чтобы ими можно было пренебречь, если используется высококачественная камера. Это означает, что модель камеры-обскуры часто можно использовать в качестве разумного описания того, как камера отображает 3D-сцену, например, в компьютерном зрении и компьютерной графике .

Геометрия , связанная с отображением камеры-обскуры, проиллюстрирована на рисунке. Рисунок содержит следующие основные объекты:

• Трехмерная ортогональная система координат с началом в точке O. Там же находится апертура камеры . Три оси системы координат обозначаются как X1, X2, X3. Ось X3 указывает в направлении обзора камеры и называется оптической осью , главной осью или главным лучом . Плоскость, охватываемая осями X1 и X2, является передней стороной камеры или главной плоскостью .
• Плоскость изображения, где трехмерный мир проецируется через апертуру камеры. Плоскость изображения параллельна осям X1 и X2 и расположена на расстоянии от начала координат O в отрицательном направлении оси X3, где f — фокусное расстояние камеры-обскуры. Практическая реализация камеры-обскуры подразумевает, что плоскость изображения расположена таким образом, что пересекает ось X3 в точке с координатой -f , где f > 0 .${\displaystyle f}$
• Точка R на пересечении оптической оси и плоскости изображения. Эта точка называется главной точкой ^[2] или центром изображения .
• Точка P где-то в мире с координатами относительно осей X1, X2 и X3.${\displaystyle (x_{1},x_{2},x_{3})}$
• Линия проекции точки P в камеру. Это зеленая линия, которая проходит через точку P и точку O.
• Проекция точки P на плоскость изображения, обозначенная Q. Эта точка задается пересечением линии проекции (зеленой) и плоскости изображения. В любой практической ситуации мы можем предположить, что > 0, что означает, что точка пересечения хорошо определена.${\displaystyle x_{3}}$
• В плоскости изображения также имеется двумерная система координат с началом в точке R и осями Y1 и Y2, параллельными X1 и X2 соответственно. Координаты точки Q относительно этой системы координат равны .${\displaystyle (y_{1},y_{2})}$

Отверстие - обскура камеры, через которое должны проходить все линии проекции, предполагается бесконечно малым, точкой. В литературе эта точка в трехмерном пространстве называется оптическим (или линзовым, или камерным) центром . ^[3]

Далее мы хотим понять, как координаты точки Q зависят от координат точки P. Это можно сделать с помощью следующего рисунка, на котором показана та же сцена, что и на предыдущем рисунке, но теперь сверху, глядя вниз в отрицательном направлении оси X2.${\displaystyle (y_{1},y_{2})}$${\displaystyle (x_{1},x_{2},x_{3})}$

На этом рисунке мы видим два подобных треугольника , оба из которых имеют части проекционной линии (зеленые) в качестве гипотенуз . Катеты левого треугольника равны и , а катеты прямоугольного треугольника равны и . Поскольку два треугольника подобны, следует, что${\displaystyle -y_{1}}$${\displaystyle x_{1}}$${\displaystyle x_{3}}$

${\displaystyle {\frac {-y_{1}}{f}}={\frac {x_{1}}{x_{3}}}}$или${\displaystyle y_{1}=-{\frac {f\,x_{1}}{x_{3}}}}$

Аналогичное исследование, рассматривая отрицательное направление оси X1, дает

${\displaystyle {\frac {-y_{2}}{f}}={\frac {x_{2}}{x_{3}}}}$или${\displaystyle y_{2}=-{\frac {f\,x_{2}}{x_{3}}}}$

Это можно резюмировать следующим образом:

${\displaystyle {\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}}=-{\frac {f}{x_{3}}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}}$

что представляет собой выражение, описывающее связь между трехмерными координатами точки P и ее координатами изображения, заданными точкой Q в плоскости изображения.${\displaystyle (x_{1},x_{2},x_{3})}$${\displaystyle (y_{1},y_{2})}$

Отображение координат 3D в 2D, описываемое камерой-обскуром, представляет собой перспективную проекцию с последующим поворотом на 180° в плоскости изображения. Это соответствует тому, как работает настоящая камера-обскура; полученное изображение поворачивается на 180°, а относительный размер проецируемых объектов зависит от их расстояния до фокальной точки, а общий размер изображения зависит от расстояния f между плоскостью изображения и фокальной точкой. Для того чтобы создать не повернутое изображение, чего мы и ожидаем от камеры, есть две возможности:

• Повернуть систему координат в плоскости изображения на 180° (в любом направлении). Именно так любая практическая реализация камеры-обскуры решила бы эту проблему; для фотографической камеры мы поворачиваем изображение перед тем, как посмотреть на него, а для цифровой камеры мы считываем пиксели в таком порядке, чтобы оно стало повернутым.
• Разместите плоскость изображения так, чтобы она пересекала ось X3 в точке f, а не в точке -f, и переделайте предыдущие вычисления. Это сгенерирует виртуальную (или фронтальную) плоскость изображения , которую невозможно реализовать на практике, но которая обеспечивает теоретическую камеру, анализ которой может быть проще, чем реальной.

В обоих случаях результирующее отображение трехмерных координат в двухмерные координаты изображения задается выражением выше, но без отрицания, таким образом

${\displaystyle {\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}}={\frac {f}{x_{3}}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}}$

Отображение 3D-координат точек в пространстве в 2D-координаты изображения также может быть представлено в однородных координатах . Пусть будет представлением 3D-точки в однородных координатах (4-мерный вектор), а пусть будет представлением изображения этой точки в камере-обскуре (3-мерный вектор). Тогда справедливо следующее соотношение${\displaystyle \mathbf {x} }$${\displaystyle \mathbf {y} }$

${\displaystyle \mathbf {y} \sim \mathbf {C} \,\mathbf {x} }$

где — матрица камеры , а означает равенство между элементами проективных пространств . Это подразумевает, что левая и правая стороны равны с точностью до ненулевого скалярного умножения. Следствием этого отношения является то, что также может рассматриваться как элемент проективного пространства ; две матрицы камеры эквивалентны, если они равны с точностью до скалярного умножения. Это описание отображения камеры-обскуры как линейного преобразования, а не как дроби двух линейных выражений, позволяет упростить многие выводы соотношений между трехмерными и двумерными координатами. ^{[ необходима цитата ]}${\displaystyle \mathbf {C} }$${\displaystyle 3\times 4}$ ${\displaystyle \,\сим }$${\displaystyle \mathbf {C} }$${\displaystyle \mathbf {C} }$

• Резекция камеры
• Уравнение коллинеарности
• Входной зрачок — эквивалентное расположение отверстия по отношению к пространству объектов в реальной камере.
• Выходной зрачок — эквивалентное расположение отверстия по отношению к плоскости изображения в реальной камере.
• Ибн аль-Хайсам
• Пинхол-камера , практическая реализация математической модели, описанной в этой статье.
• Прямолинейная линза

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Pinhole camera model" – news · newspapers · books · scholar · JSTOR (January 2008) (Learn how and when to remove this message)

• Дэвид А. Форсайт и Жан Понс (2003). Компьютерное зрение, современный подход . Prentice Hall. ISBN 0-12-379777-2.
• Ричард Хартли и Эндрю Зиссерман (2003). Многомерная геометрия в компьютерном зрении. Cambridge University Press. ISBN 0-521-54051-8.
• Бернд Йене (1997). Практическое руководство по обработке изображений для научных приложений . CRC Press. ISBN 0-8493-8906-2.
• Линда Г. Шапиро и Джордж К. Стокман (2001). Компьютерное зрение . Prentice Hall. ISBN 0-13-030796-3.
• Gang Xu и Zhengyou Zhang (1996). Эпиполярная геометрия в стерео, движении и распознавании объектов. Kluwer Academic Publishers. ISBN 0-7923-4199-6.
• Селиски, Ричард (2022). Компьютерное зрение: алгоритмы и приложения (2-е изд.). Springer Nature. стр. 925. ISBN 3030343723. Получено 30 декабря 2023 г. .