Гемореология
Эта статья может потребовать очистки для соответствия стандартам качества Википедии . Конкретная проблема: статья полна дублирующейся информации в разных разделах. ( Декабрь 2020 ) |
Гемореология , также пишется как гемореология ( haemo от греч. 'αἷμα, haima ' кровь '; и rheology от греч. ῥέω rhéō ' течение ' и -λoγία, -logia 'изучение'), или реология крови , является изучением реологических свойств крови и ее элементов плазмы и клеток . Правильная перфузия тканей может происходить только тогда, когда реологические свойства крови находятся в определенных пределах. Изменения этих свойств играют важную роль в процессах заболевания. [1] Вязкость крови определяется вязкостью плазмы, гематокритом (объемной долей эритроцитов, которые составляют 99,9% клеточных элементов) и механическими свойствами эритроцитов . Эритроциты обладают уникальным механическим поведением, которое можно обсудить в терминах деформируемости эритроцитов и агрегации эритроцитов . [2] Из-за этого кровь ведет себя как неньютоновская жидкость . Таким образом, вязкость крови меняется в зависимости от скорости сдвига . Кровь становится менее вязкой при высоких скоростях сдвига, таких как те, которые возникают при увеличенном потоке, например, во время упражнений или в пиковую систолу . Поэтому кровь является жидкостью , разжижающейся при сдвиге . Напротив, вязкость крови увеличивается, когда скорость сдвига уменьшается с увеличением диаметра сосудов или при низком потоке, например, ниже по течению от препятствия или в диастолу . Вязкость крови также увеличивается с увеличением агрегационной способности эритроцитов.
Вязкость крови
Вязкость крови является мерой сопротивления крови течению. Ее также можно описать как густоту и липкость крови. Это биофизическое свойство делает ее критически важным фактором трения о стенки сосудов , скорости венозного возврата , работы, необходимой сердцу для перекачивания крови, и того, сколько кислорода транспортируется к тканям и органам. Эти функции сердечно -сосудистой системы напрямую связаны с сосудистым сопротивлением , преднагрузкой , постнагрузкой и перфузией соответственно. [ требуется цитата ]
Основными факторами, определяющими вязкость крови, являются гематокрит , деформируемость эритроцитов , агрегация эритроцитов и вязкость плазмы . Вязкость плазмы определяется содержанием воды и макромолекулярными компонентами, поэтому факторами, влияющими на вязкость крови, являются концентрация белка плазмы и типы белков в плазме. [3] Тем не менее, гематокрит оказывает самое сильное влияние на вязкость цельной крови. Увеличение гематокрита на одну единицу может вызвать увеличение вязкости крови до 4%. [2] Эта связь становится все более чувствительной по мере увеличения гематокрита. Когда гематокрит повышается до 60 или 70%, что часто происходит при полицитемии , [4] вязкость крови может стать в 10 раз больше, чем у воды, и ее поток по кровеносным сосудам значительно замедляется из-за повышенного сопротивления потоку. [5] Это приведет к снижению доставки кислорода . [6] Другие факторы, влияющие на вязкость крови, включают температуру , где повышение температуры приводит к снижению вязкости. Это особенно важно при гипотермии , когда повышение вязкости крови приводит к проблемам с кровообращением.
Клиническое значение
Многие традиционные факторы риска сердечно-сосудистых заболеваний независимо связаны с вязкостью цельной крови.
| Факторы риска сердечно-сосудистых заболеваний независимо связаны с вязкостью цельной крови [7] |
|---|
| Гипертония |
| Общий холестерин |
| ЛПОНП-холестерин |
| ЛПНП-холестерин |
| Холестерин ЛПВП (отрицательная корреляция) |
| Триглицериды |
| Хиломикроны |
| Сахарный диабет и инсулинорезистентность |
| Метаболический синдром |
| Ожирение |
| курение сигарет |
| Мужской пол |
| Возраст |
Анемия может снизить вязкость крови, что может привести к сердечной недостаточности . [7] Кроме того, повышение вязкости плазмы коррелирует с прогрессированием заболеваний коронарных и периферических артерий . [3] [4]
Нормальный уровень
В паскаль - секундах (Па·с) вязкость крови при температуре 37 °C обычно составляет от 3 × 10−3 до 4 × 10−3 [ 8] соответственно 3–4 сантипуаз (сП) в системе единиц сантиметр-грамм-секунда .
,
где - плотность. Вязкость крови можно измерить с помощью вискозиметров, способных проводить измерения при различных скоростях сдвига, например, ротационного вискозиметра . [9]
Вязкоупругость крови
Кровь является вязкоупругой жидкостью, что означает, что она обладает как вязкими, так и текучими характеристиками. Вязкий компонент возникает в основном из-за вязкости плазмы крови, в то время как упругий компонент возникает из-за деформации эритроцитов . Когда сердце сокращается, механическая энергия передается от сердца к крови; небольшая часть энергии рассеивается вязкостью суспензии , другая часть сохраняется в виде упругой энергии в эритроцитах, а оставшаяся энергия используется для приведения в действие кровообращения и, таким образом, преобразуется в кинетическую энергию . Вязкоупругие жидкости составляют более широкий класс жидкостей, называемых неньютоновскими жидкостями .
Эритроциты занимают около половины объема крови и обладают упругими свойствами. Это упругое свойство является самым большим фактором, способствующим вязкоупругому поведению крови. Большой объемный процент эритроцитов при нормальном уровне гематокрита оставляет мало места для движения и деформации клеток без взаимодействия с соседней клеткой. Расчеты показали, что максимальный объемный процент эритроцитов без деформации составляет 58%, что находится в диапазоне нормально встречающихся уровней. [10] Из-за ограниченного пространства между эритроцитами очевидно, что для того, чтобы кровь текла, существенное взаимодействие клеток будет играть ключевую роль. Это взаимодействие и тенденция клеток к агрегации являются основным фактором, способствующим вязкоупругому поведению крови. Деформация и агрегация эритроцитов также связаны с вызванными потоком изменениями в расположении и ориентации как третьим основным фактором ее вязкоупругого поведения. [11] [12] Другими факторами, способствующими вязкоупругим свойствам крови, являются вязкость плазмы, состав плазмы, температура и скорость потока или скорость сдвига. В совокупности эти факторы делают кровь человека вязкоупругой , неньютоновской и тиксотропной . [ 13]
Когда эритроциты находятся в состоянии покоя или при очень малых скоростях сдвига, они имеют тенденцию агрегировать и складывать вместе энергетически выгодным образом. Притяжение объясняется заряженными группами на поверхности клеток и наличием фибриногена и глобулинов. [14] Эта агрегированная конфигурация представляет собой расположение клеток с наименьшим количеством деформации. При очень низких скоростях сдвига вязкоупругие свойства крови доминируют за счет агрегации, а деформируемость клеток относительно незначительна. По мере увеличения скорости сдвига размер агрегатов начинает уменьшаться. При дальнейшем увеличении скорости сдвига клетки будут перестраиваться и ориентироваться, чтобы обеспечить каналы для прохождения плазмы и скольжения клеток. В этом диапазоне низких и средних скоростей сдвига клетки покачиваются относительно соседних клеток, обеспечивая поток. Влияние свойств агрегации на вязкоупругость уменьшается, а влияние деформируемости эритроцитов начинает увеличиваться. По мере того, как скорости сдвига становятся большими, эритроциты будут растягиваться или деформироваться и выравниваться с потоком. Образуются слои клеток, разделенные плазмой, и поток теперь приписывается слоям клеток, скользящим по слоям плазмы. Клеточный слой обеспечивает более легкий поток крови, и, таким образом, снижается вязкость и эластичность. Вязкоупругость крови определяется деформируемостью эритроцитов.
модель Максвелла
Модель Максвелла касается жидкостей Максвелла или материала Максвелла . Материал в модели Максвелла является жидкостью , что означает, что он соблюдает свойства непрерывности для консервативных уравнений: жидкости являются подмножеством фаз вещества и включают жидкости, газы, плазму и, в некоторой степени, пластичные твердые тела. Модель Максвелла создана для оценки локальных консервативных значений вязкоупругости с помощью глобальной меры в интегральном объеме модели, которая должна быть транспонирована в различные ситуации потока. Кровь является сложным материалом, в котором различные клетки, такие как эритроциты, прерывисты в плазме. Их размер и форма также нерегулярны, поскольку они не являются идеальными сферами. Усложняя более того форму объема крови, эритроциты не одинаково распределены в объеме образца крови, поскольку они мигрируют с градиентами скорости в направлении областей с самой высокой скоростью, вызывая известное представление эффекта Фореуса-Линдквиста , агрегируют или разделяются в оболочечных или пробковых потоках, описанных Терстоном. [15] Обычно модель Максвелла, описанная ниже, однородно рассматривает материал (однородный синий цвет) как идеально распределенную жидкость с частицами по всему объему (синего цвета), но Терстон показывает, что пачки красных клеток, пробки, больше присутствуют в области высокой скорости, если y является направлением высоты на рисунке модели Максвелла ( y ~H), а в области более низкой скорости есть слой свободных клеток ( y ~0), что означает, что фаза плазменной жидкости, которая деформируется в модели Максвелла, деформируется в соответствии с внутренними оболочками, которые полностью выходят за рамки аналитической модели Максвелла. [ необходима ссылка ]
Теоретически жидкость в модели Максвелла ведет себя точно так же в любой другой геометрии потока, например, в трубах, вращающихся ячейках или в состоянии покоя. Но на практике свойства крови меняются в зависимости от геометрии, и кровь показала себя неподходящим материалом для изучения в качестве жидкости в здравом смысле. Таким образом, модель Максвелла дает тенденции, которые должны быть завершены в реальной ситуации, за которой следует модель Терстона [15] в сосуде относительно распределения клеток в потоках оболочки и пробки. [ необходима цитата ]
Если рассматривать небольшой кубический объем крови, на который действуют силы, возникающие при работе сердца и сдвигающие силы от границ, то изменение формы куба будет иметь 2 компонента:
- Упругая деформация, которая восстанавливается и сохраняется в структуре крови.
- Проскальзывание, связанное с непрерывным притоком вязкой энергии.
При снятии силы куб частично восстановится. Упругая деформация обратима, а проскальзывание — нет. Это объясняет, почему упругая часть заметна только в нестационарном потоке. В стационарном потоке проскальзывание будет продолжать увеличиваться, а измерения неизменяющейся во времени силы будут игнорировать вклад упругости.

Рисунок 1 можно использовать для расчета следующих параметров, необходимых для оценки состояния крови при приложении силы.
- Напряжение сдвига:
- Деформация сдвига:
- Скорость сдвига:
Синусоидальный поток, изменяющийся во времени, используется для моделирования пульсации сердца. Вязкоупругий материал, подвергаемый воздействию потока, изменяющегося во времени, приведет к изменению фазы между и представленному как . Если , материал является чисто упругим, поскольку напряжение и деформация находятся в фазе, так что реакция одного, вызванная другим, является немедленной. Если = 90°, материал является чисто вязким, поскольку деформация отстает от напряжения на 90 градусов. Вязкоупругий материал будет где-то между 0 и 90 градусами.
Синусоидальное изменение во времени пропорционально . Таким образом, соотношение размера и фазы между напряжением, деформацией и скоростью сдвига описывается с помощью этого соотношения и радианной частоты, где — частота в герцах .
- Напряжение сдвига:
- Деформация сдвига:
- Скорость сдвига:
Компоненты комплексного касательного напряжения можно записать в виде:
Где - вязкое напряжение, а - упругое напряжение. Комплексный коэффициент вязкости можно найти, взяв отношение комплексного напряжения сдвига к комплексной скорости сдвига: [16]
Аналогично, комплексный динамический модуль G можно получить, взяв отношение комплексного напряжения сдвига к комплексной деформации сдвига.
Связывая уравнения с обычными вязкоупругими терминами, получаем модуль накопления G' и модуль потерь G".

Вязкоупругая модель материала Максвелла обычно используется для представления вязкоупругих свойств крови . Она использует чисто вязкий демпфер и чисто упругую пружину, соединенные последовательно. Анализ этой модели дает комплексную вязкость в терминах постоянной демпфера и постоянной пружины.
Модель Oldroyd-B
Одной из наиболее часто используемых конститутивных моделей для вязкоупругости крови является модель Oldroyd-B. Существует несколько вариаций неньютоновской модели Oldroyd-B, характеризующих поведение разжижения при сдвиге из-за агрегации и дисперсии эритроцитов при низкой скорости сдвига. Здесь мы рассматриваем трехмерную модель Oldroyd-B в сочетании с уравнением импульса и тензором полного напряжения. [17] Используется неньютоновский поток, который гарантирует, что вязкость крови является функцией диаметра сосуда d и гематокрита h. В модели Oldroyd-B соотношение между тензором напряжения сдвига B и тензором ориентационного напряжения A задается следующим образом:
где D/Dt — производная материала, V — скорость жидкости, C1, C2, g — константы. S и B определяются следующим образом:
Вязкоупругость эритроцитов
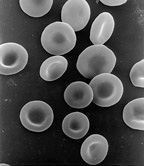
Эритроциты подвергаются интенсивной механической стимуляции как со стороны кровотока, так и со стороны стенок сосудов, и их реологические свойства важны для их эффективности в выполнении своих биологических функций в микроциркуляции. [18] Было показано, что сами по себе эритроциты проявляют вязкоупругие свойства. Существует несколько методов, используемых для исследования механических свойств эритроцитов, таких как:
- аспирация микропипеткой [19]
- микроотступ
- оптический пинцет
- высокочастотные электрические деформационные испытания
Эти методы работали над тем, чтобы охарактеризовать деформируемость эритроцитов с точки зрения сдвига, изгиба, модулей расширения площади и времени релаксации. [20] Однако они не смогли исследовать вязкоупругие свойства. Были реализованы другие методы, такие как фотоакустические измерения. Этот метод использует одноимпульсный лазерный луч для генерации фотоакустического сигнала в тканях, и измеряется время затухания сигнала. Согласно теории линейной вязкоупругости, время затухания равно соотношению вязкости и упругости, и поэтому можно получить характеристики вязкоупругости эритроцитов. [21]
Другой экспериментальный метод, используемый для оценки вязкоупругости, состоял в использовании ферромагнитных бусин, прикрепленных к поверхности клеток. Затем к магнитной бусинке прикладывались силы с использованием оптической магнитной скручивающей цитометрии, что позволило исследователям изучить зависящие от времени реакции эритроцитов. [22]
— механический крутящий момент на единицу объема шарика (единицы напряжения), который определяется по формуле:
где H — приложенное магнитное скручивающее поле, — угол магнитного момента бусины относительно исходного направления намагничивания, а c — постоянная бусины, которая находится в ходе экспериментов, проводимых путем помещения бусины в жидкость с известной вязкостью и приложения скручивающего поля.
Комплексный динамический модуль G можно использовать для представления соотношений между колебательным напряжением и деформацией:
где - модуль накопления , а - модуль потерь :
где и — амплитуды напряжения и деформации, а — сдвиг фаз между ними.

Из приведенных выше соотношений компоненты комплексного модуля определяются из петли, которая создается путем сравнения изменения крутящего момента с изменением времени, которое образует петлю при графическом представлении. Пределы петли - d(t) и площадь, A, ограниченная петлей - d(t), которая представляет собой рассеивание энергии за цикл, используются в расчетах. Фазовый угол , модуль накопления G' и модуль потерь G тогда становятся:
где d — смещение.
Гистерезис, показанный на рисунке 3, представляет собой вязкоупругость, присутствующую в эритроцитах. Неясно, связано ли это с молекулярными колебаниями мембраны или метаболической активностью, контролируемой внутриклеточной концентрацией АТФ . Необходимы дальнейшие исследования, чтобы полностью изучить это взаимодействие и пролить свет на основные характеристики вязкоупругой деформации эритроцитов.
Эффекты кровеносных сосудов
При рассмотрении вязкоупругого поведения крови in vivo необходимо также учитывать влияние артерий , капилляров и вен . Вязкость крови оказывает основное влияние на поток в более крупных артериях, в то время как эластичность, которая заключается в упругой деформируемости эритроцитов, оказывает основное влияние в артериолах и капиллярах. [23] Понимание распространения волн в стенках артерий, локальной гемодинамики и градиента напряжения сдвига стенки важно для понимания механизмов сердечно-сосудистой функции. Стенки артерий анизотропны и неоднородны, состоят из слоев с различными биомеханическими характеристиками, что делает понимание механического влияния, которое артерии вносят на кровоток, очень сложным. [24]
Медицинские причины для лучшего понимания
С медицинской точки зрения важность изучения вязкоупругих свойств крови становится очевидной. С развитием сердечно-сосудистых протезных устройств, таких как сердечные клапаны и насосы крови, требуется понимание пульсирующего потока крови в сложных геометриях. Несколько конкретных примеров - эффекты вязкоупругости крови и их значение для тестирования пульсирующих насосов крови. [25] Были задокументированы сильные корреляции между вязкоупругостью крови и региональным и глобальным мозговым кровотоком во время сердечно-легочного шунтирования. [26]
Это также привело к разработке аналога крови для изучения и тестирования протезных устройств. Классический аналог глицерина и воды обеспечивает хорошее представление вязкости и инерционных эффектов, но не имеет упругих свойств настоящей крови. Одним из таких аналогов крови является водный раствор ксантановой камеди и глицерина, разработанный для соответствия как вязким, так и упругим компонентам комплексной вязкости крови. [27]
Нормальные эритроциты деформируются, но многие состояния, такие как серповидноклеточная анемия , снижают их эластичность, что делает их менее деформируемыми. Эритроциты с пониженной деформируемостью имеют повышенное сопротивление потоку, что приводит к увеличению агрегации эритроцитов и снижению насыщения кислородом, что может привести к дальнейшим осложнениям. Наличие клеток с пониженной деформируемостью, как в случае серповидноклеточной анемии, имеет тенденцию подавлять образование плазменных слоев, и путем измерения вязкоупругости можно количественно определить степень ингибирования. [28]
История
В ранних теоретических работах кровь рассматривалась как неньютоновская вязкая жидкость. Первоначальные исследования оценивали кровь во время стационарного течения, а позднее — с использованием осциллирующего течения. [29] Профессор Джордж Б. Терстон из Техасского университета впервые представил идею о том, что кровь является вязкоупругой в 1972 году. Предыдущие исследования, которые изучали кровь в стационарном течении, показали незначительные упругие свойства, поскольку упругий режим сохраняется в крови во время начала течения, и поэтому его присутствие скрыто, когда течение достигает стационарного состояния. Ранние исследования использовали свойства, обнаруженные в стационарном течении, для получения свойств для ситуаций нестационарного течения. [30] [31] Достижения в области медицинских процедур и устройств требовали лучшего понимания механических свойств крови. [ необходима цитата ]
Уравнения состояния
Соотношения между напряжением сдвига и скоростью сдвига для крови должны быть определены экспериментально и выражены с помощью конститутивных уравнений . Учитывая сложное макрореологическое поведение крови, неудивительно, что одно уравнение не может полностью описать эффекты различных реологических переменных (например, гематокрита , скорости сдвига). Таким образом, существует несколько подходов к определению этих уравнений, некоторые из которых являются результатом подгонки экспериментальных данных, а другие основаны на конкретной реологической модели.
- Модель ньютоновской жидкости , где вязкость постоянна при всех скоростях сдвига. Этот подход справедлив для высоких скоростей сдвига ( ), где диаметр сосуда намного больше, чем клетки крови. [32]
- Модель жидкости Бингама учитывает агрегацию эритроцитов при низких скоростях сдвига. Поэтому она действует как упругое твердое тело при пороговом уровне напряжения сдвига, известном как предел текучести .
- Модель Эйнштейна, где η 0 — ньютоновская вязкость суспензионной жидкости, «k» — константа, зависящая от формы частиц, а H — объемная доля суспензии, занимаемая частицами. Это уравнение применимо для суспензий с низкой объемной долей частиц. Эйнштейн показал k=2,5 для сферических частиц.
- Модель Кассона, где "a" и "b" являются константами; при очень низких скоростях сдвига b является пределом текучести при сдвиге. Однако для крови экспериментальные данные не могут быть подогнаны под все скорости сдвига с помощью только одного набора констант "a" и "b", тогда как достаточно хорошее соответствие возможно путем применения уравнения к нескольким диапазонам скоростей сдвига и получения таким образом нескольких наборов констант.
- Модель Quemada, где k 0 , k ∞ и γ c являются константами. Это уравнение точно соответствует данным крови в очень широком диапазоне скоростей сдвига.
Другие характеристики
Эффект Фореуса
Открытие того, что для крови, текущей стабильно в трубках с диаметром менее 300 микрометров, средний гематокрит крови в трубке меньше гематокрита крови в резервуаре, питающем трубку, известно как эффект Фареуса. Этот эффект возникает в длине концентрационного входа трубки, в которой эритроциты движутся к центральной области трубки по мере их движения вниз по течению. Эта длина входа оценивается примерно в расстояние, которое кровь проходит за четверть секунды для крови, где агрегация эритроцитов незначительна, а диаметр сосуда больше примерно 20 микрометров. [1]
Эффект Фареуса-Линдквиста
Поскольку характерный размер канала потока приближается к размеру частиц в суспензии, следует ожидать, что простая континуальная модель суспензии окажется неприменимой. Часто этот предел применимости континуальной модели начинает проявляться при характерных размерах канала, которые примерно в 30 раз превышают диаметр частицы: в случае крови с характерным размером эритроцита 8 мкм очевидный сбой происходит примерно при 300 микрометрах. Это было продемонстрировано Фареусом и Линдквистом, которые обнаружили, что кажущаяся вязкость крови является функцией диаметра трубки для диаметров 300 микрометров и меньше, когда они пропускали кровь с постоянным гематокритом из хорошо перемешиваемого резервуара через трубку. Вывод о том, что для небольших трубок с диаметрами менее примерно 300 микрометров и для более высоких скоростей потока, которые не допускают заметной агрегации эритроцитов, эффективная вязкость крови зависит от диаметра трубки, известен как эффект Фареуса–Линдквиста. [1]
Смотрите также
- Альфред Л. Копли
- Кровавый молот
- Биореология , изучение реологических свойств (реологии) биологических жидкостей.
- Гемодинамика
- Синдром гипервязкости
- Руло — это конфигурация, которую принимают агрегаты эритроцитов.
Ссылки
- ^ abc Baskurt, OK; Hardeman M; Rampling MW; Meiselman HJ (2007). Справочник по гемореологии и гемодинамике . Амстердам, Нидерланды: IOS Press. С. 455. ISBN 978-1586037710. ISSN 0929-6743.
{{cite book}}:|journal=проигнорировано ( помощь ) - ^ ab Baskurt OK, Meiselman HJ (2003). «Реология крови и гемодинамика». Семинары по тромбозу и гемостазу . 29 (5): 435– 450. doi :10.1055/s-2003-44551. PMID 14631543. S2CID 17873138.
- ^ аб Кесмарки Г., Кеньерес П., Рабай М., Тот К. (2008). «Вязкость плазмы: забытая переменная». Клин. Гемореол. Микроциркулятор . 39 ( 1–4 ): 243–6 . doi : 10.3233/CH-2008-1088. PMID 18503132. Архивировано из оригинала 14 мая 2016 г.
- ^ ab Tefferi A (май 2003 г.). «Современный подход к диагностике и лечению истинной полицитемии». Curr. Hematol. Rep . 2 (3): 237–41 . PMID 12901345.
- ^ Lenz C, Rebel A, Waschke KF, Koehler RC, Frietsch T (2008). «Вязкость крови модулирует перфузию тканей: иногда и где-то». Transfus Altern Transfus Med . 9 (4): 265– 272. doi :10.1111/j.1778-428X.2007.00080.x. PMC 2519874. PMID 19122878 .
- ^ Kwon O, Krishnamoorthy M, Cho YI, Sankovic JM, Banerjee RK (февраль 2008 г.). «Влияние вязкости крови на транспорт кислорода в остаточной стенозированной артерии после ангиопластики». Журнал биомеханической инженерии . 130 (1): 011003. doi :10.1115/1.2838029. PMID 18298179. S2CID 40266740.
- ^ ab Jeong, Seul-Ki; et al. (апрель 2010 г.). «Сердечно-сосудистые риски коррекции анемии с помощью эритроцитстимулирующих агентов: следует ли контролировать вязкость крови для оценки риска?». Cardiovascular Drugs and Therapy . 24 (2): 151– 60. doi :10.1007/s10557-010-6239-7. PMID 20514513. S2CID 6366788.
- ^ Элерт, Гленн (27 ноября 2021 г.). «Вязкость». Гипертекстовая книга по физике – через physics.info.
- ^ Baskurt OK, Boynard M, Cokelet GC и др. (2009). «Новые рекомендации по гемореологическим лабораторным методам». Клиническая гемореология и микроциркуляция . 42 (2): 75–97 . doi :10.3233/CH-2009-1202. PMID 19433882. S2CID 15866651.
- ^ А. Бертон (1965). Физиология и биофизика кровообращения . Чикаго (США): Year Book Medical Publisher Inc. стр. 53.
- ^ G. Thurston; Nancy M. Henderson (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746 . PMID 17148856.
- ^ G. Thurston (1989). «Выделение плазмы – теория клеточного наслаивания для кровотока». Биореология . 26 (2): 199– 214. doi :10.3233/bir-1989-26208. PMID 2605328.
- ^ G. Thurston (1979). «Реологические параметры вязкости, вязкоупругости и тиксотропии крови». Биореология . 16 (3): 149– 162. doi :10.3233/bir-1979-16303. PMID 508925.
- ^ Л. Пиркл и Т. Боднар, Численное моделирование кровотока с использованием обобщенной модели Олдройда-Б, Европейская конференция по вычислительной гидродинамике, 2010 г.
- ^ ab Thurston G., Henderson Nancy M. (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746 . PMID 17148856.
- ^ Т. Хау, Достижения в гемодинамике и гемореологии, т. 1, JAI Press LTD., 1996, 1-32.
- ^ Р. Берд, Р. Армстронг, О. Хассагер, Динамика полимерных жидкостей; Механика жидкости, 1987, 2, 493 - 496
- ^ М. Мофрад, Х. Кархер и Р. Камм, Механика цитоскелета: модели и измерения, 2006, 71-83
- ^ В. Лубарда и А. Марцани, Вязкоупругий ответ тонких мембран применительно к эритроцитам, Acta Mechanica, 2009, 202, 1–16
- ^ Д. Федосов, Б. Касвелл и Г. Карниадакис, Крупнозернистая модель эритроцитов с точными механическими свойствами, реологией и динамикой, 31-я ежегодная международная конференция IEEE EMBS, Миннеаполис, Миннесота, 2009 г.
- ^ J. Li, Z. Tang, Y. Xia, Y. Lou и G. Li, Вязкоупругие характеристики клеток с использованием фотоакустических измерений, Журнал прикладной физики, 2008, 104
- ^ М. Маринкович, К. Тернер, Дж. Батлер, Дж. Фредберг и С. Суреш, Вязкоупругость эритроцитов человека, Американский журнал физиологии. Физиология клетки 2007, 293, 597-605.
- ^ А. Ундар, В. Вон и Дж. Калхун, Влияние сердечно-легочного шунтирования и глубокой гипотермической остановки кровообращения на вязкоупругость крови и мозговой кровоток в модели неонатального поросенка, Perfusion 2000, 15, 121–128
- ^ S. Canic , J. Tambaca, G. Guidoboni, A. Mikelic, C Hartley и D Rosenstrauch, Моделирование вязкоупругого поведения артериальных стенок и их взаимодействие с пульсирующим кровотоком, Журнал прикладной математики, 2006, 67, 164–193
- ^ J. Long, A. Undar, K. Manning и S. Deutsch, Вязкоупругость детской крови и ее значение для тестирования пульсирующего детского насоса крови, Американское общество внутренних органов, 2005, 563 - 566
- ^ А. Ундар и В. Вон, Влияние умеренного гипотермического сердечно-легочного шунтирования на вязкоупругость крови у пациентов, перенесших аортокоронарное шунтирование, Искусственные органы 26(11), 964–966
- ^ К. Брукшир и Дж. Тарбелл, Оценка прозрачной жидкости-аналога крови: водная ксантановая камедь/глицерин, Биореология, 1993, 2, 107-116
- ^ G. Thurston, N. Henderson и M. Jeng, Влияние переливания эритроцитафереза на вязкоупругость крови с серповидноклеточной анемией, Clinical Hemorheology and Microcirculation 30 (2004) 61–75
- ^ Дж. Уомерсли, Метод расчета скорости, расхода и вязкого сопротивления в артериях при известном градиенте давления, Американский журнал физиологии, 1955, 127, 553-563.
- ^ Г. Терстон, Вязкоупругость человеческой крови, Biophysical Journal, 1972, 12, 1205–1217.
- ^ Г. Терстон, Вязкость и вязкоупругость крови в трубках малого диаметра, Микрососудистые исследования, 1975, 11, 133-146.
- ^ Фанг, YC (1993). Биомеханика: механические свойства живых тканей (2-е изд.). Нью-Йорк, Нью-Йорк: Springer. ISBN 9780387979472.



























![{\displaystyle S+\gamma \left[{\frac {DS}{Dt}}-\Delta V\cdot SS\cdot {(\Delta V)}^{T}\right]=\mu (h,d)\left[B+\gamma \left({\frac {DB}{Dt}}-\Delta V\cdot BB\cdot {(\Delta V)}^{T}\right)\right]-gA+C_{1}\left(gA-{\frac {C_{2}I}{\mu (h,d)^{2}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3831dced9bb1d3f7ab7e680931a46882db0817cd)



















