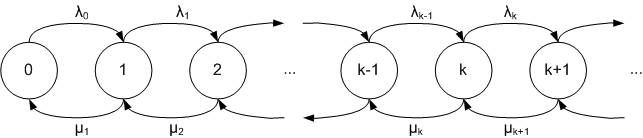
Процесс рождения–смерти

Процесс рождения–смерти (или процесс рождения и смерти ) является особым случаем непрерывного во времени марковского процесса , в котором переходы состояний бывают только двух типов: «рождения», которые увеличивают переменную состояния на единицу, и «смерти», которые уменьшают состояние на единицу. Он был введен Уильямом Феллером . ^[1] Название модели происходит от общего применения, использования таких моделей для представления текущего размера популяции, где переходы являются буквальными рождениями и смертями. Процессы рождения–смерти имеют множество приложений в демографии , теории очередей , инженерии производительности , эпидемиологии , биологии и других областях. Они могут использоваться, например, для изучения эволюции бактерий , числа людей с заболеванием в популяции или числа покупателей в очереди в супермаркете.

Когда происходит рождение, процесс переходит из состояния n в состояние n  + 1. Когда происходит смерть, процесс переходит из состояния n в состояние  n  − 1. Процесс определяется положительными показателями рождаемости и положительными показателями смертности . Количество особей в процессе в момент времени обозначается как . Процесс обладает свойством Маркова и описывает, как изменяется со временем. Для малых предполагается, что функция удовлетворяет следующим свойствам:${\displaystyle \{\lambda _{i}\}_{i=0\точки \infty}}$${\displaystyle \{\mu _{i}\}_{i=1\dots \infty }}$${\displaystyle т}$${\displaystyle X(т)}$${\displaystyle P_{i,j}(t)={\mathsf {P}}\{X(t+s)=j|X(s)=i\}}$${\displaystyle X(т)}$${\displaystyle \треугольник т>0}$${\displaystyle P_{i,j}(\треугольник t)}$

${\displaystyle P_{i,i+1}(\triangle t)=\lambda _{i}\triangle t+o(\triangle t),\quad i\geq 0,}$

${\displaystyle P_{i,i-1}(\triangle t)=\mu _{i}\triangle t+o(\triangle t),\quad i\geq 1,}$

${\displaystyle P_{i,i}(\triangle t)=1-(\lambda _{i}+\mu _{i})\triangle t+o(\triangle t),\quad i\geq 1.}$

Этот процесс представлен на следующем рисунке, где состояния процесса (т. е. количество особей в популяции) изображены кружками, а переходы между состояниями обозначены стрелками.

О повторяемости и неустойчивости в марковских процессах см. раздел 5.3 из «Цепи Маркова» .

Условия повторяемости и мимолетности были установлены Сэмюэлем Карлином и Джеймсом МакГрегором . ^[2]

Процесс рождения и смерти повторяется тогда и только тогда, когда

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\ инфти .}$

Процесс рождения и смерти является эргодическим тогда и только тогда, когда

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{and}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}<\infty .}$

Процесс рождения и смерти является нуль-рекуррентным тогда и только тогда, когда

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{and}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}=\infty .}$

Используя расширенный тест Бертрана (см. раздел 4.1.4 из теста отношения ), можно вывести условия повторяемости, транзитивности, эргодичности и нулевой повторяемости в более явной форме. ^[3]

Для целых чисел обозначим -ю итерацию натурального логарифма , т.е. и для любого , .${\displaystyle K\geq 1,}$${\displaystyle \ln _{(K)}(x)}$${\displaystyle К}$${\displaystyle \ln _{(1)}(x)=\ln(x)}$${\displaystyle 2\leq k\leq K}$${\displaystyle \ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))}$

Тогда условия повторяемости и мимолетности процесса рождения и смерти таковы.

Процесс рождения и смерти является преходящим, если существуют и таковы, что для всех${\displaystyle с>1,}$ ${\displaystyle K\geq 1}$${\displaystyle n_{0}}$${\displaystyle n>n_{0}}$

${\displaystyle {\frac {\lambda _{n}}{\mu _{n}}}\geq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K-1}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}+{\frac {c}{n\prod _{j=1}^{K}\ln _{(j)}(n)}},}$

где пустая сумма предполагается равной 0.${\displaystyle К=1}$

Процесс рождения и смерти является повторяющимся, если существуют и такие, что для всех${\displaystyle K\geq 1}$${\displaystyle n_{0}}$${\displaystyle n>n_{0}}$

${\displaystyle {\frac {\lambda _{n}}{\mu _{n}}}\leq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}.}$

Более широкие классы процессов рождения и смерти, для которых могут быть установлены условия повторяемости и преходящести, можно найти в ^{[4] .}

Рассмотрим одномерное случайное блуждание , которое определяется следующим образом. Пусть , и где принимает значения , а распределение определяется следующими условиями:${\displaystyle S_{t},\ t=0,1,\ldots ,}$${\displaystyle S_{0}=1}$${\displaystyle S_{t}=S_{t-1}+e_{t},\ t\geq 1,}$${\displaystyle e_{t}}$${\displaystyle \pm 1}$${\displaystyle S_{t}}$

${\displaystyle {\mathsf {P}}\{S_{t+1}=S_{t}+1|S_{t}>0\}={\frac {1}{2}}+{\frac {\alpha _{S_{t}}}{S_{t}}},\quad {\mathsf {P}}\{S_{t+1}=S_{t}-1|S_{t}>0\}={\frac {1}{2}}-{\frac {\alpha _{S_{t}}}{S_{t}}},\quad {\mathsf {P}}\{S_{t+1}=1|S_{t}=0\}=1,}$

где удовлетворяют условию .${\displaystyle \alpha _{n}}$${\displaystyle 0<\alpha _{n}<\min\{C,n/2\},C>0}$

Случайное блуждание, описанное здесь, является дискретным во времени аналогом процесса рождения и смерти (см. цепь Маркова ) с коэффициентами рождаемости

${\displaystyle \lambda _{n}={\frac {1}{2}}+{\frac {\alpha _{n}}{n}},}$

и уровень смертности

${\displaystyle \mu _{n}={\frac {1}{2}}-{\frac {\alpha _{n}}{n}}}$.

Таким образом, повторяемость или скоротечность случайного блуждания связана с повторяемостью или скоротечностью процесса рождения и смерти. ^[3]

Случайное блуждание является преходящим, если существуют , и такие, что для всех${\displaystyle c>1}$${\displaystyle K\geq 1}$${\displaystyle n_{0}}$${\displaystyle n>n_{0}}$

${\displaystyle \alpha _{n}\geq {\frac {1}{4}}\left(1+\sum _{k=1}^{K-1}\prod _{j=1}^{k}{\frac {1}{\ln _{(j)}(n)}}+c\prod _{j=1}^{K}{\frac {1}{\ln _{(j)}(n)}}\right),}$

где пустая сумма для предполагается равной нулю.${\displaystyle K=1}$

Случайное блуждание является рекуррентным, если существуют и такие, что для всех${\displaystyle K\geq 1}$${\displaystyle n_{0}}$${\displaystyle n>n_{0}}$

${\displaystyle \alpha _{n}\leq {\frac {1}{4}}\left(1+\sum _{k=1}^{K}\prod _{j=1}^{k}{\frac {1}{\ln _{(j)}(n)}}\right).}$

Если процесс рождения и смерти эргодичен, то существуют стационарные вероятности , где — вероятность того, что процесс рождения и смерти находится в состоянии в момент времени Предел существует независимо от начальных значений и вычисляется с помощью соотношений:${\displaystyle \pi _{k}=\lim _{t\to \infty }p_{k}(t),}$${\displaystyle p_{k}(t)}$${\displaystyle k}$${\displaystyle t.}$${\displaystyle p_{k}(0),}$

${\displaystyle \pi _{k}=\pi _{0}\prod _{i=1}^{k}{\frac {\lambda _{i-1}}{\mu _{i}}},\quad k=1,2,\ldots ,}$

${\displaystyle \pi _{0}={\frac {1}{1+\sum _{k=1}^{\infty }\prod _{i=1}^{k}{\frac {\lambda _{i-1}}{\mu _{i}}}}}.}$

Эти предельные вероятности получаются из бесконечной системы дифференциальных уравнений для${\displaystyle p_{k}(t):}$

${\displaystyle p_{0}^{\prime }(t)=\mu _{1}p_{1}(t)-\lambda _{0}p_{0}(t)\,}$

${\displaystyle p_{k}^{\prime }(t)=\lambda _{k-1}p_{k-1}(t)+\mu _{k+1}p_{k+1}(t)-(\lambda _{k}+\mu _{k})p_{k}(t),k=1,2,\ldots ,\,}$

и начальное состояние${\displaystyle \sum _{k=0}^{\infty }p_{k}(t)=1.}$

В свою очередь, последняя система дифференциальных уравнений выводится из системы разностных уравнений , описывающих динамику системы за малое время . В течение этого малого времени рассматриваются только три типа переходов: одна смерть, или одно рождение, или отсутствие рождения и смерти. Вероятность первых двух из этих переходов имеет порядок . Другие переходы в течение этого малого интервала, такие как более одного рождения , или более одной смерти , или по крайней мере одно рождение и по крайней мере одна смерть, имеют вероятности, которые имеют меньший порядок, чем , и, следовательно, пренебрежимо малы при выводах. Если система находится в состоянии k , то вероятность рождения в течение интервала равна , вероятность смерти равна , а вероятность отсутствия рождения и смерти равна . Для процесса популяции «рождение» — это переход к увеличению численности популяции на 1, тогда как «смерть» — это переход к уменьшению численности популяции на 1.${\displaystyle \Delta t}$${\displaystyle \Delta t}$ ${\displaystyle \Delta t}$${\displaystyle \Delta t}$ ${\displaystyle \Delta t}$${\displaystyle \Delta t}$${\displaystyle \lambda _{k}\Delta t+o(\Delta t)}$${\displaystyle \mu _{k}\Delta t+o(\Delta t)}$${\displaystyle 1-\lambda _{k}\Delta t-\mu _{k}\Delta t+o(\Delta t)}$

Чистый процесс рождения – это процесс рождения-смерти, где для всех .${\displaystyle \mu _{i}=0}$${\displaystyle i\geq 0}$

Чистый процесс смерти — это процесс рождения-смерти, где для всех .${\displaystyle \lambda _{i}=0}$${\displaystyle i\geq 0}$

Модели M/M/1 и M/M/c , обе используемые в теории очередей , представляют собой процессы рождения и смерти, используемые для описания клиентов в бесконечной очереди.

Процессы рождения-смерти используются в филодинамике в качестве априорного распределения для филогений , то есть двоичного дерева, в котором события рождения соответствуют ветвям дерева, а события смерти соответствуют узлам листьев. ^[5] В частности, они используются в вирусной филодинамике ^[6] для понимания процесса передачи и того, как число инфицированных людей меняется с течением времени. ^[7]

Использование обобщенных процессов рождения-смерти в филодинамике стимулировало исследования степени, в которой показатели рождаемости и смертности могут быть идентифицированы из данных. ^[8] Хотя модель в целом неидентифицируема, подмножество моделей, которые обычно используются, идентифицируемы. ^[9]

В теории очередей процесс рождения–смерти является наиболее фундаментальным примером модели очередей , очередь M/M/C/K/ /FIFO${\displaystyle \infty }$ (в полной нотации Кендалла ). Это очередь с пуассоновскими прибытиями , взятая из бесконечной популяции, и C серверами с экспоненциально распределенным временем обслуживания с K местами в очереди. Несмотря на предположение о бесконечной популяции, эта модель является хорошей моделью для различных телекоммуникационных систем.

M /M/1 — это очередь с одним сервером и бесконечным размером буфера. В неслучайной среде процесс рождения–смерти в моделях очередей имеет тенденцию быть долгосрочными средними, поэтому средняя скорость прибытия задается как , а среднее время обслуживания как . Процесс рождения и смерти — это очередь M/M/1, когда,${\displaystyle \lambda }$${\displaystyle 1/\mu }$

${\displaystyle \lambda _{i}=\lambda {\text{ and }}\mu _{i}=\mu {\text{ for all }}i.\,}$

Дифференциальные уравнения для вероятности того, что система находится в состоянии k в момент времени t, имеют вид

${\displaystyle p_{0}^{\prime }(t)=\mu p_{1}(t)-\lambda p_{0}(t),\,}$

${\displaystyle p_{k}^{\prime }(t)=\lambda p_{k-1}(t)+\mu p_{k+1}(t)-(\lambda +\mu )p_{k}(t)\quad {\text{for }}k=1,2,\ldots \,}$

Чистый процесс рождения с является частным случаем процесса очередей M/M/1. У нас есть следующая система дифференциальных уравнений :${\displaystyle \lambda _{k}\equiv \lambda }$

${\displaystyle p_{0}^{\prime }(t)=-\lambda p_{0}(t),\,}$

${\displaystyle p_{k}^{\prime }(t)=\lambda p_{k-1}(t)-\lambda p_{k}(t)\quad {\text{for }}k=1,2,\ldots \,}$

При начальном условии и решение системы имеет вид${\displaystyle p_{0}(0)=1}$${\displaystyle p_{k}(0)=0,\ k=1,2,\ldots }$

${\displaystyle p_{k}(t)={\frac {(\lambda t)^{k}}{k!}}\mathrm {e} ^{-\lambda t}.}$

То есть (однородный) пуассоновский процесс — это чистый процесс рождения.

M/M/C — это многосерверная очередь с серверами C и бесконечным буфером. Она характеризуется следующими параметрами рождения и смерти:

${\displaystyle \mu _{i}=i\mu \quad {\text{ for }}i\leq C-1,\,}$

и

${\displaystyle \mu _{i}=C\mu \quad {\text{ for }}i\geq C,\,}$

с

${\displaystyle \lambda _{i}=\lambda \quad {\text{ for all }}i.\,}$

Система дифференциальных уравнений в этом случае имеет вид:

${\displaystyle p_{0}^{\prime }(t)=\mu p_{1}(t)-\lambda p_{0}(t),\,}$

${\displaystyle p_{k}^{\prime }(t)=\lambda p_{k-1}(t)+(k+1)\mu p_{k+1}(t)-(\lambda +k\mu )p_{k}(t)\quad {\text{for }}k=1,2,\ldots ,C-1,\,}$

${\displaystyle p_{k}^{\prime }(t)=\lambda p_{k-1}(t)+C\mu p_{k+1}(t)-(\lambda +C\mu )p_{k}(t)\quad {\text{for }}k\geq C.\,}$

Чистый процесс смерти с является частным случаем процесса очередей M/M/C. У нас есть следующая система дифференциальных уравнений :${\displaystyle \mu _{k}=k\mu }$

${\displaystyle p_{C}^{\prime }(t)=-C\mu p_{C}(t),\,}$

${\displaystyle p_{k}^{\prime }(t)=(k+1)\mu p_{k+1}(t)-k\mu p_{k}(t)\quad {\text{for }}k=0,1,\ldots ,C-1.\,}$

При начальном условии и получаем решение${\displaystyle p_{C}(0)=1}$${\displaystyle p_{k}(0)=0,\ k=0,1,\ldots ,C-1,}$

${\displaystyle p_{k}(t)={\binom {C}{k}}\mathrm {e} ^{-k\mu t}\left(1-\mathrm {e} ^{-\mu t}\right)^{C-k},}$

который представляет собой версию биномиального распределения в зависимости от временного параметра (см. Биномиальный процесс ).${\displaystyle t}$

Очередь M/M/1/K — это односерверная очередь с буфером размера K. Эта очередь имеет применение в телекоммуникациях, а также в биологии, когда популяция имеет предельную емкость. В телекоммуникациях мы снова используем параметры из очереди M/M/1 с,

${\displaystyle \lambda _{i}=\lambda \quad {\text{ for }}0\leq i<K,\,}$

${\displaystyle \lambda _{i}=0\quad {\text{ for }}i\geq K,\,}$

${\displaystyle \mu _{i}=\mu \quad {\text{ for }}1\leq i\leq K.\,}$

В биологии, особенно в росте бактерий, когда популяция равна нулю, нет возможности расти, поэтому,

${\displaystyle \lambda _{0}=0.\,}$

Кроме того, если емкость представляет собой предел, при котором особь умирает от перенаселения,

${\displaystyle \mu _{K}=0.\,}$

Дифференциальные уравнения для вероятности того, что система находится в состоянии k в момент времени t, имеют вид

${\displaystyle p_{0}^{\prime }(t)=\mu p_{1}(t)-\lambda p_{0}(t),}$

${\displaystyle p_{k}^{\prime }(t)=\lambda p_{k-1}(t)+\mu p_{k+1}(t)-(\lambda +\mu )p_{k}(t)\quad {\text{ for }}k\leq K-1,\,}$

${\displaystyle p_{K}^{\prime }(t)=\lambda p_{K-1}(t)-(\lambda +\mu )p_{K}(t),\,}$

${\displaystyle p_{k}(t)=0\quad {\text{ for }}k>K.\,}$

Говорят, что очередь находится в равновесии, если существуют вероятности стационарного состояния . Условием существования этих вероятностей стационарного состояния в случае очереди M/M/1 является , а в случае очереди M/M/C — . Параметр обычно называют параметром нагрузки или параметром утилизации . Иногда его также называют интенсивностью трафика .${\displaystyle \pi _{k}=\lim _{t\to \infty }p_{k}(t),\ k=0,1,\ldots ,}$${\displaystyle \rho =\lambda /\mu <1}$${\displaystyle \rho =\lambda /(C\mu )<1}$${\displaystyle \rho }$

Используя в качестве примера очередь M/M/1, уравнения устойчивого состояния имеют вид

${\displaystyle \lambda \pi _{0}=\mu \pi _{1},\,}$

${\displaystyle (\lambda +\mu )\pi _{k}=\lambda \pi _{k-1}+\mu \pi _{k+1}.\,}$

Это можно свести к

${\displaystyle \lambda \pi _{k}=\mu \pi _{k+1}{\text{ for }}k\geq 0.\,}$

Итак, принимая во внимание, что , получаем${\displaystyle \pi _{0}+\pi _{1}+\ldots =1}$

${\displaystyle \pi _{k}=(1-\rho )\rho ^{k}.}$

Двусторонний процесс рождения и смерти определяется аналогично стандартному, с той лишь разницей, что коэффициенты рождаемости и смертности определяются для значений индексного параметра . ^[10] После этого двусторонний процесс рождения и смерти является рекуррентным тогда и только тогда, когда${\displaystyle \lambda _{i}}$${\displaystyle \mu _{i}}$${\displaystyle i=0,\pm 1,\pm 2,\ldots }$

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{and}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{-n}}{\mu _{-n}}}=\infty .}$

Понятия эргодичности и нулевой повторяемости определяются аналогичным образом путем расширения соответствующих понятий стандартного процесса рождения и смерти.

• единица Эрланга
• Теория массового обслуживания
• Модели очередей
• Процесс квазирождения–смерти
• процесс Морана

• Латуш, Г.; Рамасвами, В. (1999). «Процессы квазирождения и смерти». Введение в матричные аналитические методы в стохастическом моделировании (1-е изд.). ASA SIAM. ISBN 0-89871-425-7.
• Новак, MA (2006). Эволюционная динамика: исследование уравнений жизни . Издательство Гарвардского университета. ISBN 0-674-02338-2.
• Виртамо, Дж. "Процессы рождения-смерти" (PDF) . 38.3143 Теория очередей . Получено 2 декабря 2019 г. .