Проблема с ремнем
Проблема с ремнем

Задача о ремне — это математическая задача, которая требует нахождения длины скрещенного ремня , соединяющего два круглых шкива с радиусами r 1 и r 2, центры которых находятся на расстоянии P. Решение задачи о ремне требует тригонометрии и понятий двойной касательной , вертикального угла и конгруэнтных углов .

Решение

Очевидно, что треугольники ACO и ADO являются конгруэнтными прямоугольными треугольниками , как и треугольники BEO и BFO. Кроме того, треугольники ACO и BEO подобны . Поэтому углы CAO, DAO, EBO и FBO все равны. Обозначая этот угол через (выраженный в радианах ), длина ремня равна φ {\displaystyle \varphi}

С О + Д О + Э О + Ф О + дуга С Д + дуга Э Ф {\displaystyle CO+DO+EO+FO+{\text{arc}}CD+{\text{arc}}EF\,\!}
= 2 г 1 загар ⁡ ( φ ) + 2 г 2 загар ⁡ ( φ ) + ( 2 π − 2 φ ) г 1 + ( 2 π − 2 φ ) г 2 {\displaystyle =2r_{1}\tan(\varphi)+2r_{2}\tan(\varphi)+(2\pi -2\varphi)r_{1}+(2\pi -2\varphi)r_ {2}\,\!}
= 2 ( г 1 + г 2 ) ( загар ⁡ ( φ ) + π − φ ) {\displaystyle =2(r_{1}+r_{2})(\tan(\varphi)+\pi -\varphi)\,\!}

При этом используется удобство обозначения углов в радианах, поскольку длина дуги = радиус × величина угла , обращенного к дуге .

Чтобы найти, мы видим из подобия треугольников ACO и BEO, что φ {\displaystyle \varphi}

А О Б О = А С Б Э {\displaystyle {\frac {AO}{BO}}={\frac {AC}{BE}}\,\!}
⇒ П − х х = г 1 г 2 {\displaystyle \Стрелка вправо {\frac {Px}{x}}={\frac {r_{1}}{r_{2}}}\,\!}
⇒ П х = г 1 + г 2 г 2 {\displaystyle \Стрелка вправо {\frac {P}{x}}={\frac {r_{1}+r_{2}}{r_{2}}}\,\!}
⇒ х = П г 2 г 1 + г 2 {\displaystyle \Стрелка вправо {x}={\frac {Pr_{2}}{r_{1}+r_{2}}}\,\!}


потому что ⁡ ( φ ) = г 2 х = г 2 ( П г 2 г 1 + г 2 ) = г 1 + г 2 П {\displaystyle \cos(\varphi )={\frac {r_{2}}{x}}={\frac {r_{2}}{\left({\dfrac {Pr_{2}}{r_{1}+r_{2}}}\right)}}={\frac {r_{1}+r_{2}}{P}}\,\!}
⇒ φ = арккос ⁡ ( г 1 + г 2 П ) {\displaystyle \Rightarrow \varphi =\arccos \left({\frac {r_{1}+r_{2}}{P}}\right)\,\!}

При фиксированном P длина ремня зависит только от суммы значений радиуса r 1  +  r 2 , а не от их индивидуальных значений.

Проблема со шкивом

Проблема шкива

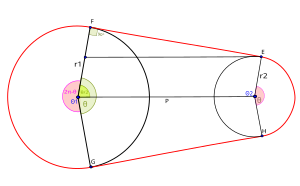
Существуют и другие типы задач, похожие на задачу с ремнем. Задача со шкивом , как показано, похожа на задачу с ремнем; однако ремень не пересекает сам себя. В задаче со шкивом длина ремня равна

2 П грех ⁡ ( θ 2 ) + г 1 ( 2 π − θ ) + г 2 θ , {\displaystyle 2P\sin \left({\frac {\theta }{2}}\right)+r_{1}(2\pi -\theta )+r_{2}{\theta }\,,}

где r 1 представляет собой радиус большего шкива, r 2 представляет собой радиус меньшего шкива, и:

θ = 2 арккос ⁡ ( г 1 − г 2 П ) . {\displaystyle \theta =2\arccos \left({\frac {r_{1}-r_{2}}{P}}\right)\,.}

Приложения

Проблема ремней используется [1] при проектировании самолетов , велосипедных передач , автомобилей и других предметов со шкивами или ремнями , которые пересекаются друг с другом. Проблема шкивов также используется при проектировании конвейерных лент, используемых в багажных лентах аэропортов и автоматизированных заводских линиях. [2]

Смотрите также

Ссылки

  1. ↑ Примеры тригонометрии в реальной жизни. Архивировано 25 апреля 2009 г. на Wayback Machine.
  2. ^ Тригонометрия, используемая в конвейерных лентах. Архивировано 22 февраля 2012 г. на Wayback Machine.
Взято с "https://en.wikipedia.org/w/index.php?title=Проблема_с_ремнем&oldid=1139729630"