Обратное снятие
Метод геофизического анализа

Back-stripping (также back stripping или backstripping) — это геофизический метод анализа, используемый для последовательностей осадочных пород . Он используется для количественной оценки глубины, на которой будет находиться фундамент при отсутствии осадочной и водной нагрузки. Эта глубина обеспечивает меру неизвестных тектонических движущих сил, которые ответственны за образование бассейна (иначе называемое тектоническим опусканием или подъемом). Сравнивая кривые backstripping с теоретическими кривыми опускания и подъема бассейна, можно вывести информацию о механизмах формирования бассейна. [1]

Методика, разработанная Уоттсом и Райаном в 1976 году [2], позволяет восстановить историю оседания и подъема фундамента при отсутствии осадочной и водной нагрузки и, следовательно, изолировать вклад тектонических сил, ответственных за образование рифтовой впадины. [3] Это метод, с помощью которого последовательные слои осадка, заполняющего впадину , «снимаются» с общей стратиграфии во время анализа истории этой впадины. В типичном сценарии осадочный бассейн углубляется от краевого изгиба , а сопровождающие его изохронные слои обычно утолщаются по направлению к впадине. Изолируя изохронные пакеты один за другим, их можно «снять» или отслоить назад — и нижнюю ограничивающую поверхность повернуть вверх к точке отсчета. Последовательно отслоив назад изохроны, можно построить историю углубления впадины в обратном порядке, что приводит к подсказкам относительно ее тектонического или изостатического происхождения. Более полный анализ использует декомпактизацию оставшейся последовательности после каждого этапа обратного обнажения. Это учитывает объем уплотнения, вызванного нагрузкой более поздних слоев, и позволяет лучше оценить толщину осадконакопления оставшихся слоев и изменение глубины воды со временем.

Общая теория

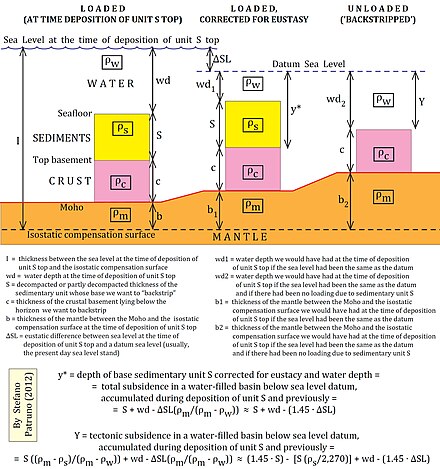
Схематическая диаграмма метода обратного снятия, относящаяся к уравнению ( 2 ). Нагруженная колонна относится к уравнению ( 3 ), а незагруженная колонна к уравнениям ( 4 ) и ( 5 )

В результате своей пористости осадочные слои уплотняются путем наложения осадочных слоев после осаждения. Следовательно, толщина каждого слоя в осадочной последовательности была больше во время его осаждения, чем при измерении в полевых условиях. Чтобы учесть влияние уплотнения осадков на толщину и плотность стратиграфической колонки, необходимо знать пористость. [4] [5] Эмпирические исследования показывают, что пористость горных пород уменьшается экспоненциально с глубиной. В общем, мы можем описать это с помощью соотношения:

ϕ = ϕ 0 е − с з {\displaystyle \phi =\phi _{0}e^{-cz}} ( 1 )


где — пористость породы на глубине , — пористость на поверхности, — удельная константа уплотнения породы. ϕ {\displaystyle \фи} з {\displaystyle z} ϕ 0 {\displaystyle \фи _{0}} с {\displaystyle с}

Уравнение обратного отрыва

Основное уравнение обратного зачистки корректирует наблюдаемые стратиграфические данные с учетом влияния осадочной и водной нагрузки, а также изменений глубины воды и имеет вид:

И = С ⋅ ( ρ м − ρ с ) ( ρ м − ρ ж ) + Вт г − Δ С Л ⋅ ρ м ( ρ м − ρ ж ) {\displaystyle Y=S\cdot {\frac {(\rho _{m}-\rho _{s})}{(\rho _{m}-\rho _{w})}}+W_{d}-\Delta _{SL}\cdot {\frac {\rho _{m}}{(\rho _{m}-\rho _{w})}}} ( 2 )


где - тектонически вызванное оседание, - толщина разуплотненного осадка, - средняя плотность осадка, - средняя глубина, на которой осадочные единицы были отложены, и - плотности воды и мантии соответственно, и разница в высоте уровня моря между настоящим и временем, когда осадки были отложены. Три независимых члена учитывают вклады нагрузки осадка, глубины воды и колебаний уровня моря в оседание бассейна. [1] [3] И {\displaystyle Y} С {\displaystyle S} ρ с {\displaystyle \rho _{s}} Вт г {\displaystyle W_{d}} ρ ж {\displaystyle \rho _{w}} ρ м {\displaystyle \rho _{м}} Δ С Л {\displaystyle \Дельта _{SL}}

Вывод

Чтобы вывести уравнение ( 2 ), следует сначала рассмотреть «нагруженную» колонну, которая представляет собой осадочную единицу, накопленную в течение определенного геологического периода времени, и соответствующую «ненагруженную» колонну, которая представляет собой положение нижележащего фундамента без влияния осадков. В сценарии давление у основания нагруженной колонны определяется как:

Вт г ρ ж г + С ρ с г + с ρ с г {\displaystyle W_{d}\rho _{w}г+S\rho _{s}г+c\rho _{c}г} ( 3 )

где - глубина воды осаждения, - средняя толщина корки, - толщина осадка, скорректированная на уплотнение, - средняя сила тяжести и , и - плотности воды, осадка и корки соответственно. Давление в основании незагруженной колонны определяется по формуле: Вт г {\displaystyle W_{d}} с {\displaystyle с} С {\displaystyle S} г {\displaystyle г} ρ ж {\displaystyle \rho _{w}} ρ с {\displaystyle \rho _{s}} ρ с {\displaystyle \rho _{c}}

И ρ ж г + с ρ с г + б ρ м г {\displaystyle Y\rho _{w}g+c\rho _{c}g+b\rho _{m}g} ( 4 )

где — тектоническое или скорректированное опускание, — плотность мантии, — расстояние от основания ненагруженной коры до глубины компенсации (которая, как предполагается, находится у основания нагруженной коры) и определяется по формуле: И {\displaystyle Y} ρ м {\displaystyle \rho _{м}} б {\displaystyle б}

б = С + Вт г − Δ С Л − И {\displaystyle b=S+W_{d}-\Delta _{SL}-Y} ( 5 )

Подставляя ( 3 ), ( 4 ) и ( 5 ) после упрощения получаем ( 2 ).

Многослойный чехол

Для многослойного осадочного бассейна необходимо последовательно откатывать каждый индивидуально идентифицируемый слой отдельно, чтобы получить полную эволюцию тектонического оседания. Используя уравнение ( 2 ), полный анализ оседания выполняется путем пошагового удаления верхнего слоя на любой одной стадии во время анализа и выполнения отката, как для случая одного слоя. Для оставшейся колонны средние плотности и толщина должны использоваться на каждом этапе времени или шаге расчета. [4] Уравнение ( 2 ) затем становится тектонической величиной оседания во время осадконакопления только самого верхнего слоя. В этом случае и может быть определено как толщина и плотность всей оставшейся осадочной колонны после удаления верхнего слоя (т. е. разуплотненная толщина). Толщина осадочной кучи со слоями тогда равна: Л ∗ {\displaystyle Л^{*}} ρ Л {\displaystyle \rho _{L}} л {\displaystyle л} л {\displaystyle л}

Л ∗ = ∑ дж = 1 л Л дж {\displaystyle L^{*}=\sum _{j=1}^{l}L_{j}} ( 6 )


Плотность осадочной колонны под слоем определяется средней плотностью всех оставшихся слоев. Это сумма всех плотностей оставшихся слоев, умноженная на соответствующую толщину и деленная на : л {\displaystyle л} Л ∗ {\displaystyle Л^{*}}

ρ Л ∗ = ∑ дж = 1 л Л дж ( ϕ дж ρ ж + ( 1 − ϕ дж ) ρ г ) Л ∗ {\displaystyle \rho _{L^{*}}={\frac {\sum _{j=1}^{l}L_{j}(\phi _{j}\rho _{w}+(1-\phi _{j})\rho _{g})}{L^{*}}}} ( 7 )


Фактически вы итеративно применяете ( 1 ) и ( 2 ), используя and вместо and . Л ∗ {\displaystyle Л^{*}} ρ Л ∗ {\displaystyle \rho _{L^{*}}} Л {\displaystyle L} ρ Л {\displaystyle \rho _{L}}

Ссылки

  1. ^ ab University of Wyoming: Backstripping Архивировано 15 декабря 2011 г. на Wayback Machine
  2. ^ Уоттс, AB; Райан, WBF (1976). «Прогиб литосферы и континентальные окраинные бассейны». Тектонофизика . 36 (1–3): 25–44. Bibcode : 1976Tectp..36...25W. doi : 10.1016/0040-1951(76)90004-4.
  3. ^ ab Глава 4: Анализ отката скважин и проседания [ постоянная мертвая ссылка ] в Гравитационные аномалии, прогиб и термомеханическая эволюция Западной Иберийской окраины и сопряженного с ней Ньюфаундленда (2008), докторская диссертация Тиаго Куньи
  4. ^ ab Геодинамика литосферы (2-е изд.), K. Stüwe (2007), Нью-Йорк: Springer]
  5. ^ Ли, EY, Новотны, Дж., Вагрейх, М. (2019) Анализ и визуализация проседания: для анализа и моделирования осадочного бассейна, Springer. doi : 10.1007/978-3-319-76424-5
Взято с "https://en.wikipedia.org/w/index.php?title=Back-stripping&oldid=1149744337"