Криптография с открытым ключом
Эта статья нуждается в дополнительных цитатах для проверки . ( январь 2024 г. ) |

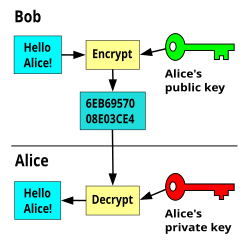

Криптография с открытым ключом , или асимметричная криптография , — это область криптографических систем , использующих пары связанных ключей. Каждая пара ключей состоит из открытого ключа и соответствующего ему закрытого ключа . [1] [2] Пары ключей генерируются с помощью криптографических алгоритмов, основанных на математических задачах, называемых односторонними функциями . Безопасность криптографии с открытым ключом зависит от сохранения секретного ключа; открытый ключ может быть распространен открыто без ущерба для безопасности. [3]
В системе шифрования с открытым ключом любой человек, имеющий открытый ключ, может зашифровать сообщение, получив зашифрованный текст , но только тот, кто знает соответствующий закрытый ключ, может расшифровать зашифрованный текст, чтобы получить исходное сообщение. [4]
Например, журналист может опубликовать открытый ключ пары ключей шифрования на веб-сайте, чтобы источники могли отправлять секретные сообщения новостной организации в виде зашифрованного текста. Только журналист, который знает соответствующий закрытый ключ, может расшифровать зашифрованные тексты, чтобы получить сообщения источников — подслушивающее устройство, читающее электронное письмо по пути к журналисту, не сможет расшифровать зашифрованные тексты.
В системе цифровой подписи отправитель может использовать закрытый ключ вместе с сообщением для создания подписи . Любой, у кого есть соответствующий открытый ключ, может проверить, соответствует ли подпись сообщению, но фальсификатор, не знающий закрытый ключ, не сможет найти ни одной пары сообщение/подпись, которая пройдет проверку с открытым ключом. [5] [6]
Например, издатель программного обеспечения может создать пару ключей подписи и включить открытый ключ в программное обеспечение, установленное на компьютерах. Позже издатель может распространить обновление программного обеспечения, подписанное с использованием закрытого ключа, и любой компьютер, получающий обновление, может подтвердить его подлинность, проверив подпись с использованием открытого ключа. Пока издатель программного обеспечения хранит закрытый ключ в секрете, даже если фальсификатор может распространить вредоносные обновления на компьютеры, он не сможет убедить компьютеры в том, что любые вредоносные обновления являются подлинными.
Алгоритмы открытого ключа являются фундаментальными примитивами безопасности в современных криптосистемах , включая приложения и протоколы, которые обеспечивают гарантию конфиденциальности, подлинности и неотказуемости электронных коммуникаций и хранения данных. Они лежат в основе многочисленных стандартов Интернета, таких как Transport Layer Security (TLS) , SSH , S/MIME и PGP . Некоторые алгоритмы открытого ключа обеспечивают распределение ключей и секретность (например, обмен ключами Диффи–Хеллмана ), некоторые обеспечивают цифровые подписи (например, алгоритм цифровой подписи ), а некоторые обеспечивают и то, и другое (например, RSA ). По сравнению с симметричным шифрованием , асимметричное шифрование может быть слишком медленным для многих целей. [7] Современные криптосистемы (такие как TLS , Secure Shell ) используют как симметричное шифрование, так и асимметричное шифрование, часто используя асимметричное шифрование для безопасного обмена секретным ключом, который затем используется для симметричного шифрования.
Описание
До середины 1970-х годов все системы шифрования использовали алгоритмы симметричного ключа , в которых один и тот же криптографический ключ используется с базовым алгоритмом как отправителем, так и получателем, которые оба должны хранить его в секрете. По необходимости, ключ в каждой такой системе должен был быть передан между общающимися сторонами каким-либо безопасным способом до любого использования системы, например, через безопасный канал . Это требование никогда не бывает тривиальным и очень быстро становится неуправляемым по мере увеличения числа участников, или когда безопасные каналы недоступны, или когда (как разумная криптографическая практика) ключи часто меняются. В частности, если сообщения должны быть защищены от других пользователей, для каждой возможной пары пользователей требуется отдельный ключ.
Напротив, в системе с открытым ключом открытые ключи могут распространяться широко и открыто, и только соответствующие им закрытые ключи должны храниться в секрете их владельцем.
Два наиболее известных применения криптографии с открытым ключом:
- Шифрование с открытым ключом, при котором сообщение шифруется открытым ключом предполагаемого получателя. Для правильно выбранных и используемых алгоритмов сообщения на практике не могут быть расшифрованы кем-либо, кто не обладает соответствующим закрытым ключом, который, таким образом, предполагается владельцем этого ключа и, следовательно, лицом, связанным с открытым ключом. Это может быть использовано для обеспечения конфиденциальности сообщения. [8]
- Цифровые подписи , в которых сообщение подписано закрытым ключом отправителя и может быть проверено любым, у кого есть доступ к открытому ключу отправителя. [9] Эта проверка доказывает, что отправитель имел доступ к закрытому ключу, и поэтому с большой вероятностью является лицом, связанным с открытым ключом. Она также доказывает, что подпись была подготовлена для этого конкретного сообщения, поскольку подпись, которая проходит проверку открытым ключом в одном сообщении, не пройдет проверку открытым ключом в других сообщениях.
Одним из важных вопросов является уверенность/доказательство того, что конкретный открытый ключ является подлинным, т. е. что он правильный и принадлежит заявленному лицу или организации, и не был подделан или заменен какой-либо (возможно, злонамеренной) третьей стороной. Существует несколько возможных подходов, включая:
Инфраструктура открытых ключей (PKI), в которой одна или несколько третьих сторон, известных как центры сертификации , удостоверяют право собственности на пары ключей. TLS опирается на это. Это подразумевает, что система PKI (программное обеспечение, оборудование и управление) заслуживает доверия всех участников.
« Сеть доверия » децентрализует аутентификацию, используя индивидуальные подтверждения связей между пользователем и открытым ключом, принадлежащим этому пользователю. PGP использует этот подход в дополнение к поиску в системе доменных имен (DNS). Система DKIM для цифровой подписи электронных писем также использует этот подход.
Приложения
Наиболее очевидным применением системы шифрования с открытым ключом является шифрование сообщений с целью обеспечения конфиденциальности — сообщение, которое отправитель шифрует с помощью открытого ключа получателя, может быть расшифровано только с помощью парного закрытого ключа получателя.
Другим применением криптографии с открытым ключом является цифровая подпись . Схемы цифровой подписи могут использоваться для аутентификации отправителя .
Системы неотказуемости используют цифровые подписи для того, чтобы гарантировать, что ни одна из сторон не сможет успешно оспорить свое авторство документа или сообщения.
Дополнительные приложения, созданные на этой основе, включают: цифровые деньги , соглашение о ключах с аутентификацией по паролю , службы отметки времени и протоколы неотказуемости.
Гибридные криптосистемы
Поскольку алгоритмы асимметричного ключа почти всегда намного более вычислительно интенсивны, чем симметричные, обычно используют алгоритм обмена асимметричными ключами открытый/закрытый для шифрования и обмена симметричным ключом , который затем используется криптографией с симметричным ключом для передачи данных с использованием теперь общего симметричного ключа для алгоритма шифрования с симметричным ключом. PGP , SSH и семейство схем SSL/TLS используют эту процедуру; поэтому они называются гибридными криптосистемами . Первоначальный обмен ключами на основе асимметричной криптографии для совместного использования сгенерированного сервером симметричного ключа от сервера к клиенту имеет преимущество в том, что не требует предварительного совместного использования симметричного ключа вручную, например, на печатной бумаге или дисках, перевозимых курьером, при этом обеспечивая более высокую пропускную способность данных криптографии с симметричным ключом по сравнению с криптографией с асимметричным ключом для оставшейся части общего соединения.
Слабые стороны
Как и во всех системах, связанных с безопасностью, в криптографии с открытым ключом есть различные потенциальные слабости. Помимо плохого выбора алгоритма асимметричного ключа (есть несколько алгоритмов, которые широко считаются удовлетворительными) или слишком короткой длины ключа, главный риск безопасности заключается в том, что закрытый ключ пары становится известным. Вся безопасность сообщений, аутентификации и т. д. тогда будет потеряна.
Кроме того, с появлением квантовых вычислений многие алгоритмы асимметричного ключа считаются уязвимыми для атак, и разрабатываются новые квантово-устойчивые схемы для преодоления этой проблемы. [10] [11]
Алгоритмы
Все схемы с открытым ключом теоретически подвержены « атаке поиска ключа методом перебора ». [12] Однако такая атака непрактична, если объем вычислений, необходимых для успеха — названный Клодом Шенноном «фактором работы» — находится вне досягаемости всех потенциальных злоумышленников. Во многих случаях фактор работы можно увеличить, просто выбрав более длинный ключ. Но другие алгоритмы могут изначально иметь гораздо более низкие факторы работы, что делает устойчивость к атаке методом перебора (например, с использованием более длинных ключей) несущественной. Были разработаны некоторые специальные и специфические алгоритмы для помощи в атаке на некоторые алгоритмы шифрования с открытым ключом; как шифрование RSA , так и шифрование ElGamal имеют известные атаки, которые намного быстрее, чем подход методом перебора. [ необходима цитата ] Однако ни один из них не достаточно улучшен, чтобы быть фактически практичным.
Были обнаружены основные уязвимости для нескольких ранее многообещающих алгоритмов асимметричного ключа. Алгоритм «упаковки рюкзака» оказался небезопасным после разработки новой атаки. [13] Как и все криптографические функции, реализации с открытым ключом могут быть уязвимы для атак по сторонним каналам , которые используют утечку информации для упрощения поиска секретного ключа. Они часто не зависят от используемого алгоритма. Ведутся исследования как для обнаружения, так и для защиты от новых атак.
Изменение открытых ключей
Еще одной потенциальной уязвимостью безопасности при использовании асимметричных ключей является возможность атаки «человек посередине» , при которой связь открытых ключей перехватывается третьей стороной («человек посередине»), а затем модифицируется для предоставления других открытых ключей. Зашифрованные сообщения и ответы должны, во всех случаях, перехватываться, расшифровываться и повторно шифроваться злоумышленником с использованием правильных открытых ключей для различных сегментов связи, чтобы избежать подозрений. [ необходима цитата ]
Связь считается небезопасной, когда данные передаются способом, допускающим перехват (также называемым « сниффинг »). Эти термины относятся к чтению личных данных отправителя в полном объеме. Связь особенно небезопасна, когда перехваты не могут быть предотвращены или отслежены отправителем. [14]
Атака «человек посередине» может быть труднореализуемой из-за сложности современных протоколов безопасности. Однако задача упрощается, когда отправитель использует небезопасные носители, такие как публичные сети, Интернет или беспроводную связь. В этих случаях злоумышленник может поставить под угрозу инфраструктуру связи, а не сами данные. Гипотетический злонамеренный сотрудник поставщика интернет-услуг (ISP) может посчитать атаку «человек посередине» относительно простой. Для захвата открытого ключа потребуется только поиск ключа, когда он отправляется через коммуникационное оборудование ISP; в правильно реализованных схемах асимметричного ключа это не представляет существенного риска. [ необходима цитата ]
В некоторых продвинутых атаках типа «человек посередине» одна сторона коммуникации увидит исходные данные, а другая получит вредоносный вариант. Асимметричные атаки типа «человек посередине» могут помешать пользователям осознать, что их соединение скомпрометировано. Это остается так даже тогда, когда известно, что данные одного пользователя скомпрометированы, потому что данные кажутся другому пользователю в порядке. Это может привести к запутанным разногласиям между пользователями, таким как «это должно быть на вашей стороне!», когда ни один из пользователей не виноват. Следовательно, атаки типа «человек посередине» полностью предотвратимы только тогда, когда инфраструктура связи физически контролируется одной или обеими сторонами; например, через проводной маршрут внутри собственного здания отправителя. Подводя итог, можно сказать, что открытые ключи легче изменить, когда коммуникационное оборудование, используемое отправителем, контролируется злоумышленником. [15] [16] [17]
Инфраструктура открытого ключа
Один из подходов к предотвращению таких атак предполагает использование инфраструктуры открытого ключа (PKI); набора ролей, политик и процедур, необходимых для создания, управления, распространения, использования, хранения и отзыва цифровых сертификатов и управления шифрованием с открытым ключом. Однако это имеет потенциальные недостатки.
Например, центр сертификации, выдающий сертификат, должен быть доверенным всеми участвующими сторонами, чтобы должным образом проверить личность держателя ключа, обеспечить правильность открытого ключа при выдаче сертификата, быть защищенным от компьютерного пиратства и договориться со всеми участниками о проверке всех их сертификатов до начала защищенных коммуникаций. Например, веб-браузеры поставляются с длинным списком «самоподписанных сертификатов идентификации» от поставщиков PKI — они используются для проверки добросовестности центра сертификации, а затем, на втором этапе, сертификатов потенциальных коммуникаторов. Злоумышленник, который может подделать один из этих центров сертификации, выдав сертификат для поддельного открытого ключа, может затем организовать атаку «человек посередине» так же легко, как если бы схема сертификатов вообще не использовалась. Злоумышленник, проникший на серверы органа власти и получивший доступ к его хранилищу сертификатов и ключей (открытых и закрытых), сможет подделывать, маскировать, расшифровывать и подделывать транзакции без ограничений, если ему удастся включиться в поток коммуникаций.
Несмотря на свои теоретические и потенциальные проблемы, инфраструктура открытого ключа широко используется. Примерами служат TLS и его предшественник SSL , которые обычно используются для обеспечения безопасности транзакций веб-браузера (например, большинство веб-сайтов используют TLS для HTTPS ).
Помимо устойчивости к атакам конкретной пары ключей, при развертывании систем открытых ключей необходимо учитывать безопасность иерархии сертификации . Некоторые центры сертификации — обычно специально созданная программа, работающая на сервере — ручаются за идентификаторы, назначенные определенным закрытым ключам, создавая цифровой сертификат. Цифровые сертификаты открытых ключей обычно действительны в течение нескольких лет, поэтому связанные с ними закрытые ключи должны надежно храниться в течение этого времени. Когда закрытый ключ, используемый для создания сертификата выше в иерархии сервера PKI, скомпрометирован или случайно раскрыт, возможна « атака посредника », что делает любой подчиненный сертификат полностью небезопасным.
Незашифрованные метаданные
Большинство доступных программ шифрования с открытым ключом не скрывают метаданные в заголовке сообщения, которые могут включать в себя идентификационные данные отправителя и получателя, дату отправки, поле темы, используемое ими программное обеспечение и т. д. Вместо этого скрывается только тело сообщения, которое может быть расшифровано только с помощью закрытого ключа предполагаемого получателя. Это означает, что третья сторона может построить довольно подробную модель участников сети связи вместе с обсуждаемыми темами, даже если само тело сообщения скрыто.
Однако недавно была продемонстрирована передача сообщений с зашифрованными заголовками, которая скрывает личности отправителя и получателя и значительно сокращает доступные метаданные для третьей стороны. [18] Концепция основана на открытом репозитории, содержащем отдельно зашифрованные блоки метаданных и зашифрованные сообщения. Только предполагаемый получатель может расшифровать блок метаданных, и сделав это, он может идентифицировать и загрузить свои сообщения и расшифровать их. Такая система обмена сообщениями в настоящее время находится в экспериментальной фазе и еще не развернута. Масштабирование этого метода раскроет третьей стороне только сервер входящих сообщений, используемый получателем, и временную метку отправки и получения. Сервер может совместно использоваться тысячами пользователей, что значительно усложнит моделирование социальных сетей.
История
В ранней истории криптографии две стороны полагались на ключ, которым они обменивались с помощью безопасного, но некриптографического метода, например, личной встречи или через доверенного курьера. Этот ключ, который обе стороны затем должны были хранить в абсолютной тайне, затем мог использоваться для обмена зашифрованными сообщениями. При таком подходе к распространению ключей возникает ряд существенных практических трудностей .
Ожидание
В своей книге 1874 года «Принципы науки» Уильям Стэнли Джевонс писал: [19]
Может ли читатель сказать, какие два числа, умноженные друг на друга, дадут число 8616460799 ? [20] Я думаю, что вряд ли кто-то, кроме меня, когда-либо узнает об этом. [19]
Здесь он описал связь односторонних функций с криптографией и продолжил обсуждение проблемы факторизации, используемой для создания функции-ловушки . В июле 1996 года математик Соломон В. Голомб сказал: «Джевонс предвидел ключевую особенность алгоритма RSA для криптографии с открытым ключом, хотя он, конечно, не изобрел концепцию криптографии с открытым ключом». [21]
Секретное открытие
В 1970 году Джеймс Х. Эллис , британский криптограф из Центра правительственной связи Великобритании (GCHQ), задумался о возможности «несекретного шифрования» (теперь называемого криптографией с открытым ключом), но не увидел способа реализовать его. [22] [23]
В 1973 году его коллега Клиффорд Кокс реализовал то, что стало известно как алгоритм шифрования RSA , предоставив практический метод «несекретного шифрования», а в 1974 году другой математик и криптограф GCHQ, Малкольм Дж. Уильямсон , разработал то, что сейчас известно как обмен ключами Диффи–Хеллмана . Схема была также передана Агентству национальной безопасности США . [24] Обе организации имели военную направленность, и в любом случае были доступны только ограниченные вычислительные мощности; потенциал криптографии с открытым ключом остался нереализованным ни одной из организаций:
Я посчитал, что это наиболее важно для военного использования... если вы можете быстро и в электронном виде поделиться своим ключом, у вас будет большое преимущество перед вашим противником. Только в конце эволюции от Бернерса-Ли, проектировавшего открытую интернет-архитектуру для ЦЕРНа , ее адаптации и принятия для Arpanet ... криптография с открытым ключом реализовала весь свой потенциал.
— Ральф Бенджамин [24]
Эти открытия не были публично признаны в течение 27 лет, пока исследование не было рассекречено британским правительством в 1997 году. [25]
Публичное открытие
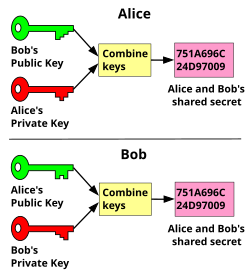
В 1976 году асимметричная ключевая криптосистема была опубликована Уитфилдом Диффи и Мартином Хеллманом , которые под влиянием работы Ральфа Меркла по распределению открытых ключей раскрыли метод соглашения об открытых ключах. Этот метод обмена ключами, который использует возведение в степень в конечном поле , стал известен как обмен ключами Диффи–Хеллмана . [26] Это был первый опубликованный практический метод установления общего секретного ключа по аутентифицированному (но не конфиденциальному) каналу связи без использования предварительного общего секрета. «Техника соглашения об открытых ключах» Меркла стала известна как « Головоломки Меркла » и была изобретена в 1974 году и опубликована только в 1978 году. Это делает асимметричное шифрование довольно новой областью в криптографии, хотя сама криптография насчитывает более 2000 лет. [27]
В 1977 году обобщение схемы Кокса было независимо изобретено Роном Ривестом , Ади Шамиром и Леонардом Адлеманом , которые тогда работали в Массачусетском технологическом институте . Последние авторы опубликовали свою работу в 1978 году в колонке Мартина Гарднера в Scientific American , и алгоритм стал известен как RSA , по их инициалам. [28] RSA использует возведение в степень по модулю произведения двух очень больших простых чисел для шифрования и дешифрования, выполняя как шифрование с открытым ключом, так и цифровые подписи с открытым ключом. Его безопасность связана с чрезвычайной сложностью факторизации больших целых чисел , проблемы, для которой не существует известной эффективной общей методики. Описание алгоритма было опубликовано в колонке Mathematical Games в выпуске Scientific American за август 1977 года . [29]
Начиная с 1970-х годов было разработано большое количество разнообразных методов шифрования, цифровой подписи, согласования ключей и других методов, включая криптосистему Рабина , шифрование Эль-Гамаля , DSA и ECC .
Примеры
Примеры хорошо зарекомендовавших себя методов асимметричного ключа для различных целей включают в себя:
- Протокол обмена ключами Диффи-Хеллмана
- DSS (стандарт цифровой подписи), включающий алгоритм цифровой подписи
- Эль-Гамаль
- Криптография на основе эллиптических кривых
- Алгоритм цифровой подписи на основе эллиптических кривых (ECDSA)
- Эллиптическая кривая Диффи-Хеллмана (ECDH)
- Ed25519 и Ed448 ( EdDSA )
- X25519 и X448 (ECDH/EdDH)
- Различные методы согласования ключей с аутентификацией по паролю
- Криптосистема Пайе
- Алгоритм шифрования RSA ( PKCS#1 )
- Криптосистема Крамера–Шоупа
- Протокол согласования аутентифицированных ключей YAK
Примеры алгоритмов асимметричного ключа, которые еще не получили широкого распространения, включают:
- Криптосистема NTRUEncrypt
- Кибер
- криптосистема Мак-Элиса
Примеры известных, но небезопасных алгоритмов асимметричного ключа включают в себя:
Примеры протоколов, использующих алгоритмы асимметричного ключа:
- S/MIME
- GPG , реализация OpenPGP и стандарт Интернета
- EMV , Центр сертификации EMV
- IPsec
- ПГП
- ZRTP , безопасный протокол VoIP
- Протокол Transport Layer Security, стандартизированный IETF и его предшественником Secure Socket Layer
- СИЛК
- SSH
- Биткойн
- Неофициальные сообщения
Смотрите также
- Книги по криптографии
- Защита конфиденциальности GNU
- Шифрование на основе идентификации (IBE)
- Депонирование ключей
- Протокол согласования ключей
- Список слов PGP
- Постквантовая криптография
- Довольно хорошая конфиденциальность
- Псевдоним
- Отпечаток открытого ключа
- Инфраструктура открытых ключей (PKI)
- Квантовые вычисления
- Квантовая криптография
- Безопасная оболочка (SSH)
- Алгоритм с симметричным ключом
- Пороговая криптосистема
- Сеть доверия
Примечания
- ^ Р. Ширей (август 2007 г.). Глоссарий безопасности Интернета, версия 2. Сетевая рабочая группа. doi : 10.17487/RFC4949 . RFC 4949. Информационный.
- ^ Бернстайн, Дэниел Дж.; Ланге, Таня (14 сентября 2017 г.). «Постквантовая криптография». Nature . 549 (7671): 188–194. Bibcode :2017Natur.549..188B. doi :10.1038/nature23461. ISSN 0028-0836. PMID 28905891. S2CID 4446249.
- ^ Столлингс, Уильям (3 мая 1990 г.). Криптография и сетевая безопасность: принципы и практика. Prentice Hall. стр. 165. ISBN 9780138690175.
- ^ Менезес, Альфред Дж .; Ван Ооршот, Пол К .; Ванстоун, Скотт А. (октябрь 1996 г.). "8: Шифрование с открытым ключом". Справочник по прикладной криптографии (PDF) . CRC Press. стр. 283–319. ISBN 0-8493-8523-7. Получено 8 октября 2022 г. .
- ^ Менезес, Альфред Дж .; Ван Ооршот, Пол К .; Ванстоун, Скотт А. (октябрь 1996 г.). "8: Шифрование с открытым ключом". Справочник по прикладной криптографии (PDF) . CRC Press. стр. 425–488. ISBN 0-8493-8523-7. Получено 8 октября 2022 г. .
- ^ Бернстайн, Дэниел Дж. (1 мая 2008 г.). «Защита коммуникаций от подделки». Алгоритмическая теория чисел (PDF) . Том 44. Публикации MSRI. §5: Подписи с открытым ключом, стр. 543–545 . Получено 8 октября 2022 г.
- ^ Альварес, Рафаэль; Кабальеро-Хиль, Кандидо; Сантоха, Хуан; Самора, Антонио (27 июня 2017 г.). «Алгоритмы облегченного обмена ключами». Датчики . 17 (7): 1517. дои : 10.3390/s17071517 . ISSN 1424-8220. ПМК 5551094 . ПМИД 28654006.
- ^ "Асимметричное шифрование". IONOS Digitalguide . Получено 2 июня 2022 г.
- ^ Михир, Белларе; Голдвассер, Шафи. "Глава 10: Цифровые подписи" (PDF) . Конспект лекций по криптографии .
- ^ Эскрибано Паблос, Хосе Игнасио; Гонсалес Васко, Мария Исабель (апрель 2023 г.). «Безопасный постквантовый групповой обмен ключами: реализация решения на основе Kyber». ИЭПП Коммуникации . 17 (6): 758–773. дои : 10.1049/cmu2.12561. hdl : 10016/37141 . ISSN 1751-8628. S2CID 255650398.
- ^ Stohrer, Christian; Lugrin, Thomas (2023), Mulder, Valentin; Mermoud, Alain; Lenders, Vincent; Tellenbach, Bernhard (ред.), «Асимметричное шифрование», Trends in Data Protection and Encryption Technologies , Cham: Springer Nature Switzerland, стр. 11–14, doi : 10.1007/978-3-031-33386-6_3 , ISBN 978-3-031-33386-6
- ^ Paar, Christof; Pelzl, Jan; Preneel, Bart (2010). Понимание криптографии: учебник для студентов и практиков. Springer. ISBN 978-3-642-04100-6.
- ^ Шамир, Ади (ноябрь 1982 г.). «Алгоритм полиномиального времени для взлома базовой криптосистемы Меркла-Хеллмана». 23-й ежегодный симпозиум по основам компьютерной науки (SFCS 1982) : 145–152. doi :10.1109/SFCS.1982.5.
- ^ Tunggal, Abi (20 февраля 2020 г.). «Что такое атака «человек посередине» и как ее предотвратить — в чем разница между атакой «человек посередине» и сниффингом?». UpGuard . Получено 26 июня 2020 г.[ самостоятельно опубликованный источник? ]
- ^ Tunggal, Abi (20 февраля 2020 г.). «Что такое атака типа «человек посередине» и как ее предотвратить — где происходят атаки типа «человек посередине»?». UpGuard . Получено 26 июня 2020 г.[ самостоятельно опубликованный источник? ]
- ^ martin (30 января 2013 г.). «Китай, GitHub и человек посередине». GreatFire . Архивировано из оригинала 19 августа 2016 г. Получено 27 июня 2015 г.[ самостоятельно опубликованный источник? ]
- ^ percy (4 сентября 2014 г.). «Власти запускают атаку «человек посередине» на Google». GreatFire . Получено 26 июня 2020 г. .[ самостоятельно опубликованный источник? ]
- ^ Бьоргвинсдоттир, Ханна; Бентли, Фил (24 июня 2021 г.). «Warp2: метод электронной почты и обмена сообщениями с зашифрованной адресацией и заголовками». arXiv : 1411.6409 [cs.CR].
- ^ ab Jevons, WS (1874). Принципы науки: трактат о логике и научном методе. Macmillan & Co. стр. 141. Получено 18 января 2024 г.
- ^ Weisstein, EW (2024). «Число Джевонса». MathWorld . Получено 18 января 2024 г. .
- ^ Golob, Solomon W. (1996). «О факторизации числа Джевонса». Cryptologia . 20 (3): 243. doi :10.1080/0161-119691884933. S2CID 205488749.
- ^ Эллис, Джеймс Х. (январь 1970 г.). «Возможность безопасного несекретного цифрового шифрования» (PDF) . CryptoCellar . Получено 18 января 2024 г. .
- ^ Сойер, Патрик (11 марта 2016 г.). «Невоспетый гений, который обеспечил компьютерную защиту Великобритании и проложил путь к безопасным покупкам в Интернете». The Telegraph .
- ^ ab Эспинер, Том (26 октября 2010 г.). «Пионеры GCHQ о рождении криптографии с открытым ключом». ZDNet .
- ^ Сингх, Саймон (1999). Книга кодов . Doubleday. С. 279–292.
- ^ Диффи, Уитфилд ; Хеллман, Мартин Э. (ноябрь 1976 г.). «Новые направления в криптографии» (PDF) . Труды IEEE по теории информации . 22 (6): 644–654. CiteSeerX 10.1.1.37.9720 . doi :10.1109/TIT.1976.1055638. Архивировано (PDF) из оригинала 29 ноября 2014 г.
- ^ "Асимметричное шифрование". IONOS Digitalguide . Получено 9 июня 2022 г.
- ^ Rivest, R.; Shamir, A.; Adleman, L. (февраль 1978 г.). "Метод получения цифровых подписей и криптосистем с открытым ключом" (PDF) . Communications of the ACM . 21 (2): 120–126. CiteSeerX 10.1.1.607.2677 . doi :10.1145/359340.359342. S2CID 2873616. Архивировано из оригинала (PDF) 17 декабря 2008 г. . Получено 15 ноября 2019 г. .
- ^ Робинсон, Сара (июнь 2003 г.). «Все еще охраняя секреты после многих лет атак, RSA зарабатывает почести своим основателям» (PDF) . SIAM News . 36 (5).
Ссылки
- Хирш, Фредерик Дж. "SSL/TLS Strong Encryption: An Introduction". Apache HTTP Server . Получено 17 апреля 2013 г.. Первые два раздела содержат очень хорошее введение в криптографию с открытым ключом.
- Фергюсон, Нильс ; Шнайер, Брюс (2003). Практическая криптография . Wiley . ISBN 0-471-22357-3.
- Кац, Джон ; Линделл, Ю. (2007). Введение в современную криптографию. CRC Press . ISBN 978-1-58488-551-1.
- Менезес, А. Дж .; ван Ооршот, П. К.; Ванстоун, Скотт А. (1997). Справочник по прикладной криптографии. Тейлор и Фрэнсис. ISBN 0-8493-8523-7.
- IEEE 1363: Стандартные спецификации для криптографии с открытым ключом
- Кристоф Паар, Ян Пельцль, «Введение в криптографию с открытым ключом», Глава 6 книги «Понимание криптографии. Учебник для студентов и практиков». (сопутствующий веб-сайт содержит онлайн-курс по криптографии, охватывающий криптографию с открытым ключом), Springer, 2009.
- Саломаа, Арто (1996). Криптография с открытым ключом (2-е изд.). Берлин: Шпрингер . 275. дои : 10.1007/978-3-662-03269-5. ISBN 978-3-662-03269-5. S2CID 24751345.
Внешние ссылки
- Устное интервью с Мартином Хеллманом, Институт Чарльза Бэббиджа , Университет Миннесоты. Ведущий ученый-криптограф Мартин Хеллман обсуждает обстоятельства и фундаментальные идеи своего изобретения криптографии с открытым ключом с соавторами Уитфилдом Диффи и Ральфом Мерклем в Стэнфордском университете в середине 1970-х годов.
- Рассказ о том, как GCHQ хранил в секрете свое изобретение PKE до 1997 года
