Астросейсмология

Астросейсмология — это изучение колебаний в звездах. Звезды имеют множество резонансных мод и частот, а путь звуковых волн, проходящих через звезду, зависит от локальной скорости звука , которая, в свою очередь, зависит от локальной температуры и химического состава. Поскольку полученные моды колебаний чувствительны к различным частям звезды, они информируют астрономов о внутренней структуре звезды, что в противном случае невозможно напрямую определить из общих свойств, таких как яркость и температура поверхности.
Астросейсмология тесно связана с гелиосейсмологией , изучением звездной пульсации , в частности, на Солнце . Хотя обе они основаны на одной и той же базовой физике, для Солнца доступно больше качественно иной информации, поскольку его поверхность может быть разрешена.
Теоретическая основа

Линейно возмущая уравнения, определяющие механическое равновесие звезды (т. е. сохранение массы и гидростатическое равновесие ), и предполагая, что возмущения адиабатические, можно вывести систему из четырех дифференциальных уравнений , решения которой дают частоту и структуру мод колебаний звезды. Обычно предполагается, что структура звезды сферически симметрична, поэтому горизонтальная (т. е. нерадиальная) составляющая колебаний описывается сферическими гармониками , индексированными угловым градусом и азимутальным порядком . В невращающихся звездах моды с одинаковым угловым градусом должны иметь одинаковую частоту, поскольку нет предпочтительной оси. Угловой градус указывает количество узловых линий на поверхности звезды, поэтому при больших значениях противостоящие секторы примерно компенсируют друг друга, что затрудняет обнаружение изменений света. Как следствие, моды могут быть обнаружены только до углового градуса около 3 по интенсивности и около 4, если наблюдаются по лучевой скорости.
Дополнительно предполагая, что возмущение гравитационного потенциала пренебрежимо мало ( приближение Каулинга ) и что структура звезды меняется медленнее с радиусом, чем мода колебаний, уравнения можно приблизительно свести к одному уравнению второго порядка для радиальной составляющей собственной функции смещения , где — радиальная координата в звезде, — угловая частота моды колебаний, — скорость звука внутри звезды, — частота Брента–Вяйсяля или плавучести, а — частота Лэмба. Последние два определяются как и соответственно. По аналогии с поведением простых гармонических осцилляторов это означает, что осциллирующие решения существуют, когда частота либо больше, либо меньше, чем и . Мы идентифицируем первый случай как высокочастотные моды давления (p-моды), а второй — как низкочастотные гравитационные моды (g-моды).
Это базовое разделение позволяет нам определить (с разумной точностью), где мы ожидаем, что какой тип моды будет резонировать в звезде. Построив кривые и (для заданных ), мы ожидаем, что p-моды будут резонировать на частотах ниже обеих кривых или на частотах выше обеих кривых.
Механизмы возбуждения
Каппа-механизм
При довольно специфических условиях некоторые звезды имеют области, где тепло переносится излучением, а непрозрачность является резко убывающей функцией температуры. Этот выступ непрозрачности может приводить в движение колебания через -механизм (или клапан Эддингтона ). Предположим, что в начале цикла колебаний оболочка звезды сжимается. Расширяясь и слегка охлаждаясь, слой в выступе непрозрачности становится более непрозрачным, поглощает больше излучения и нагревается. Этот нагрев вызывает расширение, дальнейшее охлаждение, и слой становится еще более непрозрачным. Это продолжается до тех пор, пока непрозрачность материала не перестает увеличиваться так быстро, и в этот момент излучение, захваченное в слое, может вырваться. Звезда сжимается, и цикл готовится начаться снова. В этом смысле непрозрачность действует как клапан, который удерживает тепло в оболочке звезды.
Пульсации, вызванные -механизмом, когерентны и имеют относительно большие амплитуды. Он управляет пульсациями во многих из самых длинных известных переменных звезд, включая переменные цефеиды и RR Лиры .
Поверхностная конвекция
В звездах с поверхностными конвективными зонами турбулентные движения жидкостей вблизи поверхности одновременно возбуждают и гасят колебания в широком диапазоне частот. [2] [3] Поскольку моды по своей природе стабильны, они имеют низкие амплитуды и относительно недолговечны. Это движущий механизм во всех осцилляторах солнечного типа.
Конвективная блокировка
Если основание зоны поверхностной конвекции острое, а конвективные временные шкалы медленнее, чем пульсационные, конвективные потоки слишком медленно реагируют на возмущения, которые могут перерасти в большие, когерентные пульсации. Этот механизм известен как конвективная блокировка [4] и, как полагают, вызывает пульсации в переменных Doradus. [5]
Приливное возбуждение
Наблюдения со спутника «Кеплер» выявили эксцентричные двойные системы, в которых колебания возбуждаются во время максимального сближения. [6] Эти системы известны как звезды с сердцебиением из-за характерной формы кривых блеска.
Типы осцилляторов
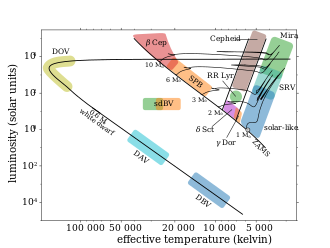
Генераторы солнечного типа
Поскольку солнечные колебания вызываются приповерхностной конвекцией, любые звездные колебания, вызванные аналогичным образом, известны как солнечноподобные колебания , а сами звезды как солнечноподобные осцилляторы . Однако солнечноподобные колебания также происходят в эволюционировавших звездах (субгигантах и красных гигантах), которые имеют конвективные оболочки, даже если звезды не являются солнцеподобными .
Переменные цефеиды
Переменные цефеиды являются одним из важнейших классов пульсирующих звезд. Это звезды с гелиевым ядром и массой более 5 солнечных масс. Они в основном колеблются в своих основных модах с типичными периодами от нескольких дней до нескольких месяцев. Их периоды пульсации тесно связаны с их светимостью, поэтому можно определить расстояние до цефеиды, измерив ее период колебаний, вычислив ее светимость и сравнив ее с наблюдаемой яркостью.
Пульсации цефеид возбуждаются каппа-механизмом, действующим на вторую зону ионизации гелия.
Переменные типа RR Лиры
RR Лиры похожи на переменные цефеиды, но имеют меньшую металличность (т. е. Популяция II ) и гораздо меньшую массу (примерно от 0,6 до 0,8 солнечной). Это гиганты, сжигающие гелий в ядре, которые колеблются в одной или обеих своих основных модах или первом обертоне. Колебания также обусловлены каппа-механизмом, действующим через вторую ионизацию гелия. Многие RR Лиры, включая саму RR Лиру, демонстрируют долгопериодные амплитудные модуляции, известные как эффект Блажко .
Звезды Дельта Щита и Гамма Дорадус
Переменные типа Дельта Щита находятся примерно там, где классическая полоса нестабильности пересекает главную последовательность. Обычно это карлики и субгиганты от A до ранних F-типов, а моды колебаний — это радиальные и нерадиальные моды давления низкого порядка с периодами от 0,25 до 8 часов и вариациями величины в любом месте между ними. [ необходимо разъяснение ] Как и переменные типа цефеид, колебания вызываются каппа-механизмом, действующим на вторичную ионизацию гелия.
Переменные типа SX Phoenicis считаются бедными металлами родственниками переменных типа Delta Scuti.
Переменные типа Гамма-Золотая Рыба встречаются в звездах, подобных красному концу переменных типа Дельта Щита, обычно раннего F-типа. Звезды показывают множественные частоты колебаний между 0,5 и 3 днями, что намного медленнее, чем низкопорядковые моды давления. Колебания типа Гамма-Золотая Рыба обычно считаются высокопорядковыми гравитационными модами, возбуждаемыми конвективной блокировкой.
Согласно результатам Кеплера , похоже, что многие звезды Дельта Щита также демонстрируют колебания Гамма Золотой Рыбы и, следовательно, являются гибридами. [7] [8]
Быстро колеблющиеся звезды Ap (roAp)
Быстро колеблющиеся Ap-звезды имеют параметры, схожие с параметрами переменных типа Дельта Щита, в основном это A- и F-типы, но они также сильно магнитные и химически пекулярные (отсюда спектральный подтип p ). Их плотные модовые спектры понимаются в терминах модели косого пульсатора : частоты мод модулируются магнитным полем, которое не обязательно совпадает с вращением звезды (как в случае с Землей). Моды колебаний имеют частоты около 1500 мкГц и амплитуды в несколько мм.
Медленно пульсирующие звезды B и переменные типа Бета Цефея
Медленно пульсирующие звезды B (SPB) — это звезды B-типа с периодами колебаний в несколько дней, которые считаются гравитационными модами высокого порядка, возбуждаемыми каппа-механизмом. Переменные типа Бета Цефея немного горячее (и, следовательно, массивнее), также имеют моды, возбуждаемые каппа-механизмом, и дополнительно колеблются в гравитационных модах низкого порядка с периодами в несколько часов. Оба класса осцилляторов содержат только медленно вращающиеся звезды.
Переменные субкарликовые звезды класса B
Звезды субкарликового класса B (sdB) по сути являются ядрами гигантов с гелиевым ядром, которые каким-то образом утратили большую часть своих водородных оболочек, в той степени, в которой нет оболочки, сжигающей водород. Они имеют множественные периоды колебаний, которые варьируются от 1 до 10 минут, и амплитуды где-то между 0,001 и 0,3 зв. величины в видимом свете. Колебания являются модами давления низкого порядка, возбуждаемыми каппа-механизмом, действующим на выпуклость непрозрачности железа.
Белые карлики
Белые карлики характеризуются спектральным типом, как и обычные звезды, за исключением того, что соотношение между спектральным типом и эффективной температурой не соответствует таким же образом. Таким образом, белые карлики известны как типы DO, DA и DB. Более холодные типы физически возможны, но Вселенная слишком молода, чтобы они достаточно остыли. Обнаружено, что белые карлики всех трех типов пульсируют. Пульсаторы известны как звезды GW Virginis (переменные DO, иногда также известные как звезды PG 1159), звезды V777 Herculis (переменные DB) и звезды ZZ Ceti (переменные DA). Все они пульсируют в g-модах низкой степени и высокого порядка. Периоды колебаний в целом уменьшаются с эффективной температурой, варьируясь от примерно 30 минут до примерно 1 минуты. Считается, что звезды GW Virginis и ZZ Ceti возбуждаются каппа-механизмом; звезды V777 Herculis — конвективным блокированием.
Космические миссии
Ряд прошлых, настоящих и будущих космических аппаратов включают астросейсмологические исследования в качестве значительной части своих миссий (в хронологическом порядке).
- WIRE – Спутник НАСА , запущенный в 1999 году. Неудачный большой инфракрасный телескоп, двухдюймовый апертурный звездный трекер использовался более десятилетия как инструмент астросейсмологии ярких звезд. Повторно вошел в атмосферу Земли в 2011 году.
- MOST – канадский спутник, запущенный в 2003 году. Первый космический аппарат, предназначенный для астросейсмологии.
- CoRoT – французский спутник ЕКА для поиска планет и астросейсмологии, запущенный в 2006 году.
- Космический телескоп «Кеплер» — космический аппарат НАСА для поиска планет, запущенный в 2009 году и переименованный в K2 , поскольку отказ второго маховика не позволил телескопу продолжить наблюдение за тем же полем.
- BRITE – Созвездие наноспутников, используемых для изучения самых ярких колеблющихся звезд. Первые два спутника запущены 25 февраля 2013 года.
- TESS – космический аппарат НАСА для поиска планет, который будет исследовать яркие звезды по всему небу, запущен в 2018 году.
- PLATO – планируемая миссия ЕКА , которая будет специально использовать астросейсмологию для получения точных масс и радиусов транзитных планет.
Смотрите также
- Разделение частот
- Звездотрясение
- Дискосейсмология – изучение колебательных режимов в аккреционных дисках.
- Сейсмология – научное изучение землетрясений и распространения упругих волн через планету.
- Телескоп Whole Earth – международное сотрудничество по наблюдению за переменными звездами
Ссылки
- ^ Кристенсен-Дальсгаард, Дж.; Даппен, В.; Аджуков, С.В. и (1996), «Современное состояние моделирования Солнца», Science , 272 (5266): 1286–1292, Bibcode : 1996Sci...272.1286C, doi : 10.1126/science.272.5266.1286, PMID 8662456, S2CID 35469049
- ^ Голдрайх, Питер ; Кили, Дуглас А. (февраль 1977 г.), «Солнечная сейсмология. II — Стохастическое возбуждение солнечных p-мод турбулентной конвекцией», The Astrophysical Journal , 212 : 243–251, Bibcode : 1977ApJ...212..243G, doi : 10.1086/155043
- ^ Кристенсен-Дальсгаард, Йорген ; Франдсен, Сорен (январь 1983 г.), «Звездные 5-минутные колебания», Solar Physics , 82 (1–2): 469–486, Bibcode : 1983SoPh...82..469C, doi : 10.1007/bf00145588, S2CID 125358311
- ^ Песнелл, У. Дин (март 1987 г.), «Новый механизм управления звездными пульсациями», The Astrophysical Journal , 314 : 598–604, Bibcode : 1987ApJ...314..598P, doi : 10.1086/165089
- ^ Гузик, Джойс А.; Кей, Энтони Б.; Брэдли, Пол А.; Кокс, Артур Н.; Нойфорж, Коринн (10 октября 2000 г.), «Управление пульсациями гравитационного режима в переменных γ Золотой Рыбы», The Astrophysical Journal Letters , 542 (1): L57–L60, Bibcode : 2000ApJ...542L..57G, doi : 10.1086/312908
- ^ Томпсон, С. Эверетт, М.; Маллалли, Ф.; Барклай, Т. и (2012), «Класс эксцентричных двойных звезд с динамическими приливными искажениями, обнаруженный с помощью Кеплера», The Astrophysical Journal , 753 (1): 86, arXiv : 1203.6115 , Bibcode : 2012ApJ...753...86T, doi : 10.1088/0004-637x/753/1/86, S2CID 119203028
- ^ Григачен, А.; Анточи, В.; Балона, Л.; Катандзаро, Г. и (2010), «Гибридные пульсаторы $\gamma$ Doradus-$\delta$ Scuti: новый взгляд на физику колебаний на основе наблюдений Кеплера», The Astrophysical Journal Letters , 713 (2): L192–L197 , arXiv : 1001.0747 , Bibcode : 2010ApJ...713L.192G, doi : 10.1088/2041-8205/713/2/L192, S2CID 56144432
- ^ Balona, LA (2014), «Низкие частоты в звездах типа $\delta$ Щита в системе Кеплера», Monthly Notices of the Royal Astronomical Society , 437 (2): 1476–1484, Bibcode : 2014MNRAS.437.1476B, doi : 10.1093/mnras/stt1981
Дальнейшее чтение
- Аэртс, Конни; Кристенсен-Дальсгаард, Йорген; Курц, Дональд (2010). Астеросейсмология . Библиотека астрономии и астрофизики. Дордрехт, Нью-Йорк: Springer. ISBN 978-1-4020-5803-5.
- Кристенсен-Дальсгаард, Йорген. «Конспект лекций по звёздным колебаниям» . Проверено 5 июня 2015 г.
- Пайперс, Фрэнк П. (2006). Методы в гелио- и астросейсмологии . Лондон: Imperial College Press. ISBN 978-1-8609-4755-1.
Программное обеспечение
Пакет Variable Star (на языке R) предоставляет основные функции для анализа закономерностей колебательных режимов переменных звезд. Также предоставляется пользовательский интерфейс для экспериментов с синтетическими данными.














