Уравнение Аррениуса
Формула температурной зависимости скоростей химических реакций

В физической химии уравнение Аррениуса представляет собой формулу для температурной зависимости скоростей реакций . Уравнение было предложено Сванте Аррениусом в 1889 году на основе работы голландского химика Якобуса Генрикуса ван 'т Хоффа , который в 1884 году заметил, что уравнение ван 'т Хоффа для температурной зависимости констант равновесия предполагает такую ​​формулу для скоростей как прямых, так и обратных реакций. Это уравнение имеет обширное и важное применение при определении скорости химических реакций и для расчета энергии активации . Аррениус дал физическое обоснование и интерпретацию формулы. [1] [2] [3] [4] В настоящее время ее лучше всего рассматривать как эмпирическую зависимость . [5] : 188  Ее можно использовать для моделирования температурного изменения коэффициентов диффузии , заселения кристаллических вакансий , скоростей ползучести и многих других термически индуцированных процессов и реакций. Уравнение Эйринга , разработанное в 1935 году, также выражает связь между скоростью и энергией.

Формулировка

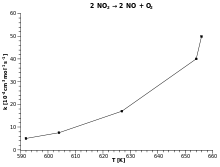
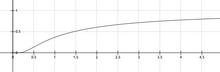
Почти во всех практических случаях k быстро увеличивается с ростом T. Э а ≫ Р Т {\displaystyle E_{a}\gg RT}
Математически, при очень высоких температурах, когда , k выравнивается и приближается к A как к пределу, но этот случай не встречается в практических условиях. Э а ≪ Р Т {\displaystyle E_{a}\ll RT}

Уравнение Аррениуса описывает экспоненциальную зависимость константы скорости химической реакции от абсолютной температуры следующим образом : где к = А е − Э а Р Т , {\displaystyle k=Ae^{\frac {-E_{\text{a}}}{RT}},}

Альтернативно, уравнение может быть выражено как где k = A e − E a k B T , {\displaystyle k=Ae^{\frac {-E_{\text{a}}}{k_{\text{B}}T}},}

Единственное отличие — это единица измерения E a : первая форма использует энергию на моль , что является общепринятым в химии, тогда как вторая форма использует энергию на молекулу напрямую, что является общепринятым в физике. Различные единицы учитываются при использовании либо газовой постоянной , R , либо постоянной Больцмана , k B , в качестве множителя температуры T .

Единица измерения предэкспоненциального множителя A идентична единице измерения константы скорости и будет меняться в зависимости от порядка реакции. Если реакция первого порядка, то она имеет единицу измерения с −1 , и по этой причине ее часто называют фактором частоты или частотой попыток реакции. Проще говоря, k — это число столкновений, которые приводят к реакции в секунду, A — это число столкновений (приводящих к реакции или нет) в секунду, происходящих с правильной ориентацией для реакции [7], и это вероятность того, что любое данное столкновение приведет к реакции. Можно видеть, что либо увеличение температуры, либо уменьшение энергии активации (например, за счет использования катализаторов ) приведет к увеличению скорости реакции. e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}

Учитывая небольшой температурный диапазон кинетических исследований, разумно аппроксимировать энергию активации как независимую от температуры. Аналогично, в широком диапазоне практических условий слабая температурная зависимость предэкспоненциального множителя пренебрежимо мала по сравнению с температурной зависимостью множителя ⁠ ⁠ e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}} ; за исключением случая «безбарьерных» диффузионно -ограниченных реакций, в которых предэкспоненциальный множитель является доминирующим и непосредственно наблюдаемым.

С помощью этого уравнения можно приблизительно оценить, что скорость реакции увеличивается примерно в 2–3 раза при повышении температуры на каждые 10 °C при обычных значениях энергии активации и температурного диапазона. [8]

Фактор обозначает долю молекул с энергией больше или равной . [9] e − E a R T {\displaystyle e^{\frac {-E_{a}}{RT}}} E a {\displaystyle E_{a}}

Вывод

Вант-Гофф утверждал, что температура реакции и стандартная константа равновесия имеют следующую связь: T {\displaystyle T} k e 0 {\displaystyle k_{\text{e}}^{0}}

где обозначает соответствующее стандартное значение изменения внутренней энергии . Δ U 0 {\displaystyle \Delta U^{0}}

Пусть и обозначают соответственно прямую и обратную скорости интересующей реакции, тогда ⁠ ⁠ , [10] уравнение из которого естественным образом следует. k f {\displaystyle k_{\text{f}}} k b {\displaystyle k_{\text{b}}} k e 0 = k f k b {\displaystyle k_{\text{e}}^{0}={\frac {k_{\text{f}}}{k_{\text{b}}}}} ln ⁡ k e 0 = ln ⁡ k f − ln ⁡ k b {\displaystyle \ln k_{\text{e}}^{0}=\ln k_{\text{f}}-\ln k_{\text{b}}}

Подставляя выражение в уравнение ( 1 ), получаем ⁠ ⁠ . ln ⁡ k e 0 {\displaystyle \ln k_{\text{e}}^{0}} d ln ⁡ k f d T − d ln ⁡ k b d T = Δ U 0 R T 2 {\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}-{\frac {d\ln k_{\text{b}}}{dT}}={\frac {\Delta U^{0}}{RT^{2}}}}

Предыдущее уравнение можно разбить на следующие два уравнения:

и

где и — энергии активации, связанные с прямой и обратной реакциями соответственно, при этом . E f {\displaystyle E_{\text{f}}} E b {\displaystyle E_{\text{b}}} Δ U 0 = E f − E b {\displaystyle \Delta U^{0}=E_{\text{f}}-E_{\text{b}}}

Экспериментальные данные показывают, что константы в ур. ( 2 ) и ур. ( 3 ) можно считать равными нулю, так что

и

Интегрирование этих уравнений и взятие экспоненты дает результаты ⁠ ⁠ k f = A f e − E f / R T {\displaystyle k_{\text{f}}=A_{\text{f}}e^{-E_{\text{f}}/RT}} и ⁠ ⁠ k b = A b e − E b / R T {\displaystyle k_{\text{b}}=A_{\text{b}}e^{-E_{\text{b}}/RT}} , где каждый предэкспоненциальный множитель или математически является экспонентой постоянной интегрирования для соответствующего неопределенного интеграла в вопросе. [11] A f {\displaystyle A_{\text{f}}} A b {\displaystyle A_{\text{b}}}

график Аррениуса

Линейный график Аррениуса: ln  k от 1/ T .

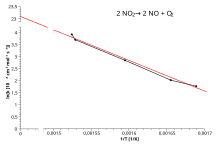
Натуральный логарифм уравнения Аррениуса дает: ln ⁡ k = ln ⁡ A − E a R 1 T . {\displaystyle \ln k=\ln A-{\frac {E_{\text{a}}}{R}}{\frac {1}{T}}.}

Перестановка дает: ln ⁡ k = − E a R ( 1 T ) + ln ⁡ A . {\displaystyle \ln k={\frac {-E_{\text{a}}}{R}}\left({\frac {1}{T}}\right)+\ln A.}

Это имеет ту же форму , что и уравнение прямой линии: где x — величина , обратная T. y = a x + b , {\displaystyle y=ax+b,}

Итак, когда реакция имеет константу скорости, подчиняющуюся уравнению Аррениуса, график зависимости ln  k от T −1 дает прямую линию, наклон и отсекаемый элемент которой можно использовать для определения E a и A соответственно. Эта процедура распространена в экспериментальной химической кинетике. Энергия активации просто получается путем умножения на (− R ) наклона прямой линии, проведенной из графика зависимости ln  k от (1/ T ): E a ≡ − R [ ∂ ln ⁡ k ∂ ( 1 / T ) ] P . {\displaystyle E_{\text{a}}\equiv -R\left[{\frac {\partial \ln k}{\partial (1/T)}}\right]_{P}.}

Модифицированное уравнение Аррениуса

Модифицированное уравнение Аррениуса [12] делает явной температурную зависимость предэкспоненциального множителя. Модифицированное уравнение обычно имеет вид k = A T n e − E a R T . {\displaystyle k=AT^{n}e^{\frac {-E_{\text{a}}}{RT}}.}

Исходное выражение Аррениуса выше соответствует n = 0. Подогнанных констант скорости обычно лежат в диапазоне −1 < n < 1. Теоретический анализ дает различные предсказания для n . Было отмечено, что «невозможно установить на основе температурных исследований константы скорости, наблюдается ли экспериментально предсказанная зависимость T 1/2 предэкспоненциального множителя». [5] : 190  Однако, если доступны дополнительные доказательства из теории и/или из эксперимента (например, зависимость от плотности), нет никаких препятствий для точных проверок закона Аррениуса.

Другой распространенной модификацией является растянутая экспоненциальная форма [ требуется ссылка ] , где β — безразмерное число порядка 1. Обычно это рассматривается как чисто эмпирическая поправка или фактор подгонки, позволяющий модели соответствовать данным, но может иметь и теоретическое значение, например, показывая наличие диапазона энергий активации или в особых случаях, таких как скачок диапазона переменной Мотта . k = A exp ⁡ [ − ( E a R T ) β ] , {\displaystyle k=A\exp \left[-\left({\frac {E_{a}}{RT}}\right)^{\beta }\right],}

Теоретическая интерпретация

Концепция энергии активации Аррениуса

Аррениус утверждал, что для того, чтобы реагенты превратились в продукты, они должны сначала приобрести минимальное количество энергии, называемое энергией активации E a . При абсолютной температуре T доля молекул, имеющих кинетическую энергию больше E a , может быть рассчитана из статистической механики . Понятие энергии активации объясняет экспоненциальный характер зависимости, и в той или иной форме оно присутствует во всех кинетических теориях.

Расчеты констант скорости реакции включают в себя усреднение энергии по распределению Максвелла–Больцмана с нижней границей и поэтому часто имеют вид неполных гамма-функций , которые оказываются пропорциональными . E a {\displaystyle E_{\text{a}}} e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}

Теория столкновения

Одним из подходов является теория столкновений химических реакций, разработанная Максом Траутцем и Уильямом Льюисом в 1916–18 годах. В этой теории предполагается, что молекулы реагируют, если они сталкиваются с относительной кинетической энергией вдоль линии их центров, которая превышает E a . Число бинарных столкновений между двумя разными молекулами в секунду на единицу объема определяется как [13] где N A — постоянная Авогадро , d AB — средний диаметр A и B , T — температура, которая умножается на постоянную Больцмана k B для преобразования в энергию, а μ AB — приведенная масса . z A B = N A d A B 2 8 π k B T μ A B , {\displaystyle z_{AB}=N_{\text{A}}d_{AB}^{2}{\sqrt {\frac {8\pi k_{\text{B}}T}{\mu _{AB}}}},}

Затем константа скорости рассчитывается как ⁠ ⁠ k = z A B e − E a R T {\displaystyle k=z_{AB}e^{\frac {-E_{\text{a}}}{RT}}} , так что теория столкновений предсказывает, что предэкспоненциальный множитель равен числу столкновений z AB . Однако для многих реакций это плохо согласуется с экспериментом, поэтому константа скорости записывается как ⁠ ⁠ k = ρ z A B e − E a R T {\displaystyle k=\rho z_{AB}e^{\frac {-E_{\text{a}}}{RT}}} . Вот эмпирический стерический множитель , часто намного меньше 1,00, который интерпретируется как доля достаточно энергичных столкновений, в которых две молекулы имеют правильную взаимную ориентацию для реакции. [13] ρ {\displaystyle \rho }

Теория переходного состояния

Уравнение Эйринга , еще одно выражение, похожее на Аррениус, появляется в « теории переходного состояния » химических реакций, сформулированной Юджином Вигнером , Генри Эйрингом , Майклом Полани и М. Г. Эвансом в 1930-х годах. Уравнение Эйринга можно записать так: где — энергия активации Гиббса, — энтропия активации , — энтальпия активации, — постоянная Больцмана , — постоянная Планка . [14] k = k B T h e − Δ G ‡ R T = k B T h e Δ S ‡ R e − Δ H ‡ R T , {\displaystyle k={\frac {k_{\text{B}}T}{h}}e^{-{\frac {\Delta G^{\ddagger }}{RT}}}={\frac {k_{\text{B}}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{-{\frac {\Delta H^{\ddagger }}{RT}}},} Δ G ‡ {\displaystyle \Delta G^{\ddagger }} Δ S ‡ {\displaystyle \Delta S^{\ddagger }} Δ H ‡ {\displaystyle \Delta H^{\ddagger }} k B {\displaystyle k_{\text{B}}} h {\displaystyle h}

На первый взгляд это выглядит как экспонента, умноженная на линейный по температуре фактор . Однако свободная энергия сама по себе является температурно-зависимой величиной. Свободная энергия активации представляет собой разность энтальпийного и энтропийного члена, умноженных на абсолютную температуру. Предэкспоненциальный множитель зависит в первую очередь от энтропии активации. Общее выражение снова принимает форму экспоненты Аррениуса (энтальпии, а не энергии), умноженной на медленно меняющуюся функцию T. Точная форма температурной зависимости зависит от реакции и может быть рассчитана с использованием формул из статистической механики, включающих функции распределения реагентов и активированного комплекса. Δ G ‡ = Δ H ‡ − T Δ S ‡ {\displaystyle \Delta G^{\ddagger }=\Delta H^{\ddagger }-T\Delta S^{\ddagger }}

Ограничения идеи энергии активации Аррениуса

Как энергия активации Аррениуса, так и константа скорости k определяются экспериментально и представляют собой макроскопические параметры реакции, которые не просто связаны с пороговыми энергиями и успешностью отдельных столкновений на молекулярном уровне. Рассмотрим конкретное столкновение (элементарную реакцию) между молекулами A и B. Угол столкновения, относительная поступательная энергия, внутренняя (особенно колебательная) энергия будут определять вероятность того, что столкновение произведет молекулу продукта AB. Макроскопические измерения E и k являются результатом многих отдельных столкновений с различными параметрами столкновения. Для исследования скоростей реакции на молекулярном уровне эксперименты проводятся в условиях, близких к столкновительным, и этот предмет часто называют динамикой молекулярной реакции. [15]

Другая ситуация, в которой объяснение параметров уравнения Аррениуса неудовлетворительно, — это гетерогенный катализ , особенно для реакций, которые демонстрируют кинетику Ленгмюра-Хиншельвуда . Очевидно, что молекулы на поверхности не «сталкиваются» напрямую, и простое молекулярное сечение здесь не применимо. Вместо этого предэкспоненциальный фактор отражает перемещение по поверхности к активному центру. [16]

Существуют отклонения от закона Аррениуса во время стеклования во всех классах стеклообразующих веществ. [17] Закон Аррениуса предсказывает, что движение структурных единиц (атомов, молекул, ионов и т. д.) должно замедляться с меньшей скоростью через стеклование, чем это экспериментально наблюдается. Другими словами, структурные единицы замедляются с большей скоростью, чем предсказывает закон Аррениуса. Это наблюдение становится разумным, если предположить, что единицы должны преодолеть энергетический барьер с помощью тепловой энергии активации. Тепловая энергия должна быть достаточно высокой, чтобы обеспечить поступательное движение единиц, что приводит к вязкому течению материала.

Смотрите также

Ссылки

  1. ^ аб Аррениус, SA (1889). «Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte». З. Физ. хим. 4 : 96–116 . doi :10.1515/зпч-1889-0408. S2CID  202553486.
  2. ^ аб Аррениус, SA (1889). «Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren». З. Физ. хим. 4 : 226–48 . doi :10.1515/zpch-1889-0416. S2CID  100032801.
  3. ^ Laidler, KJ (1984). «Развитие уравнения Аррениуса». J. Chem. Educ. 61 (6): 494– 498. Bibcode :1984JChEd..61..494L. doi :10.1021/ed061p494.
  4. ^ ab Laidler, KJ (1987) Химическая кинетика , Третье издание, Harper & Row, стр. 42
  5. ^ ab Kenneth Connors, Chemical Kinetics, 1990, VCH Publishers Chemical Kinetics: The Study of Reaction Rates in Solution в Google Books
  6. ^ Определение уравнения Аррениуса в Золотой книге ИЮПАК.
  7. ^ Силберберг, Мартин С. (2006). Химия (четвертое изд.). Нью-Йорк: McGraw-Hill. стр. 696. ISBN 0-07-111658-3.
  8. ^ Avery, HE (1974). "4. Зависимость скорости от температуры". Basic Reaction Kinetics and Mechanisms. Springer. pp.  47–58 . Получено 18 декабря 2023 г. Однако скорость реакции сильно зависит от температуры, поскольку для типичного процесса скорость удваивается или утраивается при повышении температуры на 10 °C.
  9. ^ "6.2.3.3: Закон Аррениуса – Энергии активации". Chemistry LibreTexts . 2013-10-02.
  10. ^ "15.2: Константа равновесия (K)". Chemistry LibreTexts . 2016-03-11 . Получено 2023-06-27 .
  11. ^ "Уравнение Аррениуса" (PDF) . Университет Пенсильвании . Получено 27 июня 2023 г. .
  12. ^ Определение модифицированного уравнения Аррениуса в Золотой книге ИЮПАК.
  13. ^ аб Лейдлер, Кейт Дж.; Мейзер, Джон Х. (1982). Физическая химия (1-е изд.). Бенджамин/Каммингс. стр.  376–78 . ISBN. 0-8053-5682-7.
  14. ^ Laidler, Keith J.; Meiser, John H. (1982). Физическая химия (1-е изд.). Benjamin/Cummings. стр.  378–83 . ISBN 0-8053-5682-7.
  15. ^ Левин, RD (2005) Молекулярная динамика реакций , Cambridge University Press
  16. ^ Слот, Тьерри К.; Райли, Натан; Шиджу, Н. Равеендран; Медлин, Дж. Уилл; Ротенберг, Гади (2020). «Экспериментальный подход к контролю эффектов ограничения на интерфейсах катализатора». Chemical Science . 11 (40): 11024– 11029. doi : 10.1039/D0SC04118A . ISSN  2041-6520. PMC 8162257 . PMID  34123192. 
  17. ^ Бауэр, Т.; Ланкенхаймер, П.; Лойдл, А. (2013). «Кооперативность и замораживание молекулярного движения при стекловании». Physical Review Letters . 111 (22): 225702. arXiv : 1306.4630 . Bibcode : 2013PhRvL.111v5702B. doi : 10.1103/PhysRevLett.111.225702. PMID  24329455. S2CID  13720989.

Библиография

  • Полинг, Л. К. (1988). Общая химия . Dover Publications.
  • Laidler, KJ (1987). Химическая кинетика (3-е изд.). Harper & Row.
  • Лейдлер, К. Дж. (1993). Мир физической химии . Oxford University Press.
  • Растворимость диоксида углерода в полиэтилене – использование уравнения Аррениуса для расчета растворимости видов в полимерах
Retrieved from "https://en.wikipedia.org/w/index.php?title=Arrhenius_equation&oldid=1259716654"