Арксинусное распределение
Тип распределения вероятностей
Арксинус
Функция плотности вероятности
Функция плотности вероятности для арксинусного распределения
Кумулятивная функция распределения
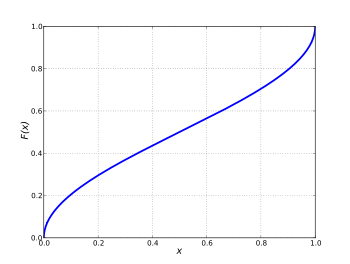Кумулятивная функция распределения для арксинуса
Параметрыникто
Поддерживать х ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]}
PDF ф ( х ) = 1 π х ( 1 − х ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}
СДФ Ф ( х ) = 2 π арксинус ⁡ ( х ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}
Иметь в виду 1 2 {\displaystyle {\frac {1}{2}}}
Медиана 1 2 {\displaystyle {\frac {1}{2}}}
Режим x ∈ { 0 , 1 } {\displaystyle x\in \{0,1\}}
Дисперсия 1 8 {\displaystyle {\tfrac {1}{8}}}
Асимметрия 0 {\displaystyle 0}
Избыточный эксцесс − 3 2 {\displaystyle -{\tfrac {3}{2}}}
Энтропия ln ⁡ π 4 {\displaystyle \ln {\tfrac {\pi }{4}}}
МГФ 1 + ∑ k = 1 ∞ ( ∏ r = 0 k − 1 2 r + 1 2 r + 2 ) t k k ! {\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}}
CF e i t 2 J 0 ( t 2 ) {\displaystyle e^{i{\frac {t}{2}}}J_{0}({\frac {t}{2}})}

В теории вероятностей распределение арксинуса — это распределение вероятностей, кумулятивная функция распределения которого включает арксинус и квадратный корень :

F ( x ) = 2 π arcsin ⁡ ( x ) = arcsin ⁡ ( 2 x − 1 ) π + 1 2 {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}}

для 0 ≤  x  ≤ 1, и чья функция плотности вероятности равна

f ( x ) = 1 π x ( 1 − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}

на (0, 1). Стандартное распределение арксинуса является частным случаем бета-распределения с α  =  β  = 1/2. То есть, если — случайная величина, распределенная по арксинусу, то . В более широком смысле распределение арксинуса является частным случаем распределения Пирсона типа I . X {\displaystyle X} X ∼ B e t a ( 1 2 , 1 2 ) {\displaystyle X\sim {\rm {Beta}}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}}

Распределение арксинуса появляется в законе арксинуса Леви , в законе арксинуса Эрдёша и как априорное распределение Джеффриса для вероятности успеха испытания Бернулли . [1] [2]

Обобщение

Арксинус – ограниченная поддержка
Параметры − ∞ < a < b < ∞ {\displaystyle -\infty <a<b<\infty \,}
Поддерживать x ∈ [ a , b ] {\displaystyle x\in [a,b]}
PDF f ( x ) = 1 π ( x − a ) ( b − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}
СДФ F ( x ) = 2 π arcsin ⁡ ( x − a b − a ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}
Иметь в виду a + b 2 {\displaystyle {\frac {a+b}{2}}}
Медиана a + b 2 {\displaystyle {\frac {a+b}{2}}}
Режим x ∈ a , b {\displaystyle x\in {a,b}}
Дисперсия 1 8 ( b − a ) 2 {\displaystyle {\tfrac {1}{8}}(b-a)^{2}}
Асимметрия 0 {\displaystyle 0}
Избыточный эксцесс − 3 2 {\displaystyle -{\tfrac {3}{2}}}
CF e i t b + a 2 J 0 ( b − a 2 t ) {\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)}

Произвольная ограниченная поддержка

Распределение можно расширить, включив в него любую ограниченную поддержку из a  ≤  x  ≤  b с помощью простого преобразования

F ( x ) = 2 π arcsin ⁡ ( x − a b − a ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}

для a  ≤  x  ≤  b , и чья функция плотности вероятности равна

f ( x ) = 1 π ( x − a ) ( b − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}

на ( а ,  б ).

Фактор формы

Обобщенное стандартное арксинусное распределение на (0,1) с функцией плотности вероятности

f ( x ; α ) = sin ⁡ π α π x − α ( 1 − x ) α − 1 {\displaystyle f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}}

также является частным случаем бета-распределения с параметрами . B e t a ( 1 − α , α ) {\displaystyle {\rm {Beta}}(1-\alpha ,\alpha )}

Обратите внимание, что общее распределение арксинуса сводится к стандартному распределению, указанному выше. α = 1 2 {\displaystyle \alpha ={\tfrac {1}{2}}}

Характеристики

  • Распределение арксинуса замкнуто относительно переноса и масштабирования на положительный множитель
    • Если X ∼ A r c s i n e ( a , b )   then  k X + c ∼ A r c s i n e ( a k + c , b k + c ) {\displaystyle X\sim {\rm {Arcsine}}(a,b)\ {\text{then }}kX+c\sim {\rm {Arcsine}}(ak+c,bk+c)}
  • Квадрат распределения арксинуса по (-1, 1) имеет распределение арксинуса по (0, 1)
    • Если X ∼ A r c s i n e ( − 1 , 1 )   then  X 2 ∼ A r c s i n e ( 0 , 1 ) {\displaystyle X\sim {\rm {Arcsine}}(-1,1)\ {\text{then }}X^{2}\sim {\rm {Arcsine}}(0,1)}
  • Координаты точек, равномерно выбранных на окружности радиуса с центром в начале координат (0, 0), имеют распределение r {\displaystyle r} A r c s i n e ( − r , r ) {\displaystyle {\rm {Arcsine}}(-r,r)}
    • Например, если мы выберем точку равномерно на окружности, то распределение координаты x точки будет равно , а распределение ее координаты y будет равно U ∼ U n i f o r m ( 0 , 2 π r ) {\displaystyle U\sim {\rm {Uniform}}(0,2\pi r)} r ⋅ cos ⁡ ( U ) ∼ A r c s i n e ( − r , r ) {\displaystyle r\cdot \cos(U)\sim {\rm {Arcsine}}(-r,r)} r ⋅ sin ⁡ ( U ) ∼ A r c s i n e ( − r , r ) {\textstyle r\cdot \sin(U)\sim {\rm {Arcsine}}(-r,r)}

Характерная функция

Характеристическая функция обобщенного арксинусного распределения представляет собой функцию Бесселя нулевого порядка первого рода, умноженную на комплексную экспоненту, заданную выражением . Для частного случая характеристическая функция принимает вид . e i t b + a 2 J 0 ( b − a 2 t ) {\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)} b = − a {\displaystyle b=-a} J 0 ( b t ) {\displaystyle J_{0}(bt)}

  • Если U и V — одинаковые равномерные (−π,π) случайные величины, то , , , и все имеют распределение. sin ⁡ ( U ) {\displaystyle \sin(U)} sin ⁡ ( 2 U ) {\displaystyle \sin(2U)} − cos ⁡ ( 2 U ) {\displaystyle -\cos(2U)} sin ⁡ ( U + V ) {\displaystyle \sin(U+V)} sin ⁡ ( U − V ) {\displaystyle \sin(U-V)} A r c s i n e ( − 1 , 1 ) {\displaystyle {\rm {Arcsine}}(-1,1)}
  • Если — обобщенное арксинусное распределение с параметром формы, поддерживаемым на конечном интервале [a,b], то X {\displaystyle X} α {\displaystyle \alpha } X − a b − a ∼ B e t a ( 1 − α , α )   {\displaystyle {\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\ }
  • Если X ~ Коши(0, 1), то имеет стандартное распределение арксинуса 1 1 + X 2 {\displaystyle {\tfrac {1}{1+X^{2}}}}

Ссылки

  1. ^ Overturf, Drew; et al. (2017). Исследование диаграмм направленности от объемно распределенных фазированных решеток . MILCOM 2017 - 2017 IEEE Military Communications Conference (MILCOM). стр. 817–822. doi :10.1109/MILCOM.2017.8170756. ISBN 978-1-5386-0595-0.
  2. ^ Бьюкенен, К. и др. (2020). «Управление нулевым лучом с использованием распределенных решеток и распределений с общей апертурой». Труды IEEE по антеннам и распространению . 68 (7): 5353–5364. doi :10.1109/TAP.2020.2978887.

Дальнейшее чтение

Retrieved from "https://en.wikipedia.org/w/index.php?title=Arcsine_distribution&oldid=1251766937"