Символ Леви-Чивиты

В математике , в частности в линейной алгебре , тензорном анализе и дифференциальной геометрии , символ Леви-Чивиты или эпсилон Леви-Чивиты представляет собой набор чисел, определяемых знаком перестановки натуральных чисел 1, 2, ..., n для некоторого положительного целого числа n . Он назван в честь итальянского математика и физика Туллио Леви-Чивиты . Другие названия включают символ перестановки , антисимметричный символ или чередующийся символ , которые относятся к его антисимметричному свойству и определению в терминах перестановок.

Стандартными буквами для обозначения символа Леви-Чивиты являются греческая строчная буква эпсилон ε или ϵ или, реже, латинская строчная буква e . Индексная нотация позволяет отображать перестановки способом, совместимым с тензорным анализом: где каждый индекс i ₁ , i ₂ , ..., i _n принимает значения 1, 2, ..., n . Существует n ⁿ индексированных значений ε _{i 1 i 2 ... i n} , которые можно организовать в n -мерный массив. Ключевым определяющим свойством символа является полная антисимметрия в индексах. Когда любые два индекса меняются местами, равны они или нет, символ инвертируется:$${\displaystyle \varepsilon _{i_{1}i_{2}\точки i_{n}}}$$$${\displaystyle \varepsilon _{\dots i_{p}\dots i_{q}\dots }=-\varepsilon _{\dots i_{q}\dots i_{p}\dots }.}$$

Если любые два индекса равны, символ равен нулю. Когда все индексы не равны, мы имеем: где p (называемый четностью перестановки) — это число попарных перестановок индексов, необходимых для расшифровки i ₁ , i ₂ , ..., i _n в порядке 1, 2, ..., n , а множитель (−1) ^p называется знаком или сигнатурой перестановки. Значение ε _{1 2 ... n} должно быть определено, иначе конкретные значения символа для всех перестановок неопределенны. Большинство авторов выбирают ε _{1 2 ... n} = +1 , что означает, что символ Леви-Чивиты равен знаку перестановки, когда все индексы не равны. Этот выбор используется на протяжении всей статьи.$${\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}=(-1)^{p}\varepsilon _{1\,2\,\dots n},}$$

Термин « n -мерный символ Леви-Чивиты» относится к тому факту, что число индексов в символе n соответствует размерности рассматриваемого векторного пространства, которое может быть евклидовым или неевклидовым , например , или пространством Минковского . Значения символа Леви-Чивиты не зависят от любого метрического тензора и системы координат . Кроме того, конкретный термин «символ» подчеркивает, что он не является тензором из-за того, как он преобразуется между системами координат; однако его можно интерпретировать как плотность тензора .${\displaystyle \mathbb {R} ^{3}}$

Символ Леви-Чивиты позволяет выразить определитель квадратной матрицы и векторное произведение двух векторов в трехмерном евклидовом пространстве в индексной нотации Эйнштейна .

Символ Леви-Чивита чаще всего используется в трех- и четырехмерном пространстве, а также в некоторой степени в двух измерениях, поэтому они приведены здесь до определения общего случая.

В двух измерениях символ Леви-Чивиты определяется следующим образом: Значения можно расположить в виде антисимметричной матрицы 2 × 2 :$${\displaystyle \varepsilon _{ij}={\begin{cases}+1&{\text{if}}(i,j)=(1,2)\\-1&{\text{if}}(i,j)=(2,1)\\\;\;\,0&{\text{if}}i=j\end{cases}}}$$$${\displaystyle {\begin{pmatrix}\varepsilon _{11} &\varepsilon _{12} \\\varepsilon _{21} &\varepsilon _{22}\end{pmatrix}} = {\begin{pmatrix} 0&1\\-1&0\end{pmatrix}}}$$

Использование двумерного символа распространено в конденсированном веществе и в некоторых специализированных высокоэнергетических темах, таких как суперсимметрия ^[1] и теория твисторов ^[2] , где он появляется в контексте 2- спиноров .

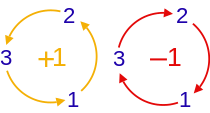
В трех измерениях символ Леви-Чивиты определяется следующим образом: ^[3]$${\displaystyle \varepsilon _{ijk}={\begin{cases}+1&{\text{если }}(i,j,k){\text{ равно }}(1,2,3),(2,3,1),{\text{ или }}(3,1,2),\\-1&{\text{если }}(i,j,k){\text{ равно }}(3,2,1),(1,3,2),{\text{ или }}(2,1,3),\\\;\;\,0&{\text{если }}i=j,{\text{ или }}j=k,{\text{ или }}k=i\end{cases}}}$$

То есть, ε _ijk равен 1, если ( i , j , k ) является четной перестановкой (1, 2, 3) , −1 , если это нечетная перестановка , и 0, если какой-либо индекс повторяется. Только в трех измерениях циклические перестановки (1, 2, 3) являются все четными перестановками, аналогично антициклические перестановки являются все нечетными перестановками. Это означает, что в 3d достаточно взять циклические или антициклические перестановки (1, 2, 3) и легко получить все четные или нечетные перестановки.

Аналогично двумерным матрицам, значения трехмерного символа Леви-Чивиты можно организовать в массив 3 × 3 × 3 :

где i — глубина ( синий : i = 1 ; красный : i = 2 ; зеленый : i = 3 ), j — строка, а k — столбец.

Вот несколько примеров:$${\displaystyle {\begin{aligned}\varepsilon _{\color {Кирпично-красный}{1}\color {Фиолетовый}{3}\color {Оранжевый}{2}}=-\varepsilon _{\color {Кирпично-красный}{1}\color {Оранжевый}{2}\color {Фиолетовый}{3}}&=-1\\\varepsilon _{\color {Фиолетовый}{3}\color {Кирпично-красный}{1}\color {Оранжевый}{2}}=-\varepsilon _{\color {Оранжевый}{2}\color {Кирпично-красный}{1}\color {Фиолетовый}{3}}&=-(-\varepsilon _{\color {Кирпично-красный}{1}\color {Оранжевый}{2}\color {Фиолетовый}{3}})=1\\\varepsilon _{\color {Оранжевый}{2}\color {Фиолетовый}{3}\color {КирпичноКрасный}{1}}=-\varepsilon _{\color {КирпичноКрасный}{1}\color {Фиолетовый}{3}\color {Оранжевый}{2}}&=-(-\varepsilon _{\color {КирпичноКрасный}{1}\color {Оранжевый}{2}\color {Фиолетовый}{3}})=1\\\varepsilon _{\color {Оранжевый}{2}\color {Фиолетовый}{3}\color {Оранжевый}{2}}=-\varepsilon _{\color {Оранжевый}{2}\color {Фиолетовый}{3}\color {Оранжевый}{2}}&=0\end{aligned}}}$$

В четырех измерениях символ Леви-Чивиты определяется следующим образом:$${\displaystyle \varepsilon _{ijkl}={\begin{cases}+1&{\text{если }}(i,j,k,l){\text{ является четной перестановкой }}(1,2,3,4)\\-1&{\text{если }}(i,j,k,l){\text{ является нечетной перестановкой }}(1,2,3,4)\\\;\;\,0&{\text{иначе}}\end{cases}}}$$

Эти значения можно организовать в массив 4 × 4 × 4 × 4 , хотя в 4-мерном и более измерениях это сложно изобразить.

Вот несколько примеров:$${\displaystyle {\begin{aligned}\varepsilon _{\color {BrickRed}{1}\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}&=-1\\\varepsilon _{\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}\color {Violet}{3}\color {RedViolet}{4}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}&=-1\\\varepsilon _{\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}}&=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}})=1\\\varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}=-\varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}&=0\end{aligned}}}$$

В более общем случае, в n измерениях , символ Леви-Чивиты определяется следующим образом: ^[4]$${\displaystyle \varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}={\begin{cases}+1&{\text{if }}(a_{1},a_{2},a_{3},\ldots ,a_{n}){\text{ is an even permutation of }}(1,2,3,\dots ,n)\\-1&{\text{if }}(a_{1},a_{2},a_{3},\ldots ,a_{n}){\text{ is an odd permutation of }}(1,2,3,\dots ,n)\\\;\;\,0&{\text{otherwise}}\end{cases}}}$$

Таким образом, это знак перестановки в случае перестановки и ноль в противном случае.

Используя заглавную букву пи Π для обычного умножения чисел, явное выражение для символа выглядит так: ^{[ необходима цитата ]} где функция signum (обозначаемая sgn ) возвращает знак своего аргумента, отбрасывая абсолютное значение, если оно не равно нулю. Формула верна для всех значений индекса и для любого n (когда n = 0 или n = 1 , это пустое произведение ). Однако вычисление формулы выше наивно имеет временную сложность O ( n ² ) , тогда как знак может быть вычислен из четности перестановки из ее непересекающихся циклов всего за O( n log( n )) затрат.$${\displaystyle {\begin{aligned}\varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}&=\prod _{1\leq i<j\leq n}\operatorname {sgn}(a_{j}-a_{i})\\&=\operatorname {sgn}(a_{2}-a_{1})\operatorname {sgn}(a_{3}-a_{1})\dotsm \operatorname {sgn}(a_{n}-a_{1})\operatorname {sgn}(a_{3}-a_{2})\operatorname {sgn}(a_{4}-a_{2})\dotsm \operatorname {sgn}(a_{n}-a_{2})\dotsm \operatorname {sgn}(a_{n}-a_{n-1})\end{aligned}}}$$

Тензор, компоненты которого в ортонормированном базисе задаются символом Леви-Чивиты (тензор ковариантного ранга n ), иногда называют тензором перестановки .

Согласно обычным правилам преобразования для тензоров символ Леви-Чивиты не изменяется при чистых вращениях, что согласуется с тем, что он (по определению) одинаков во всех системах координат, связанных ортогональными преобразованиями. Однако символ Леви-Чивиты является псевдотензором, поскольку при ортогональном преобразовании определителя Якоби −1, например, при отражении в нечетном числе измерений, он должен приобрести знак минус, если бы он был тензором. Поскольку он вообще не меняется, символ Леви-Чивиты по определению является псевдотензором.

Поскольку символ Леви-Чивиты является псевдотензором, результатом векторного произведения является псевдовектор , а не вектор. ^[5]

При общем изменении координат компоненты тензора перестановки умножаются на якобиан матрицы преобразования . Это означает, что в системах координат, отличных от той, в которой был определен тензор, его компоненты могут отличаться от компонентов символа Леви-Чивиты на общий множитель. Если система координат ортонормальная, множитель будет равен ±1 в зависимости от того, совпадает ли ориентация системы координат или нет. ^[5]

В безиндексной тензорной нотации символ Леви-Чивиты заменяется концепцией двойственного Ходжа . ^{[ необходима ссылка ]}

Символы суммирования можно исключить, используя обозначение Эйнштейна , где индекс, повторяющийся между двумя или более членами, указывает на суммирование по этому индексу. Например,

${\displaystyle \varepsilon _{ijk}\varepsilon ^{imn}\equiv \sum _{i=1,2,3}\varepsilon _{ijk}\varepsilon ^{imn}}$.

В следующих примерах используются обозначения Эйнштейна.

В двух измерениях, когда все i , j , m , n принимают значения 1 и 2: ^[3]

${\displaystyle \varepsilon _{ij}\varepsilon ^{mn}={\delta _{i}}^{m}{\delta _{j}}^{n}-{\delta _{i}}^{n}{\delta _{j}}^{m}}$

1

${\displaystyle \varepsilon _{ij}\varepsilon ^{in}={\delta _{j}}^{n}}$

2

${\displaystyle \varepsilon _{ij}\varepsilon ^{ij}=2.}$

3

В трех измерениях, когда все i , j , k , m , n принимают значения 1, 2 и 3: ^[3]

${\displaystyle \varepsilon _{ijk}\varepsilon ^{pqk}=\delta _{i}{}^{p}\delta _{j}{}^{q}-\delta _{i}{}^{q}\delta _{j}{}^{p}}$

4

${\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=2{\delta _{j}}^{i}}$

5

${\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=6.}$

6

Символ Леви-Чивиты связан с дельтой Кронекера . В трех измерениях эта связь задается следующими уравнениями (вертикальные линии обозначают определитель): ^[4]

${\displaystyle {\begin{aligned}\varepsilon _{ijk}\varepsilon _{lmn}&={\begin{vmatrix}\delta _{il}&\delta _{im}&\delta _{in}\\\delta _{jl}&\delta _{jm}&\delta _{jn}\\\delta _{kl}&\delta _{km}&\delta _{kn}\\\end{vmatrix}}\\[6pt]&=\delta _{il}\left(\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\right)-\delta _{im}\left(\delta _{jl}\delta _{kn}-\delta _{jn}\delta _{kl}\right)+\delta _{in}\left(\delta _{jl}\delta _{km}-\delta _{jm}\delta _{kl}\right).\end{aligned}}}$

Частный случай этого результата возникает, когда один из индексов повторяется и суммируется:

${\displaystyle \sum _{i=1}^{3}\varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}}$

В обозначениях Эйнштейна дублирование индекса i подразумевает сумму по i . Тогда предыдущее обозначается ε _ijk ε _imn = δ _jm δ _kn − δ _jn δ _km .

Если два индекса повторяются (и суммируются), это еще больше сокращается до:

${\displaystyle \sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ijk}\varepsilon _{ijn}=2\delta _{kn}}$

В n измерениях, когда все i ₁ , ..., i _n , j ₁ , ..., j _n принимают значения 1, 2, ..., n : ^{[ необходима цитата ]}

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{j_{1}\dots j_{n}}=\delta _{i_{1}\dots i_{n}}^{j_{1}\dots j_{n}}}$

7

${\displaystyle \varepsilon _{i_{1}\dots i_{k}~i_{k+1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{k}~j_{k+1}\dots j_{n}}=\delta _{i_{1}\ldots i_{k}~i_{k+1}\ldots i_{n}}^{i_{1}\dots i_{k}~j_{k+1}\ldots j_{n}}=k!~\delta _{i_{k+1}\dots i_{n}}^{j_{k+1}\dots j_{n}}}$

8

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{n}}=n!}$

9

где восклицательный знак ( ! ) обозначает факториал , а δ^{α ...}
_{β ...}является обобщенной дельтой Кронекера . Для любого n свойство

${\displaystyle \sum _{i,j,k,\dots =1}^{n}\varepsilon _{ijk\dots }\varepsilon _{ijk\dots }=n!}$

Из фактов следует, что

• каждая перестановка либо четная, либо нечетная,
• (+1) ² = (−1) ² = 1 , и
• число перестановок любого множества из n элементов равно ровно n !.

Частный случай ( 8 ) с есть${\textstyle k=n-2}$$${\displaystyle \varepsilon _{i_{1}\dots i_{n-2}jk}\varepsilon ^{i_{1}\dots i_{n-2}lm}=(n-2)!(\delta _{j}^{l}\delta _{k}^{m}-\delta _{j}^{m}\delta _{k}^{l})\,.}$$

В общем случае для n измерений можно записать произведение двух символов Леви-Чивиты как: Доказательство: Обе стороны меняют знаки при переключении двух индексов, поэтому без потери общности предположим . Если некоторые то левая сторона равна нулю, и правая сторона также равна нулю, поскольку две ее строки равны. Аналогично для . Наконец, если , то обе стороны равны 1.$${\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}\varepsilon _{j_{1}j_{2}\dots j_{n}}={\begin{vmatrix}\delta _{i_{1}j_{1}}&\delta _{i_{1}j_{2}}&\dots &\delta _{i_{1}j_{n}}\\\delta _{i_{2}j_{1}}&\delta _{i_{2}j_{2}}&\dots &\delta _{i_{2}j_{n}}\\\vdots &\vdots &\ddots &\vdots \\\delta _{i_{n}j_{1}}&\delta _{i_{n}j_{2}}&\dots &\delta _{i_{n}j_{n}}\\\end{vmatrix}}.}$$${\displaystyle i_{1}\leq \cdots \leq i_{n},j_{1}\leq \cdots \leq j_{n}}$${\displaystyle i_{c}=i_{c+1}}$${\displaystyle j_{c}=j_{c+1}}$${\displaystyle i_{1}<\cdots <i_{n},j_{1}<\cdots <j_{n}}$

Для ( 1 ) обе стороны антисимметричны относительно ij и mn . Поэтому нам нужно рассмотреть только случай i ≠ j и m ≠ n . Подстановкой мы видим, что уравнение справедливо для ε ₁₂ ε ¹² , то есть для i = m = 1 и j = n = 2 . (Обе стороны тогда равны одному). Поскольку уравнение антисимметрично относительно ij и mn , любой набор значений для них можно свести к приведенному выше случаю (который выполняется). Таким образом, уравнение справедливо для всех значений ij и mn .

Используя ( 1 ), имеем для ( 2 )

${\displaystyle \varepsilon _{ij}\varepsilon ^{in}=\delta _{i}{}^{i}\delta _{j}{}^{n}-\delta _{i}{}^{n}\delta _{j}{}^{i}=2\delta _{j}{}^{n}-\delta _{j}{}^{n}=\delta _{j}{}^{n}\,.}$

Здесь мы использовали соглашение Эйнштейна о суммировании , где i изменяется от 1 до 2. Далее, ( 3 ) следует аналогично из ( 2 ).

Чтобы установить ( 5 ), обратите внимание, что обе стороны обращаются в нуль, когда i ≠ j . Действительно, если i ≠ j , то нельзя выбрать m и n так, чтобы оба символа перестановки слева были ненулевыми. Тогда, при фиксированном i = j , есть только два способа выбрать m и n из оставшихся двух индексов. Для любых таких индексов мы имеем

${\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=\left(\varepsilon ^{imn}\right)^{2}=1}$

(без суммирования), и результат следующий.

Тогда ( 6 ) следует, поскольку 3! = 6 и для любых различных индексов i , j , k , принимающих значения 1, 2, 3 , мы имеем

${\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=1}$ (без суммирования, отдельные i , j , k )

В линейной алгебре определитель квадратной матрицы 3 × 3 A = [ a _ij ] можно записать ^[6]

${\displaystyle \det(\mathbf {A} )=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a_{1i}a_{2j}a_{3k}}$

Аналогично определитель матрицы A = [ a _ij ] размера n × n можно записать как ^[5]

${\displaystyle \det(\mathbf {A} )=\varepsilon _{i_{1}\dots i_{n}}a_{1i_{1}}\dots a_{ni_{n}},}$

где каждый i _r следует просуммировать по 1, ..., n или эквивалентно:

${\displaystyle \det(\mathbf {A} )={\frac {1}{n!}}\varepsilon _{i_{1}\dots i_{n}}\varepsilon _{j_{1}\dots j_{n}}a_{i_{1}j_{1}}\dots a_{i_{n}j_{n}},}$

где теперь каждый i _r и каждый j _r должны быть просуммированы по 1, ..., n . В более общем случае, мы имеем тождество ^[5]

${\displaystyle \sum _{i_{1},i_{2},\dots }\varepsilon _{i_{1}\dots i_{n}}a_{i_{1}\,j_{1}}\dots a_{i_{n}\,j_{n}}=\det(\mathbf {A} )\varepsilon _{j_{1}\dots j_{n}}}$

Пусть положительно ориентированный ортонормированный базис векторного пространства. Если ( a ¹ , a ² , a ³ ) и ( b ¹ , b ² , b ³ ) — координаты векторов a и b в этом базисе, то их векторное произведение можно записать в виде определителя: ^[5]${\displaystyle (\mathbf {e_{1}} ,\mathbf {e_{2}} ,\mathbf {e_{3}} )}$

${\displaystyle \mathbf {a\times b} ={\begin{vmatrix}\mathbf {e_{1}} &\mathbf {e_{2}} &\mathbf {e_{3}} \\a^{1}&a^{2}&a^{3}\\b^{1}&b^{2}&b^{3}\\\end{vmatrix}}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}\mathbf {e} _{i}a^{j}b^{k}}$

отсюда также использование символа Леви-Чивиты, и более просто:

${\displaystyle (\mathbf {a\times b} )^{i}=\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a^{j}b^{k}.}$

В обозначениях Эйнштейна символы суммирования могут быть опущены, а i -й компонент их векторного произведения равен ^[4]

${\displaystyle (\mathbf {a\times b} )^{i}=\varepsilon _{ijk}a^{j}b^{k}.}$

Первый компонент — это

${\displaystyle (\mathbf {a\times b} )^{1}=a^{2}b^{3}-a^{3}b^{2}\,,}$

затем с помощью циклических перестановок 1, 2, 3 остальные могут быть получены немедленно, без явного вычисления их по приведенным выше формулам:

${\displaystyle {\begin{aligned}(\mathbf {a\times b} )^{2}&=a^{3}b^{1}-a^{1}b^{3}\,,\\(\mathbf {a\times b} )^{3}&=a^{1}b^{2}-a^{2}b^{1}\,.\end{aligned}}}$

Из приведенного выше выражения для векторного произведения имеем:

${\displaystyle \mathbf {a\times b} =-\mathbf {b\times a} }$.

Если c = ( c ¹ , c ² , c ³ ) — третий вектор, то тройное скалярное произведение равно

${\displaystyle \mathbf {a} \cdot (\mathbf {b\times c} )=\varepsilon _{ijk}a^{i}b^{j}c^{k}.}$

Из этого выражения видно, что тройное скалярное произведение антисимметрично при перестановке любой пары аргументов. Например,

${\displaystyle \mathbf {a} \cdot (\mathbf {b\times c} )=-\mathbf {b} \cdot (\mathbf {a\times c} )}$.

Если F = ( F ¹ , F ² , F ³ ) — векторное поле, определенное на некотором открытом множестве как функция положения x = ( x ¹ , x ² , x ³ ) ( используя декартовы координаты ). Тогда i -й компонент ротора F равен [ ^4]${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle (\nabla \times \mathbf {F} )^{i}(\mathbf {x} )=\varepsilon _{ijk}{\frac {\partial }{\partial x^{j}}}F^{k}(\mathbf {x} ),}$

что следует из выражения векторного произведения выше, заменяя компоненты оператора вектора градиента (набла).

В любой произвольной криволинейной системе координат и даже при отсутствии метрики на многообразии символ Леви-Чивиты, как он определен выше, может рассматриваться как поле плотности тензора двумя различными способами. Его можно рассматривать как контравариантную плотность тензора веса +1 или как ковариантную плотность тензора веса −1. В n измерениях, используя обобщенную дельту Кронекера, ^{[7] [8]}

${\displaystyle {\begin{aligned}\varepsilon ^{\mu _{1}\dots \mu _{n}}&=\delta _{\,1\,\dots \,n}^{\mu _{1}\dots \mu _{n}}\,\\\varepsilon _{\nu _{1}\dots \nu _{n}}&=\delta _{\nu _{1}\dots \nu _{n}}^{\,1\,\dots \,n}\,.\end{aligned}}}$

Обратите внимание, что они численно идентичны. В частности, знак тот же.

На псевдоримановом многообразии можно определить координатно-инвариантное ковариантное тензорное поле, координатное представление которого согласуется с символом Леви-Чивиты везде, где система координат такова, что базис касательного пространства ортонормален относительно метрики и соответствует выбранной ориентации. Этот тензор не следует путать с упомянутым выше полем плотности тензора. Представление в этом разделе близко следует Carroll 2004.

Ковариантный тензор Леви-Чивиты (также известный как риманова форма объема ) в любой системе координат, которая соответствует выбранной ориентации, равен

${\displaystyle E_{a_{1}\dots a_{n}}={\sqrt {\left|\det[g_{ab}]\right|}}\,\varepsilon _{a_{1}\dots a_{n}}\,,}$

где g _ab — представление метрики в этой системе координат. Аналогично мы можем рассмотреть контравариантный тензор Леви-Чивиты, подняв индексы с метрикой, как обычно,

${\displaystyle E^{a_{1}\dots a_{n}}=E_{b_{1}\dots b_{n}}\prod _{i=1}^{n}g^{a_{i}b_{i}}={\frac {1}{\sqrt {\left|\det[g_{ab}]\right|}}}\,\epsilon ^{a_{1}\dots a_{n}},,}$

но обратите внимание, что если метрическая сигнатура содержит нечетное число отрицательных собственных значений q , то знак компонентов этого тензора отличается от стандартного символа Леви-Чивиты: ^[9]

${\displaystyle E^{a_{1}\dots a_{n}}={\frac {\operatorname {sgn} \left(\det[g_{ab}]\right)}{\sqrt {\left|\det[g_{ab}]\right|}}}\,\varepsilon _{a_{1}\dots a_{n}},}$

где sgn(det[g _ab ]) = (−1) ^q , — это обычный символ Леви-Чивиты, обсуждаемый в оставшейся части этой статьи, и мы использовали определение метрического определителя при выводе. Более конкретно, когда тензор и базисная ориентация выбраны так, что , мы имеем .${\displaystyle \varepsilon _{a_{1}\dots a_{n}}}$${\textstyle E_{01\dots n}=+{\sqrt {\left|\det[g_{ab}]\right|}}}$${\displaystyle E^{01\dots n}={\frac {\operatorname {sgn}(\det[g_{ab}])}{\sqrt {\left|\det[g_{ab}]\right|}}}}$

Из этого мы можем сделать вывод о личности,

${\displaystyle E^{\mu _{1}\dots \mu _{p}\alpha _{1}\dots \alpha _{n-p}}E_{\mu _{1}\dots \mu _{p}\beta _{1}\dots \beta _{n-p}}=(-1)^{q}p!\delta _{\beta _{1}\dots \beta _{n-p}}^{\alpha _{1}\dots \alpha _{n-p}}\,,}$

где

${\displaystyle \delta _{\beta _{1}\dots \beta _{n-p}}^{\alpha _{1}\dots \alpha _{n-p}}=(n-p)!\delta _{\beta _{1}}^{\lbrack \alpha _{1}}\dots \delta _{\beta _{n-p}}^{\alpha _{n-p}\rbrack }}$

обобщенная дельта Кронекера.

В пространстве Минковского (четырехмерном пространстве-времени специальной теории относительности ) ковариантный тензор Леви-Чивиты имеет вид

${\displaystyle E_{\alpha \beta \gamma \delta }=\pm {\sqrt {\left|\det[g_{\mu \nu }]\right|}}\,\varepsilon _{\alpha \beta \gamma \delta }\,,}$

где знак зависит от ориентации базиса. Контравариантный тензор Леви-Чивиты есть

${\displaystyle E^{\alpha \beta \gamma \delta }=g^{\alpha \zeta }g^{\beta \eta }g^{\gamma \theta }g^{\delta \iota }E_{\zeta \eta \theta \iota }\,.}$

Ниже приведены примеры общего тождества, приведенного выше, специализированного для пространства Минковского (с отрицательным знаком, возникающим из-за нечетного числа отрицательных знаков в сигнатуре метрического тензора в любом соглашении о знаках):

${\displaystyle {\begin{aligned}E_{\alpha \beta \gamma \delta }E_{\rho \sigma \mu \nu }&=-g_{\alpha \zeta }g_{\beta \eta }g_{\gamma \theta }g_{\delta \iota }\delta _{\rho \sigma \mu \nu }^{\zeta \eta \theta \iota }\\E^{\alpha \beta \gamma \delta }E^{\rho \sigma \mu \nu }&=-g^{\alpha \zeta }g^{\beta \eta }g^{\gamma \theta }g^{\delta \iota }\delta _{\zeta \eta \theta \iota }^{\rho \sigma \mu \nu }\\E^{\alpha \beta \gamma \delta }E_{\alpha \beta \gamma \delta }&=-24\\E^{\alpha \beta \gamma \delta }E_{\rho \beta \gamma \delta }&=-6\delta _{\rho }^{\alpha }\\E^{\alpha \beta \gamma \delta }E_{\rho \sigma \gamma \delta }&=-2\delta _{\rho \sigma }^{\alpha \beta }\\E^{\alpha \beta \gamma \delta }E_{\rho \sigma \theta \delta }&=-\delta _{\rho \sigma \theta }^{\alpha \beta \gamma }\,.\end{aligned}}}$

• Список тем перестановок
• Симметричный тензор

• Мизнер, К.; Торн, К. С.; Уилер, Дж. А. (1973). Гравитация . W. H. Freeman & Co. стр.  85–86 , §3.5. ISBN 0-7167-0344-0.
• Нойеншвандер, DE (2015). Тензорное исчисление по физике . Издательство Университета Джонса Хопкинса. стр. 11, 29, 95. ISBN. 978-1-4214-1565-9.
• Кэрролл, Шон М. (2004), Пространство-время и геометрия, Addison-Wesley, ISBN 0-8053-8732-3

В данной статье использованы материалы из символа перестановки Леви-Чивиты на PlanetMath , лицензированные по лицензии Creative Commons Attribution/Share-Alike License .

• Вайсштейн, Эрик В. «Тензор перестановок». Математический мир .