Антисимметричное отношение

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Antisymmetric relation" – news · newspapers · books · scholar · JSTOR (January 2010) (Learn how and when to remove this message)

Транзитивные  бинарные отношения в т е
Симметричный Антисимметричный Подключен Обоснованный Имеет соединения Имеет встречает Рефлексивный Нерефлексивный Асимметричный Всего, Полуконнекc Антирефлексивный ​ Отношение эквивалентности Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Предварительный заказ (квазизаказ) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Частичный заказ ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Всего предзаказов ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Общий заказ ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Предварительный заказ ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Хорошо-квази-упорядочение ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Хорошо упорядоченный ✗ Y Y Y ✗ ✗ Y ✗ ✗ Решетка ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-полурешетка ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Встреча-полурешетка ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Строгий частичный порядок ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Строгий слабый порядок ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Строгий общий порядок ✗ Y Y ✗ ✗ ✗ ✗ Y Y Симметричный Антисимметричный Подключен Обоснованный Имеет соединения Имеет встречает Рефлексивный Нерефлексивный Асимметричный Определения, для всех и${\displaystyle a,b}$${\displaystyle S\neq \varnothing :}$ ${\displaystyle {\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}\min S\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle aRa}$ ${\displaystyle {\text{not }}aRa}$ ${\displaystyle {\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}}$
Yуказывает, что свойство столбца всегда верно для термина строки (слева), в то время как ✗ указывает, что свойство не гарантируется в общем случае (оно может выполняться, а может и не выполняться). Например, то, что каждое отношение эквивалентности симметрично, но не обязательно антисимметрично, обозначается в столбце «Симметрично» и ✗ в столбце «Антисимметрично» соответственно.Y Все определения неявно требуют, чтобы однородное отношение было транзитивным : для всех, если и то Определение термина может требовать дополнительных свойств, которые не перечислены в этой таблице.${\displaystyle R}$${\displaystyle a,b,c,}$${\displaystyle aRb}$${\displaystyle bRc}$${\displaystyle aRc.}$

В математике бинарное отношение на множестве является антисимметричным, если не существует пары различных элементов, каждый из которых связан с другим. Более формально, является антисимметричным точно, если для всех или, что эквивалентно, Определение антисимметрии ничего не говорит о том, выполняется ли на самом деле или нет для любого . Антисимметричное отношение на множестве может быть рефлексивным (то есть для всех ), иррефлексивным (то есть ни для одного ) или ни рефлексивным, ни иррефлексивным. Отношение является асимметричным тогда и только тогда, когда оно является одновременно антисимметричным и иррефлексивным.${\displaystyle R}$ ${\displaystyle X}$${\displaystyle X}$${\displaystyle R}$${\displaystyle R}$${\displaystyle a,b\in X,}$$${\displaystyle {\text{if }}\,aRb\,{\text{ with }}\,a\neq b\,{\text{ then }}\,bRa\,{\text{ must not hold}},}$$$${\displaystyle {\text{if }}\,aRb\,{\text{ and }}\,bRa\,{\text{ then }}\,a=b.}$$${\displaystyle aRa}$${\displaystyle a}$${\displaystyle R}$${\displaystyle X}$${\displaystyle aRa}$${\displaystyle a\in X}$${\displaystyle aRa}$${\displaystyle a\in X}$

Отношение делимости натуральных чисел является важным примером антисимметричного отношения. В этом контексте антисимметрия означает, что единственный способ, которым каждое из двух чисел может делиться на другое, — это если два числа на самом деле являются одним и тем же числом; эквивалентно, если и различны и является множителем , то не может быть множителем Например, 12 делится на 4, но 4 не делится на 12.${\displaystyle n}$${\displaystyle m}$${\displaystyle n}$${\displaystyle m,}$${\displaystyle m}$${\displaystyle n.}$

Обычное отношение порядка на действительных числах является антисимметричным: если для двух действительных чисел и выполняются оба неравенства и , то и должны быть равны. Аналогично, порядок подмножеств на подмножествах любого заданного множества является антисимметричным: даны два множества и если каждый элемент в также находится в и каждый элемент в также находится в , то и должны содержать все те же элементы и, следовательно, быть равными: Реальным примером отношения, которое обычно является антисимметричным, является «оплаченный счет в ресторане» (понимаемый как ограниченный данным случаем). Обычно некоторые люди оплачивают свои собственные счета, в то время как другие платят за своих супругов или друзей. Пока никакие два человека не оплачивают счета друг друга, отношение является антисимметричным.${\displaystyle \,\leq \,}$${\displaystyle x}$${\displaystyle y}$ ${\displaystyle x\leq y}$${\displaystyle y\leq x}$${\displaystyle x}$${\displaystyle y}$ ${\displaystyle \,\subseteq \,}$${\displaystyle A}$${\displaystyle B,}$${\displaystyle A}$${\displaystyle B}$${\displaystyle B}$${\displaystyle A,}$${\displaystyle A}$${\displaystyle B}$$${\displaystyle A\subseteq B{\text{ and }}B\subseteq A{\text{ implies }}A=B}$$

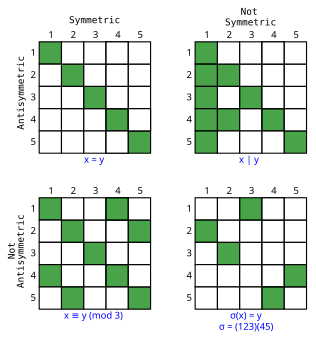
Частичные и полные порядки антисимметричны по определению. Отношение может быть как симметричным , так и антисимметричным (в этом случае оно должно быть корефлексивным ), и существуют отношения, которые не являются ни симметричными, ни антисимметричными (например, отношение «охотится на» на биологические виды ).

Антисимметрия отличается от асимметрии : отношение асимметрично тогда и только тогда, когда оно антисимметрично и иррефлексивно .

• Рефлексивное отношение  – бинарное отношение, которое связывает каждый элемент с самим собой.
• Симметрия в математике

• Вайсштейн, Эрик В. «Антисимметричное отношение». MathWorld .
• Липшуц, Сеймур ; Марк Ларс Липсон (1997). Теория и проблемы дискретной математики . McGraw-Hill. стр. 33. ISBN 0-07-038045-7.
• nLab антисимметричное отношение