Воздушная масса (солнечная энергия)
Коэффициент воздушной массы определяет прямую оптическую длину пути через атмосферу Земли , выраженную как отношение к длине пути вертикально вверх, т. е. в зените . Коэффициент воздушной массы может быть использован для характеристики солнечного спектра после того, как солнечное излучение прошло через атмосферу.
Коэффициент воздушной массы обычно используется для характеристики производительности солнечных элементов в стандартизированных условиях и часто обозначается с помощью синтаксиса «AM» с последующим числом. «AM1.5» является почти универсальным при характеристике наземных электрогенерирующих панелей .
Описание
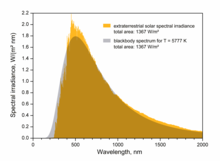
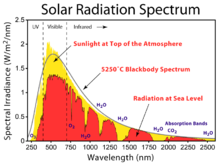
Общая интенсивность солнечного излучения подобна интенсивности излучения абсолютно черного тела того же размера при температуре около 5800 К. [1] При прохождении через атмосферу солнечный свет ослабляется за счет рассеяния и поглощения ; чем через большую толщу атмосферы он проходит, тем сильнее ослабляется .
По мере того, как солнечный свет проходит через атмосферу, химические вещества взаимодействуют с солнечным светом и поглощают определенные длины волн, изменяя количество коротковолнового света, достигающего поверхности Земли. Более активным компонентом этого процесса является водяной пар, что приводит к широкому спектру полос поглощения на многих длинах волн, в то время как молекулярный азот, кислород и углекислый газ добавляются к этому процессу. К тому времени, как он достигает поверхности Земли, спектр строго ограничен между дальним инфракрасным и ближним ультрафиолетовым.
Атмосферное рассеяние играет роль в удалении более высоких частот из прямого солнечного света и рассеивании его по небу. [2] Вот почему небо кажется голубым, а солнце желтым — больше высокочастотного синего света достигает наблюдателя через непрямые рассеянные пути; и меньше синего света следует по прямому пути, придавая солнцу желтый оттенок. [3] Чем больше расстояние в атмосфере, через которое проходит солнечный свет, тем сильнее этот эффект, поэтому солнце выглядит оранжевым или красным на рассвете и закате, когда солнечный свет проходит очень наклонно через атмосферу — постепенно все больше синего и зеленого удаляется из прямых лучей, придавая солнцу оранжевый или красный вид; и небо кажется розовым — потому что синий и зеленый рассеиваются по таким длинным путям, что они сильно ослабевают, прежде чем достичь наблюдателя, что приводит к характерному розовому небу на рассвете и закате.
Определение
Для длины пути через атмосферу и солнечного излучения, падающего под углом относительно нормали к поверхности Земли, коэффициент воздушной массы равен: [4]
| ( А.1 ) |
где - длина пути в зените (т.е. по нормали к поверхности Земли) на уровне моря .
Таким образом, количество воздушных масс зависит от высоты траектории движения Солнца по небу и, следовательно, меняется в зависимости от времени суток, смены сезонов года и широты наблюдателя.
Расчет

Приближение первого порядка для воздушной массы определяется выражением
| ( А.1 ) |
где — зенитный угол , обычно в градусах.
Вышеуказанное приближение не учитывает конечную высоту атмосферы и предсказывает бесконечную массу воздуха на горизонте. Однако оно достаточно точно для значений до 75°. Было предложено несколько уточнений для более точного моделирования толщины пути к горизонту, например, предложенное Кастеном и Янгом (1989): [5]
| ( А.2 ) |
Более полный список таких моделей представлен в основной статье Airmass , для различных атмосферных моделей и экспериментальных наборов данных. На уровне моря воздушная масса по направлению к горизонту ( = 90°) составляет приблизительно 38. [6]
Моделирование атмосферы как простой сферической оболочки дает разумное приближение: [7]
| ( А.3 ) |
где радиус Земли = 6371 км, эффективная высота атмосферы ≈ 9 км, а их отношение ≈ 708. Чтобы избежать разности двух больших чисел, это можно записать как
что также показывает сходство с простой формулой, приведенной выше.
Сравнение этих моделей приведено в таблице ниже:
| Плоская Земля | Кастен и Янг | Сферическая оболочка | |
|---|---|---|---|
| степень | ( А.1 ) | ( А.2 ) | ( А.3 ) |
| 0° | 1.0 | 1.0 | 1.0 |
| 60° | 2.0 | 2.0 | 2.0 |
| 70° | 2.9 | 2.9 | 2.9 |
| 75° | 3.9 | 3.8 | 3.8 |
| 80° | 5.8 | 5.6 | 5.6 |
| 85° | 11.5 | 10.3 | 10.6 |
| 88° | 28.7 | 19.4 | 20.3 |
| 90° | 37.9 | 37.6 |
Эти простые модели предполагают, что для этих целей атмосфера может считаться эффективно сконцентрированной в районе нижних 9 км, [8] т.е. по сути все атмосферные эффекты обусловлены атмосферной массой в нижней половине тропосферы . Это полезная и простая модель при рассмотрении атмосферных эффектов на интенсивность солнечного излучения.
Можно также предположить, что плотность воздуха падает экспоненциально с высотой. Если x — это расстояние вдоль светового луча от места его пересечения с землей, деленное на эквивалентную толщину атмосферы (примерно 9 км), то высота точки равна:
Тогда воздушная масса составит:
где — дополнительная функция ошибок . Это дает более низкое значение, около 33, когда солнце находится на горизонте. Однако ни эта модель, ни предыдущая не учитывают искривление световых лучей из-за рефракции (см. Выравнивание ). Более реалистичная модель будет основана на барометрической формуле для плотности.
Случаи
- АМ0
Спектр за пределами атмосферы обозначается как «AM0», что означает «нулевая атмосфера». Солнечные элементы, используемые для космических энергетических приложений, например, на спутниках связи , обычно характеризуются с помощью AM0.
- АМ1
Спектр после прохождения через атмосферу до уровня моря с солнцем прямо над головой по определению обозначается как «AM1». Это означает «одна атмосфера». Диапазон от AM1 ( =0°) до AM1.1 ( =25°) является полезным для оценки производительности солнечных элементов в экваториальных и тропических регионах.
- АМ1.5
Солнечные панели обычно не работают при толщине ровно одной атмосферы: если солнце находится под углом к поверхности Земли, эффективная толщина будет больше. Многие из крупнейших мировых центров населения, а значит, и солнечные установки и промышленность в Европе, Китае, Японии, Соединенных Штатах Америки и других местах (включая северную Индию, юг Африки и Австралию) находятся в умеренных широтах. Поэтому число AM, представляющее спектр в средних широтах, встречается гораздо чаще.
«AM1.5», толщина атмосферы 1,5, соответствует углу солнечного зенита = 48,2°. В то время как летнее число AM для средних широт в средние части дня составляет менее 1,5, более высокие числа применяются утром и вечером, а также в другие времена года. Поэтому AM1.5 полезно для представления общего годового среднего значения для средних широт. Конкретное значение 1,5 было выбрано в 1970-х годах в целях стандартизации на основе анализа данных о солнечной радиации в соседних Соединенных Штатах. [9] С тех пор солнечная промышленность использует AM1.5 для всех стандартизированных испытаний или оценок наземных солнечных элементов или модулей, включая те, которые используются в концентрирующих системах. Последними стандартами AM1.5, относящимися к фотоэлектрическим приложениям, являются ASTM G-173 [10] [11] и IEC 60904, все из которых получены на основе моделирования, полученного с помощью кода SMARTS .
Освещенность для дневного света ( данная версия ) в соответствии с AM1.5 составляет 109 870 люкс (что соответствует спектру AM1.5 до 1000,4 Вт/м2 ) .
- AM2~3
Диапазон AM2 ( =60°) - AM3 ( =70°) полезен для оценки общей средней производительности солнечных элементов, установленных в высоких широтах, например, в Северной Европе. Аналогично диапазон AM2 - AM3 полезен для оценки производительности в зимнее время в умеренных широтах, например, коэффициент воздушной массы больше 2 в любое время суток зимой на широтах до 37°.
- АМ38
Обычно AM38 рассматривается как воздушная масса в горизонтальном направлении ( =90°, т.е. закат) на уровне моря. [6] Однако на практике наблюдается высокая степень изменчивости интенсивности солнечного излучения, получаемого под углами, близкими к горизонту, как описано в следующем разделе «Интенсивность солнечного излучения».
- На больших высотах
Относительная воздушная масса является функцией только зенитного угла солнца и, следовательно, не меняется с местной высотой. Наоборот, абсолютная воздушная масса, равная относительной воздушной массе, умноженной на местное атмосферное давление и деленной на стандартное (на уровне моря) давление, уменьшается с высотой над уровнем моря. Для солнечных панелей, установленных на больших высотах, например, в регионе Альтиплано , можно использовать более низкие абсолютные числа AM, чем для соответствующей широты на уровне моря: числа AM менее 1 по направлению к экватору и, соответственно, более низкие числа, чем перечисленные выше, для других широт. Однако этот подход является приблизительным и не рекомендуется. Лучше всего моделировать фактический спектр на основе относительной воздушной массы (например, 1,5) и фактических атмосферных условий для конкретной высоты рассматриваемого участка.
Интенсивность солнечной радиации
Интенсивность солнечного излучения на коллекторе уменьшается с увеличением коэффициента воздушной массы, но из-за сложных и переменных атмосферных факторов, вовлеченных в процесс, не простым или линейным образом. Например, почти все высокоэнергетическое излучение удаляется в верхних слоях атмосферы (между AM0 и AM1), и поэтому AM2 не вдвое хуже AM1. Кроме того, существует большая изменчивость многих факторов, способствующих атмосферному затуханию, [12], таких как водяной пар, аэрозоли, фотохимический смог и эффекты температурных инверсий . В зависимости от уровня загрязнения воздуха общее затухание может изменяться до ±70% по направлению к горизонту, что значительно влияет на производительность, особенно по направлению к горизонту, где эффекты нижних слоев атмосферы усиливаются во много раз.
Одна из эмпирических аппроксимационных моделей солнечной интенсивности в зависимости от воздушной массы имеет вид: [13] [14]
| ( И.1 ) |
где интенсивность солнечного излучения вне атмосферы Земли = 1,353 кВт/м 2 , а коэффициент 1,1 выведен из предположения, что диффузная составляющая составляет 10% от прямой составляющей. [13]
Эта формула хорошо вписывается в средний диапазон ожидаемой изменчивости, связанной с загрязнением:
| ЯВЛЯЮСЬ | диапазон из-за загрязнения [12] | формула ( I.1 ) | ASTM G-173 [11] | |
|---|---|---|---|---|
| степень | Вт/м 2 | Вт/м 2 | Вт/м 2 | |
| - | 0 | 1367 [15] | 1353 | 1347,9 [16] |
| 0° | 1 | 840 .. 1130 = 990 ± 15% | 1040 | |
| 23° | 1.09 | 800 .. 1110 = 960 ± 16% [17] | 1020 | |
| 30° | 1.15 | 780 .. 1100 = 940 ± 17% | 1010 | |
| 45° | 1.41 | 710 .. 1060 = 880 ± 20% [17] | 950 | |
| 48,2° | 1.5 | 680 .. 1050 = 870 ± 21% [17] | 930 | 1000,4 [18] |
| 60° | 2 | 560 .. 970 = 770 ± 27% | 840 | |
| 70° | 2.9 | 430 .. 880 = 650 ± 34% [17] | 710 | |
| 75° | 3.8 | 330 .. 800 = 560 ± 41% [17] | 620 | |
| 80° | 5.6 | 200 .. 660 = 430 ± 53% | 470 | |
| 85° | 10 | 85 .. 480 = 280 ± 70% | 270 | |
| 90° | 38 | 20 |
Это иллюстрирует, что значительная мощность доступна всего на нескольких градусах над горизонтом. Например, когда солнце находится более чем на 60° над горизонтом ( <30°), интенсивность солнечного излучения составляет около 1000 Вт/м 2 (из уравнения I.1 , как показано в таблице выше), тогда как когда солнце находится всего на 15° над горизонтом ( =75°), интенсивность солнечного излучения все еще составляет около 600 Вт/м 2 или 60% от своего максимального уровня; и всего на 5° над горизонтом все еще 27% от максимума.
На больших высотах
Приблизительная модель увеличения интенсивности с высотой и точностью до нескольких километров над уровнем моря выглядит следующим образом: [13] [19]
| ( И.2 ) |
где - высота солнечного коллектора над уровнем моря в км, - воздушная масса (из А.2 ), как если бы коллектор был установлен на уровне моря.
В качестве альтернативы, учитывая значительную практическую изменчивость, для оценки AM можно применить однородную сферическую модель , используя:
| ( А.4 ) |
где нормализованные высоты атмосферы и коллектора составляют соответственно ≈ 708 (как и выше) и .
И затем приведенную выше таблицу или соответствующее уравнение ( I.1 или I.3 или I.4 для среднего, загрязненного или чистого воздуха соответственно) можно использовать для оценки интенсивности по АМ обычным способом.
Эти приближения в I.2 и A.4 подходят для использования только на высотах в несколько километров над уровнем моря, подразумевая, что они снижают производительность до уровней AM0 только около 6 и 9 км соответственно. Напротив, большая часть ослабления высокоэнергетических компонентов происходит в озоновом слое - на больших высотах около 30 км. [20] Следовательно, эти приближения подходят только для оценки производительности наземных коллекторов.
Эффективность солнечных батарей
Атмосфера Земли поглощает значительное количество ультрафиолетового света. Результирующий спектр на поверхности Земли имеет меньше фотонов, но они имеют в среднем более низкую энергию, поэтому количество фотонов, превышающих запрещенную зону , на единицу энергии солнечного света больше, чем в космосе. Это означает, что солнечные элементы более эффективны при AM1, чем при AM0. Этот, по-видимому, противоречащий интуиции результат возникает просто потому, что кремниевые элементы не могут в полной мере использовать высокоэнергетическое излучение, которое отфильтровывает атмосфера. Как показано ниже, даже несмотря на то, что эффективность ниже при AM0, общая выходная мощность ( P out ) для типичного солнечного элемента по-прежнему самая высокая при AM0. И наоборот, форма спектра существенно не меняется с дальнейшим увеличением толщины атмосферы, и, следовательно, эффективность элемента существенно не меняется для чисел AM выше 1.
| ЯВЛЯЮСЬ | Интенсивность солнечной радиации | Выходная мощность | Эффективность |
|---|---|---|---|
| P в Вт/м 2 | P вых Вт/м 2 | Выход P / Вход P | |
| 0 | 1350 | 160 | 12% |
| 1 | 1000 | 150 | 15% |
| 2 | 800 | 120 | 15% |
Это иллюстрирует более общую точку зрения, что, учитывая, что солнечная энергия «бесплатна», и если доступное пространство не является ограничением, другие факторы, такие как общая выходная мощность P out и P out на единицу вложенных денег (например, на доллар), часто являются более важными соображениями, чем эффективность ( P out /P in ).
Смотрите также
Примечания и ссылки
- ^ или точнее 5777 К, как сообщается в NASA Solar System Exploration - Sun: Facts & Figures Архивировано 03.07.2015 на Wayback Machine, получено 27 апреля 2011 г. "Эффективная температура ... 5777 К"
- ^ См. также статью Рассеянное излучение неба .
- ^ Желтый — это цвет, отрицательный по отношению к синему. Желтый — это совокупный цвет того, что остается после того, как рассеяние удаляет часть синего из «белого» света солнца.
- ^ Питер Вюрфель (2005). Физика солнечных батарей . Вайнхайм: Wiley-VCH. ISBN 3-527-40857-6 .
- ^ Кастен, Ф. и Янг, А. Т. (1989). Пересмотренные таблицы оптических воздушных масс и аппроксимационная формула. Прикладная оптика 28:4735–4738.
- ^ ab Основная статья Airmass сообщает значения в диапазоне от 36 до 40 для различных атмосферных моделей.
- ^ Шенберг, Э. (1929). Теоретическая фотометрия, ж) Сверхвымирание живых существ в Эрдатмосфере. В справочнике по астрофизике . Группа II, раньше Hälfte. Берлин: Шпрингер.
- ^ Основная статья Airmass сообщает значения в диапазоне от 8 до 10 км для различных атмосферных моделей.
- ^ Gueymard, C.; Myers, D.; Emery, K. (2002). «Предлагаемые эталонные спектры облученности для тестирования систем солнечной энергии». Solar Energy . 73 (6): 443–467. Bibcode :2002SoEn...73..443G. doi :10.1016/S0038-092X(03)00005-7.
- ^ Справочная информация о спектральной солнечной радиации: воздушная масса 1,5 NREL, получено 1 мая 2011 г.
- ^ ab Справочная спектральная плотность солнечного излучения: ASTM G-173 ASTM получено 1 мая 2011 г.
- ^ ab Планирование и установка фотоэлектрических систем: руководство для установщиков, архитекторов и инженеров , 2-е изд. (2008), Таблица 1.1, Earthscan совместно с Международным институтом окружающей среды и развития , Deutsche Gesellschaft für Sonnenergie. ISBN 1-84407-442-0 .
- ^ abc PVCDROM получено 1 мая 2011 г., Стюарт Боуден и Кристиана Хонсберг, Solar Power Labs, Университет штата Аризона
- ^ Мейнел, AB и Мейнел, MP (1976). Прикладная солнечная энергия Addison Wesley Publishing Co.
- ^ В справочнике Earthscan в качестве интенсивности солнечного излучения за пределами атмосферы используется значение 1367 Вт/м 2 .
- ^ Стандарт ASTM G-173 измеряет интенсивность солнечного излучения в диапазоне от 280 до 4000 нм .
- ^ abcde Интерполировано из данных справочника Earthscan с использованием подходящих вариантов оценки методом наименьших квадратов уравнения I.1 :
- для загрязненного воздуха:
( И.3 ) - для чистого воздуха:
( И.4 ) - ^ Стандарт ASTM G-173 измеряет интенсивность солнечного излучения в условиях «сельской аэрозольной нагрузки», т.е. в условиях чистого воздуха, — таким образом, стандартное значение близко к максимуму ожидаемого диапазона.
- ^ Лауэ, Э.Г. (1970), Измерение спектральной солнечной радиации на различных высотах над уровнем моря, Солнечная энергия , т. 13, № 1, стр. 43-50, IN1-IN4, 51-57, 1970.
- ^ RLF Boyd (Ed.) (1992). Астрономическая фотометрия: руководство , раздел 6.4. Kluwer Academic Publishers. ISBN 0-7923-1653-3 .


















![{\displaystyle I=1,1\times I_{\mathrm {o} }\times [(1-h/7,1)0,7^{(AM)^{0,678})}+h/7,1]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8398f4bddfe3dde983c935eeb7ab5c1cc2a40de2)





