Аффинная симметрическая группа

Аффинные симметрические группы — это семейство математических структур, описывающих симметрии числовой прямой и правильной треугольной мозаики плоскости, а также связанные с ними объекты более высокой размерности. В дополнение к этому геометрическому описанию аффинные симметрические группы могут быть определены другими способами: как наборы перестановок (перестановок) целых чисел ( ..., −2, −1, 0, 1, 2, ... ), которые являются периодическими в определенном смысле, или в чисто алгебраических терминах как группа с определенными генераторами и соотношениями . Они изучаются в комбинаторике и теории представлений .

Конечная симметрическая группа состоит из всех перестановок конечного множества. Каждая аффинная симметрическая группа является бесконечным расширением конечной симметрической группы. Многие важные комбинаторные свойства конечных симметрических групп могут быть расширены до соответствующих аффинных симметрических групп. Статистика перестановок, такая как спуски и инверсии, может быть определена в аффинном случае. Как и в конечном случае, естественные комбинаторные определения для этих статистик также имеют геометрическую интерпретацию.

Аффинные симметрические группы имеют тесные связи с другими математическими объектами, включая схемы жонглирования и некоторые сложные группы отражений . Многие из их комбинаторных и геометрических свойств распространяются на более широкое семейство аффинных групп Коксетера .

Аффинную симметрическую группу можно эквивалентно определить как абстрактную группу посредством генераторов и соотношений или в терминах конкретных геометрических и комбинаторных моделей. ^[1]

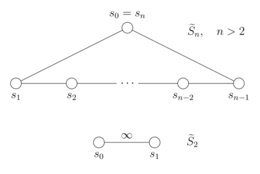
Один из способов определения групп — это генераторы и отношения . В этом типе определения генераторы — это подмножество элементов группы, которые при объединении производят все остальные элементы. Отношения определения — это система уравнений, которая определяет, когда две комбинации генераторов равны. ^{[a] [2]} Таким образом, аффинная симметрическая группа генерируется набором из n элементов, которые удовлетворяют следующим отношениям: когда ,${\displaystyle {\widetilde {S}}_{n}}$$${\displaystyle s_{0},s_{1},\ldots ,s_{n-1}}$$${\displaystyle n\geq 3}$

1. ${\displaystyle s_{i}^{2}=1}$(генераторы — инволюции ),
2. ${\displaystyle s_{i}s_{j}=s_{j}s_{i}}$если j не является одним из , что указывает на то, что для этих пар генераторов групповая операция коммутативна , и${\displaystyle i-1,i,i+1}$
3. ${\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}$.

В приведенных выше соотношениях индексы берутся по модулю n , так что третье соотношение включает в себя как частный случай . (Второе и третье соотношение иногда называют соотношениями кос . ^[3] ) Когда , аффинная симметрическая группа является бесконечной диэдральной группой, порожденной двумя элементами, подчиняющимися только соотношениям . ^[4]${\displaystyle s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}}$${\displaystyle n=2}$${\displaystyle {\widetilde {S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$

Эти отношения можно переписать в специальной форме, которая определяет группы Коксетера , так что аффинные симметричные группы являются группами Коксетера, с их порождающими множествами Коксетера. ^[4] Каждая группа Коксетера может быть представлена ​​диаграммой Коксетера–Дынкина , в которой вершины соответствуют образующим, а ребра кодируют отношения между ними. ^[5] Для диаграмма Коксетера–Дынкина представляет собой n -цикл (где ребра соответствуют отношениям между парами последовательных образующих, а отсутствие ребра между другими парами образующих указывает на то, что они коммутируют), тогда как для она состоит из двух узлов, соединенных ребром, помеченным . ^{[6] [4]}${\displaystyle s_{i}}$${\displaystyle n\geq 3}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle n=2}$${\displaystyle \infty}$

В евклидовом пространстве с координатами множество точек V , для которых образует (гипер)плоскость , ( n − 1) -мерное подпространство. Для каждой пары различных элементов i и j из и каждого целого числа k множество точек в V , которые удовлетворяют, образует ( n − 2) -мерное подпространство внутри V , и существует единственное отражение V , которое фиксирует это подпространство. Тогда аффинная симметрическая группа может быть реализована геометрически как набор отображений из V в себя, композиций этих отражений. ^[7]${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (x_{1},\ldots ,x_{n})}$${\displaystyle x_{1}+x_{2}+\cdots +x_{n}=0}$${\displaystyle \{1,\ldots ,n\}}$${\displaystyle x_{i}-x_{j}=k}$${\displaystyle {\widetilde {S}}_{n}}$

Внутри V подмножество точек с целочисленными координатами образует корневую решетку , Λ . Это множество всех целочисленных векторов, таких что . ^[8] Каждое отражение сохраняет эту решетку, и, таким образом, решетка сохраняется всей группой. ^[9]${\displaystyle (a_{1},\ldots ,a_{n})}$${\displaystyle a_{1}+\cdots +a_{n}=0}$

Фиксированные подпространства этих отражений делят V на конгруэнтные симплексы , называемые альковами . ^[10] Ситуация, когда показана на рисунке; ​​в этом случае корневая решетка является треугольной решеткой, отражающие линии делят V на равносторонние треугольные альковы, а корни являются центрами неперекрывающихся шестиугольников, составленных из шести треугольных альковов. ^{[11] [12]}${\displaystyle n=3}$

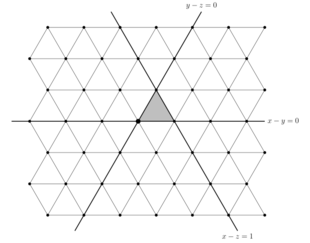
Для перевода между геометрическими и алгебраическими определениями фиксируется ниша и рассматриваются n гиперплоскостей, которые образуют ее границу. Отражения через эти граничные гиперплоскости можно отождествить с генераторами Коксетера. В частности, существует уникальная ниша ( фундаментальная ниша ), состоящая из точек, таких что , которая ограничена гиперплоскостями ..., и проиллюстрирована в случае . Для можно отождествить отражение через с генератором Коксетера , а также отождествить отражение через с генератором . ^[10]${\displaystyle (x_{1},\ldots ,x_{n})}$${\displaystyle x_{1}\geq x_{2}\geq \cdots \geq x_{n}\geq x_{1}-1}$${\displaystyle x_{1}-x_{2}=0,}$ ${\displaystyle x_{2}-x_{3}=0,}$${\displaystyle x_{1}-x_{n}=1,}$${\displaystyle n=3}$${\displaystyle i=1,\ldots ,n-1}$${\displaystyle x_{i}-x_{i+1}=0}$${\displaystyle s_{i}}$${\displaystyle x_{1}-x_{n}=1}$${\displaystyle s_{0}=s_{n}}$

Элементы аффинной симметрической группы могут быть реализованы как группа периодических перестановок целых чисел. В частности, говорят, что функция является аффинной перестановкой, если${\ displaystyle u \ двоеточие \ mathbb {Z} \ to \ mathbb {Z} }$

• это биекция (каждое целое число появляется как значение ровно для одного ),${\displaystyle и(х)}$${\displaystyle x}$
• ${\displaystyle и(х+n)=и(х)+n}$для всех целых чисел x (функция эквивариантна относительно сдвига на ), и${\displaystyle n}$
• ${\displaystyle u(1)+u(2)+\cdots +u(n)=1+2+\cdots +n={\frac {n(n+1)}{2}}}$, -е треугольное число .${\displaystyle n}$

Для каждой аффинной перестановки и, в более общем смысле, для каждой биекции с эквивариантным сдвигом все числа должны быть различны по модулю n . Аффинная перестановка однозначно определяется ее оконной нотацией , поскольку все другие значения могут быть найдены путем сдвига этих значений. Таким образом, аффинные перестановки также могут быть идентифицированы с кортежами целых чисел, которые содержат один элемент из каждого класса конгруэнтности по модулю n и в сумме дают . ^[13]${\displaystyle u(1),\ldots ,u(n)}$ ${\displaystyle [u(1),\ldots ,u(n)]}$${\displaystyle u}$ ${\displaystyle [u(1),\ldots ,u(n)]}$${\displaystyle 1+2+\cdots +n}$

Для перевода между комбинаторными и алгебраическими определениями, для можно идентифицировать генератор Коксетера с аффинной перестановкой, которая имеет нотацию окна , а также идентифицировать генератор с аффинной перестановкой . В более общем смысле, каждое отражение (то есть сопряжение одного из генераторов Коксетера) может быть описано однозначно следующим образом: для различных целых чисел i , j в и произвольного целого числа k оно отображает i в j − kn , отображает j в i + kn и фиксирует все входные данные, не конгруэнтные i или j по модулю n . ^[14]${\displaystyle i=1,\ldots ,n-1}$${\displaystyle s_{i}}$${\displaystyle [1,2,\ldots ,i-1,i+1,i,i+2,\ldots ,n]}$${\displaystyle s_{0}=s_{n}}$${\displaystyle [0,2,3,\ldots ,n-2,n-1,n+1]}$${\displaystyle \{1,\ldots ,n\}}$

Аффинные перестановки можно представить как бесконечные периодические матрицы перестановок . ^[15] Если — аффинная перестановка, соответствующая матрица имеет запись 1 в позиции в бесконечной сетке для каждого целого числа i , а все остальные записи равны 0. Поскольку u — биекция, результирующая матрица содержит ровно одну 1 в каждой строке и столбце. Условие периодичности на карте u гарантирует, что запись в позиции равна записи в позиции для каждой пары целых чисел . ^[15] Например, часть матрицы для аффинной перестановки показана на рисунке. В строке 1 есть 1 в столбце 2; в строке 2 есть 1 в столбце 0; и в строке 3 есть 1 в столбце 4. Остальные записи в этих строках и столбцах все равны 0, и все остальные записи в матрице фиксируются условием периодичности.${\displaystyle u:\mathbb {Z} \to \mathbb {Z}}$${\displaystyle (я,u(я))}$${\displaystyle \mathbb {Z} \times \mathbb {Z} }$${\displaystyle (а,б)}$${\displaystyle (a+n,b+n)}$${\displaystyle (а,б)}$${\displaystyle [2,0,4]\in {\widetilde {S}}_{3}}$

Аффинная симметрическая группа содержит конечную симметрическую группу перестановок элементов как подгруппу и факторгруппу . [ ^16] Эти связи допускают прямой перевод между комбинаторными и геометрическими определениями аффинной симметрической группы.${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle n}$

Существует канонический способ выбора подгруппы , изоморфной конечной симметрической группе . В терминах алгебраического определения это подгруппа , порожденная (исключая простое отражение ). Геометрически это соответствует подгруппе преобразований, которые фиксируют начало координат, в то время как комбинаторно это соответствует оконным обозначениям, для которых (то есть, в которых оконное обозначение является однострочной записью конечной перестановки). ^{[17] [18]}${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle s_{1},\ldots ,s_{n-1}}$${\displaystyle s_{0}=s_{n}}$${\displaystyle \{u(1),\ldots ,u(n)\}=\{1,2,\ldots ,n\}}$

Если — оконная запись элемента этой стандартной копии , то его действие на гиперплоскость V в задается перестановкой координат: . ^[19] (В этой статье геометрическое действие перестановок и аффинных перестановок находится справа; таким образом, если u и v — две аффинные перестановки, то действие uv на точку задается первым применением u , а затем применением v .)${\displaystyle u=[u(1),u(2),\ldots ,u(n)]}$${\displaystyle S_{n}\subset {\widetilde {S}}_{n}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (x_{1},x_{2},\ldots ,x_{n})\cdot u=(x_{u(1)},x_{u(2)},\ldots ,x_{u(n)})}$

Существует также много нестандартных копий , содержащихся в . Геометрическое построение заключается в выборе любой точки a в Λ (то есть целочисленного вектора, сумма координат которого равна 0); подгруппа изометрий , фиксирующих a , изоморфна . ^[20]${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle ({\widetilde {S}}_{n})_{a}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle S_{n}}$

Существует простое отображение (технически, сюръективный групповой гомоморфизм ) π из на конечную симметрическую группу . В терминах комбинаторного определения аффинная перестановка может быть отображена в перестановку путем сокращения элементов окна по модулю n до элементов , оставляя однострочную запись перестановки. ^[21] В этой статье образ аффинной перестановки u называется базовой перестановкой u .${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle \{1,2,\ldots ,n\}}$${\displaystyle \pi (u)}$

Отображение π отправляет генератор Коксетера в перестановку, однострочная нотация и циклическая нотация которой имеют вид и , соответственно. ^{[22] [21]}${\displaystyle s_{0}=[0,2,3,4,\ldots ,n-2,n-1,n+1]}$${\displaystyle [n,2,3,4,\ldots ,n-2,n-1,1]}$${\displaystyle (1\;n)}$

Ядро π по определению является множеством аффинных перестановок, лежащей в основе перестановки тождества . Оконные обозначения таких аффинных перестановок имеют вид , где — целочисленный вектор такой, что , то есть, где . Геометрически это ядро ​​состоит из трансляций , изометрий, которые сдвигают все пространство V без его вращения или отражения. ^[23] В злоупотреблении обозначениями символ Λ используется в этой статье для всех трех этих множеств (целочисленные векторы в V , аффинные перестановки с лежащей в основе перестановкой тождества и трансляции); во всех трех случаях операция естественной группы превращает Λ в абелеву группу , свободно генерируемую n − 1 векторами . [ ^24]${\displaystyle [1-a_{1}\cdot n,2-a_{2}\cdot n,\ldots ,n-a_{n}\cdot n]}$${\displaystyle (a_{1},a_{2},\ldots ,a_{n})}$${\displaystyle a_{1}+a_{2}+\ldots +a_{n}=0}$${\displaystyle (a_{1},\ldots ,a_{n})\in \Lambda }$${\displaystyle \{(1,-1,0,\ldots ,0),(0,1,-1,\ldots ,0),\ldots ,(0,\ldots ,0,1,-1)\}}$

Аффинная симметрическая группа имеет Λ в качестве нормальной подгруппы и изоморфна полупрямому произведению этой подгруппы с конечной симметрической группой , где действие на Λ осуществляется перестановкой координат. Следовательно, каждый элемент u из имеет единственную реализацию как произведение , где является перестановкой в ​​стандартной копии в и является переносом в Λ . ^[25]${\displaystyle {\widetilde {S}}_{n}}$$${\displaystyle {\widetilde {S}}_{n}\cong S_{n}\ltimes \Lambda }$$${\displaystyle S_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle u=r\cdot t}$${\displaystyle r}$${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle t}$

Эта точка зрения допускает прямой перевод между комбинаторными и геометрическими определениями : если записать, где и тогда аффинная перестановка u соответствует жесткому движению V, определяемому формулой ^[25]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle [u(1),\ldots ,u(n)]=[r_{1}-a_{1}\cdot n,\ldots ,r_{n}-a_{n}\cdot n]}$${\displaystyle r=[r_{1},\ldots ,r_{n}]=\pi (u)}$${\displaystyle (a_{1},a_{2},\ldots ,a_{n})\in \Lambda }$$${\displaystyle (x_{1},\ldots ,x_{n})\cdot u=\left(x_{r(1)}+a_{1},\ldots ,x_{r(n)}+a_{n}\right).}$$

Более того, как и в случае любой аффинной группы Коксетера, аффинная симметрическая группа действует транзитивно и свободно на множестве альковов: для каждых двух альковов уникальный элемент группы переводит один альков в другой. ^[26] Следовательно, произвольный выбор алькова ставит группу во взаимно-однозначное соответствие с альковами: единичный элемент соответствует , а каждый другой элемент группы g соответствует алькову , который является образом под действием g . ^[27]${\displaystyle A_{0}}$${\displaystyle A_{0}}$${\displaystyle A=A_{0}\cdot g}$${\displaystyle A_{0}}$

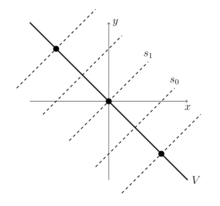
Алгебраически, это бесконечная диэдральная группа, порожденная двумя образующими, подчиненными соотношениям . ^[4] Каждый другой элемент группы может быть записан как знакопеременное произведение копий и . ^[28]${\displaystyle {\widetilde {S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$${\displaystyle s_{0}}$${\displaystyle s_{1}}$

Комбинаторно аффинная перестановка имеет нотацию окна , соответствующую биекции для каждого целого числа k . Аффинная перестановка имеет нотацию окна , соответствующую биекции для каждого целого числа k . Другие элементы имеют следующие нотации окна:${\displaystyle s_{1}}$${\displaystyle [2,1]}$${\displaystyle 2k\mapsto 2k-1,2k-1\mapsto 2k}$${\displaystyle s_{0}}$${\displaystyle [0,3]}$${\displaystyle 2k\mapsto 2k+1,2k+1\mapsto 2k}$

${\displaystyle {\begin{aligned}\overbrace {s_{0}s_{1}\cdots s_{0}s_{1}} ^{2k{\text{ factors}}}&=[1+2k,2-2k],\\[5pt]\overbrace {s_{1}s_{0}\cdots s_{1}s_{0}} ^{2k{\text{ factors}}}&=[1-2k,2+2k],\\[5pt]\overbrace {s_{0}s_{1}\cdots s_{0}} ^{2k+1{\text{ factors}}}&=[2+2k,1-2k],\\[5pt]\overbrace {s_{1}s_{0}\cdots s_{1}} ^{2k+1{\text{ factors}}}&=[2-2(k+1),1+2(k+1)].\end{aligned}}}$

Геометрически пространство V, на котором действует, является прямой с бесконечным числом равноотстоящих отражений. ^[29] Естественно отождествить прямую V с действительной прямой , с отражением вокруг точки 0 и с отражением вокруг точки 1. В этом случае отражение отражается через точку – k для любого целого числа k , композиция переносит прямую на –2 , а композиция переносит прямую на 2. ^{[30] [29} ]${\displaystyle {\widetilde {S}}_{2}}$${\displaystyle \mathbb {R} ^{1}}$${\displaystyle s_{0}}$${\displaystyle s_{1}}$${\displaystyle (s_{0}s_{1})^{k}s_{0}}$${\displaystyle s_{0}s_{1}}$${\displaystyle s_{1}s_{0}}$

Многие статистики перестановок и другие особенности комбинаторики конечных перестановок можно распространить на аффинный случай. ^[31]

Длина элемента g группы Коксетера G — это наименьшее число k, такое что g можно записать как произведение k генераторов Коксетера группы G . ^{[32] Геометрически} длина элемента g в — это число отражающих гиперплоскостей, которые разделяют и , где — фундаментальная ниша (симплекс, ограниченный отражающими гиперплоскостями генераторов Коксетера ). ^{[b] [33]} Комбинаторно длина аффинной перестановки кодируется в терминах соответствующего понятия инверсий : для аффинной перестановки u длина равна ^[34] Альтернативно, это число классов эквивалентности пар таких, что и при отношении эквивалентности, если для некоторого целого числа k . Производящая функция для длины в равна ^{[35] [36]}${\displaystyle \ell (g)}$${\displaystyle g=s_{i_{1}}\cdots s_{i_{k}}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot g}$${\displaystyle A_{0}}$${\displaystyle s_{0},s_{1},\ldots ,s_{n-1}}$$${\displaystyle \ell (u)=\#\left\{(i,j)\colon i\in \{1,\ldots ,n\},i<j,{\text{ and }}u(i)>u(j)\right\}.}$$${\displaystyle (i,j)\in \mathbb {Z} \times \mathbb {Z} }$${\displaystyle i<j}$${\displaystyle u(i)>u(j)}$${\displaystyle (i,j)\equiv (i',j')}$${\displaystyle (i-i',j-j')=(kn,kn)}$${\displaystyle {\widetilde {S}}_{n}}$$${\displaystyle \sum _{g\in {\widetilde {S}}_{n}}q^{\ell (g)}={\frac {1-q^{n}}{(1-q)^{n}}}.}$$

Аналогично, существует аффинный аналог спусков в перестановках: аффинная перестановка u имеет спуск в позиции i, если . (В силу периодичности u имеет спуск в позиции i тогда и только тогда, когда он имеет спуск в позиции для всех целых чисел k .) Алгебраически спуски соответствуют правым спускам в смысле групп Кокстера; то есть i является спуском u тогда и только тогда, когда . ^[37] Левые спуски (то есть те индексы i, что ) являются спусками обратной аффинной перестановки ; эквивалентно, они являются значениями i, такими, что i встречается перед i − 1 в последовательности . ^[38] Геометрически i является спуском u тогда и только тогда, когда фиксированная гиперплоскость разделяет ниши и ^[39]${\displaystyle u(i)>u(i+1)}$${\displaystyle i+kn}$${\displaystyle \ell (u\cdot s_{i})<\ell (u)}$${\displaystyle \ell (s_{i}\cdot u)<\ell (u)}$${\displaystyle u^{-1}}$ ${\displaystyle \ldots ,u(-2),u(-1),u(0),u(1),u(2),\ldots }$${\displaystyle s_{i}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot u.}$

Поскольку существует только конечное число возможностей для числа спусков аффинной перестановки, но бесконечное число аффинных перестановок, невозможно наивно сформировать производящую функцию для аффинных перестановок по числу спусков (аффинный аналог многочленов Эйлера ). ^[40] Одним из возможных решений является рассмотрение аффинных спусков (эквивалентно, циклических спусков) в конечной симметрической группе . ^[11] Другим является одновременное рассмотрение длины и числа спусков аффинной перестановки. Многомерная производящая функция для этих статистик по одновременно для всех n равна , где des( w ) — число спусков аффинной перестановки w , а — q -экспоненциальная функция . ^[41]${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$$${\displaystyle \sum _{n\geq 1}{\frac {x^{n}}{1-q^{n}}}\sum _{w\in {\widetilde {S}}_{n}}t^{\operatorname {des} (w)}q^{\ell (w)}=\left[{\frac {x\cdot {\frac {\partial }{\partial {x}}}\log(\exp(x;q))}{1-t\exp(x;q)}}\right]_{x\mapsto x{\frac {1-t}{1-q}}}}$$${\displaystyle \exp(x;q)=\sum _{n\geq 0}{\frac {x^{n}(1-q)^{n}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}}$

Любая биекция разбивает целые числа на (возможно бесконечный) список (возможно бесконечных) циклов: для каждого целого числа i цикл, содержащий i, является последовательностью , где возведение в степень представляет функциональную композицию. Для аффинной перестановки u следующие условия эквивалентны: все циклы u конечны, u имеет конечный порядок , и геометрическое действие u на пространстве V имеет по крайней мере одну неподвижную точку. ^[42]${\displaystyle u:\mathbb {Z} \to \mathbb {Z} }$${\displaystyle (\ldots ,u^{-2}(i),u^{-1}(i),i,u(i),u^{2}(i),\ldots )}$

Длина отражения элемента u из — это наименьшее число k , такое что существуют отражения, такие что . (В симметрической группе отражения являются транспозициями, а длина отражения перестановки u равна , где — количество циклов u . ^[16] ) В (Lewis et al. 2019) была доказана следующая формула для длины отражения аффинной перестановки u : для каждого цикла u определите вес как целое число k, такое что последовательные записи, конгруэнтные по модулю n, отличаются ровно на kn . Сформируйте кортеж весов циклов u (подсчитывая трансляции одного и того же цикла на кратные n только один раз) и определите нулевое значение как размер наименьшего разбиения множества этого кортежа так, чтобы каждая часть в сумме давала 0. Тогда длина отражения u равна , где — базовая перестановка u . ^[43]${\displaystyle \ell _{R}(u)}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle r_{1},\ldots ,r_{k}}$${\displaystyle u=r_{1}\cdots r_{k}}$${\displaystyle n-c(u)}$${\displaystyle c(u)}$ ${\displaystyle \nu (u)}$$${\displaystyle \ell _{R}(u)=n-2\nu (u)+c(\pi (u)),}$$${\displaystyle \pi (u)}$

Для каждой аффинной перестановки u существует выбор подгруппы W такой , что , , и для стандартной формы, подразумеваемой этим полупрямым произведением, длины отражений являются аддитивными, то есть . [ ^20]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle W\cong S_{n}}$${\displaystyle {\widetilde {S}}_{n}=W\ltimes \Lambda }$${\displaystyle u=w\cdot t}$${\displaystyle \ell _{R}(u)=\ell _{R}(w)+\ell _{R}(t)}$

Приведенное слово для элемента g группы Коксетера — это кортеж генераторов Коксетера минимально возможной длины такой, что . ^[32] Элемент g называется полностью коммутативным, если любое приведенное слово может быть преобразовано в любое другое путем последовательной перестановки пар коммутирующих множителей. ^[44] Например, в конечной симметрической группе элемент является полностью коммутативным, так как два его приведенных слова и могут быть соединены путем перестановки коммутирующих множителей, но не является полностью коммутативным, так как нет способа достичь приведенного слова, начиная с приведенного слова путем перестановок. ^[45]${\displaystyle (s_{i_{1}},\ldots ,s_{i_{\ell (g)}})}$${\displaystyle g=s_{i_{1}}\cdots s_{i_{\ell (g)}}}$${\displaystyle S_{4}}$${\displaystyle 2143=(12)(34)}$${\displaystyle (s_{1},s_{3})}$${\displaystyle (s_{3},s_{1})}$${\displaystyle 4132=(142)(3)}$${\displaystyle (s_{3},s_{2},s_{3},s_{1})}$${\displaystyle (s_{2},s_{3},s_{2},s_{1})}$

Билли, Джокуш и Стэнли (1993) доказали, что в конечной симметрической группе перестановка полностью коммутативна тогда и только тогда, когда она избегает шаблона перестановки 321, то есть тогда и только тогда, когда ее однострочная запись не содержит трехчленной убывающей подпоследовательности. В (Green 2002) этот результат был распространен на аффинные перестановки: аффинная перестановка u полностью коммутативна тогда и только тогда, когда не существует целых чисел, таких что . ^[c]${\displaystyle S_{n}}$${\displaystyle i<j<k}$${\displaystyle u(i)>u(j)>u(k)}$

Число аффинных перестановок, избегающих одного шаблона p , конечно тогда и только тогда, когда p избегает шаблона 321, ^[47], так что, в частности, существует бесконечно много полностью коммутативных аффинных перестановок. Они были перечислены по длине в (Hanusa & Jones 2010).

Параболические подгруппы и их представители смежных классов предлагают богатую комбинаторную структуру. Другие аспекты аффинных симметричных групп, такие как их порядок Брюа и теория представлений , также могут быть поняты с помощью комбинаторных моделей. ^[31]${\displaystyle {\widetilde {S}}_{n}}$

Стандартная параболическая подгруппа группы Коксетера — это подгруппа, порождённая подмножеством её порождающего множества Коксетера. [ ^48] Максимальные параболические подгруппы — это те, которые получаются путём исключения одного порождающего множества Коксетера. В все максимальные параболические подгруппы изоморфны конечной симметрической группе . Подгруппа, порождённая подмножеством, состоит из тех аффинных перестановок, которые стабилизируют интервал , то есть отображают каждый элемент этого интервала в другой элемент интервала. ^[37]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle \{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}}$${\displaystyle [i+1,i+n]}$

Для фиксированного элемента i из , пусть будет максимальным собственным подмножеством генераторов Кокстера, исключая , и пусть обозначает параболическую подгруппу, порожденную J . Каждый смежный класс имеет уникальный элемент минимальной длины. Набор таких представителей, обозначаемый , состоит из следующих аффинных перестановок: ^[37]${\displaystyle \{0,\ldots ,n-1\}}$${\displaystyle J=\{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}}$${\displaystyle s_{i}}$${\displaystyle ({\widetilde {S}}_{n})_{J}}$ ${\displaystyle g\cdot ({\widetilde {S}}_{n})_{J}}$${\displaystyle ({\widetilde {S}}_{n})^{J}}$$${\displaystyle ({\widetilde {S}}_{n})^{J}=\left\{u\in {\widetilde {S}}_{n}\colon u(i-n+1)<u(i-n+2)<\cdots <u(i-1)<u(i)\right\}.}$$

В частном случае, когда , так что это стандартная копия внутри , элементы могут быть естественным образом представлены диаграммами счет : целые числа расположены в бесконечной полосе шириной n , последовательно увеличиваясь вдоль строк и затем сверху вниз; целые числа обведены кружком, если они лежат непосредственно над одним из элементов окна представителя минимального смежного класса. Например, представитель минимального смежного класса представлен диаграммой счет справа. Чтобы вычислить длину представителя из диаграммы счет, складываем количество необведенных чисел, которые меньше последнего обведенного кружком элемента в каждом столбце. (В показанном примере это дает .) ^[49]${\displaystyle J=\{s_{1},\ldots ,s_{n-1}\}}$${\displaystyle ({\widetilde {S}}_{n})_{J}\cong S_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle ({\widetilde {S}}_{n})^{J}\cong {\widetilde {S}}_{n}/S_{n}}$${\displaystyle u=[-5,0,6,9]}$${\displaystyle 5+3+0+1=9}$

Другие комбинаторные модели представителей смежных классов минимальной длины для могут быть заданы в терминах основных разбиений ( целочисленных разбиений , в которых ни одна длина крючка не делится на n ) или ограниченных разбиений (целочисленных разбиений, в которых ни одна часть не больше n − 1 ). При этих соответствиях можно показать, что слабый порядок Брюа на изоморфен определенному подмножеству решетки Юнга . ^{[50] [51]}${\displaystyle {\widetilde {S}}_{n}/S_{n}}$${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

Порядок Брюа на имеет следующую комбинаторную реализацию. Если u — аффинная перестановка, а i и j — целые числа, то определим как количество целых чисел a, таких что и . (Например, при , имеем : три соответствующих значения — , которые соответственно отображаются u в 1, 2 и 4.) Тогда для двух аффинных перестановок u , v , имеем это в порядке Брюа тогда и только тогда, когда для всех целых чисел i , j . ^[52]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle u[i,j]}$${\displaystyle a\leq i}$${\displaystyle u(a)\geq j}$${\displaystyle u=[2,0,4]\in {\widetilde {S}}_{3}}$${\displaystyle u[3,1]=3}$${\displaystyle a=0,1,3}$${\displaystyle u\leq v}$${\displaystyle u[i,j]\leq v[i,j]}$

В конечной симметрической группе соответствие Робинсона–Шенстеда дает биекцию между группой и парами стандартных таблиц Юнга одинаковой формы. Эта биекция играет центральную роль в комбинаторике и теории представлений симметрической группы . Например, на языке теории Каждана–Люстига две перестановки лежат в одной левой ячейке тогда и только тогда, когда их образы при Робинсоне–Шенстеде имеют одну и ту же таблицу Q , и в одной и той же правой ячейке тогда и только тогда, когда их образы имеют одну и ту же таблицу P. В (Shi 1986) Цзянь-И Ши показал, что левые ячейки для индексируются вместо этого таблоидами , ^[d] а в (Shi 1991) он дал алгоритм для вычисления таблоида, аналогичного таблице P для аффинной перестановки. В (Chmutov, Pylyavskyy & Yudovina 2018) авторы расширили работу Ши, чтобы дать биективное отображение между и тройками, состоящими из двух таблоидов одинаковой формы и целочисленного вектора, элементы которого удовлетворяют определенным неравенствам. Их процедура использует матричное представление аффинных перестановок и обобщает конструкцию тени , введенную в (Viennot 1977).${\displaystyle (P,Q)}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle (P,Q,\rho )}$

В некоторых ситуациях может возникнуть необходимость рассмотреть действие аффинной симметрической группы на или над альковами, обратное приведенному выше. ^[e] Эти альтернативные реализации описаны ниже.${\displaystyle \mathbb {Z} }$

В комбинаторном действии на генератор действует, переключая значения i и i + 1. В обратном действии он вместо этого переключает записи в позициях i и i + 1. Аналогично, действие общего отражения будет заключаться в переключении записей в позициях j − kn и i + kn для каждого k , фиксируя все входы в позициях, не конгруэнтных i или j по модулю n . ^{[55] [f]}${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle \mathbb {Z} }$${\displaystyle s_{i}}$

В геометрическом действии генератор действует на альков A , отражая его через одну из ограничивающих плоскостей фундаментального алькова A ₀ . В обратном действии он вместо этого отражает A через одну из своих собственных ограничивающих плоскостей. С этой точки зрения сокращенное слово соответствует обходу алькова на мозаичном пространстве V . ^[57]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle s_{i}}$

Аффинные симметрические группы тесно связаны с множеством других математических объектов.

Схема жонглирования 441, визуализированная в виде дуговой диаграммы: высота каждого броска соответствует длине дуги; два цвета узлов — это левая и правая руки жонглера. Эта схема имеет четыре пересечения, которые периодически повторяются.

В (Ehrenborg & Readdy 1996) дано соответствие между аффинными перестановками и шаблонами жонглирования, закодированными в версии нотации siteswap . ^[58] Здесь шаблон жонглирования периода n представляет собой последовательность неотрицательных целых чисел (с определенными ограничениями), которая фиксирует поведение мячей, брошенных жонглером, где число указывает продолжительность времени, в течение которого i -й бросок находится в воздухе (эквивалентно высоте броска). ^[g] Количество b мячей в шаблоне является средним . ^[60] Соответствие Эренборга–Риди сопоставляет каждому шаблону жонглирования периода n функцию, определяемую как , где индексы последовательности a берутся по модулю n . Тогда является аффинной перестановкой в ​​, и, более того, каждая аффинная перестановка возникает из шаблона жонглирования таким образом. ^[58] При этой биекции длина аффинной перестановки кодируется естественной статистикой в ​​шаблоне жонглирования: где — число пересечений (с точностью до периодичности) в дуговой диаграмме a . Это позволяет получить элементарное доказательство производящей функции для аффинных перестановок по длине. ^[61]${\displaystyle (a_{1},\ldots ,a_{n})}$${\displaystyle a_{i}}$${\displaystyle b={\frac {a_{1}+\cdots +a_{n}}{n}}}$${\displaystyle {\bf {a}}=(a_{1},\ldots ,a_{n})}$${\displaystyle w_{\bf {a}}\colon \mathbb {Z} \to \mathbb {Z} }$$${\displaystyle w_{\bf {a}}(i)=i+a_{i}-b,}$$${\displaystyle w_{\bf {a}}}$${\displaystyle {\widetilde {S}}_{n}}$$${\displaystyle \ell (w_{\bf {a}})=(b-1)n-\operatorname {cross} ({\bf {a}}),}$$${\displaystyle \operatorname {cross} ({\bf {a}})}$

Например, схема жонглирования 441 имеет и . Следовательно, она соответствует аффинной перестановке . Схема жонглирования имеет четыре пересечения, а аффинная перестановка имеет длину . ^[62]${\displaystyle n=3}$${\displaystyle b={\frac {4+4+1}{3}}=3}$${\displaystyle w_{441}=[1+4-3,2+4-3,3+1-3]=[2,3,1]}$${\displaystyle \ell (w_{441})=(3-1)\cdot 3-4=2}$

Аналогичные методы можно использовать для вывода производящей функции для представителей минимального смежного класса по длине. ^[63]${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

В конечномерном вещественном пространстве внутреннего произведения отражение — это линейное преобразование , которое фиксирует линейную гиперплоскость поточечно и отрицает вектор, ортогональный к плоскости. Это понятие может быть распространено на векторные пространства над другими полями . В частности, в комплексном пространстве внутреннего произведения отражение — это унитарное преобразование T конечного порядка, которое фиксирует гиперплоскость. ^[h] Это подразумевает, что векторы, ортогональные к гиперплоскости, являются собственными векторами T , а соответствующее собственное значение — комплексным корнем из единицы . Комплексная группа отражений — это конечная группа линейных преобразований на комплексном векторном пространстве, порожденном отражениями. ^[65]

Группы комплексных отражений были полностью классифицированы Шепардом и Тоддом (1954): каждая группа комплексных отражений изоморфна произведению неприводимых групп комплексных отражений, и каждая неприводимая либо принадлежит бесконечному семейству (где m , p , и n — положительные целые числа, такие, что p делит m ), либо является одним из 34 других (так называемых «исключительных») примеров. Группа является обобщенной симметрической группой : алгебраически это сплетение циклической группы с симметрической группой . Конкретно, элементы группы могут быть представлены мономиальными матрицами (матрицами, имеющими один ненулевой элемент в каждой строке и столбце), ненулевые элементы которых являются корнями m-й степени из единицы. Группы являются подгруппами , и в частности группа состоит из тех матриц, в которых произведение ненулевых элементов равно 1. ^[66]${\displaystyle G(m,p,n)}$${\displaystyle G(m,1,n)}$ ${\displaystyle (\mathbb {Z} /m\mathbb {Z} )\wr S_{n}}$ ${\displaystyle \mathbb {Z} /m\mathbb {Z} }$${\displaystyle S_{n}}$${\displaystyle G(m,p,n)}$${\displaystyle G(m,1,n)}$${\displaystyle G(m,m,n)}$

В (Shi 2002) Ши показал, что аффинная симметрическая группа является общим покрытием семейства в следующем смысле: для каждого положительного целого числа m существует сюръекция из в , и эти отображения совместимы с естественными сюръекциями, когда они возникают из возведения каждого элемента в степень m / p . Более того, эти проекции уважают структуру группы отражений, в том смысле, что образ каждого отражения в под является отражением в ; и аналогично, когда образ стандартного элемента Коксетера в является элементом Коксетера в . ^[67]${\displaystyle \left\{G(m,m,n)\colon m\geq 1\right\}}$${\displaystyle \pi _{m}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle G(m,m,n)}$${\displaystyle G(m,m,n)\twoheadrightarrow G(p,p,n)}$${\displaystyle p\mid m}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle \pi _{m}}$${\displaystyle G(m,m,n)}$${\displaystyle m>1}$ ${\displaystyle s_{0}\cdot s_{1}\cdots s_{n-1}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle G(m,m,n)}$

Каждая аффинная группа Кокстера связана с аффинной алгеброй Ли , определенной бесконечномерной неассоциативной алгеброй с необычайно хорошими свойствами теории представлений. ^[i] В этой ассоциации группа Кокстера возникает как группа симметрий корневого пространства алгебры Ли (двойственной подалгебре Картана ). ^[69] В классификации аффинных алгебр Ли, связанная с имеет (раскрученный) тип , с матрицей Картана для и ( циркулянтной матрицей ) для . ^[70]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle A_{n-1}^{(1)}}$ ${\displaystyle \left[{\begin{array}{rr}2&-2\\-2&2\end{array}}\right]}$${\displaystyle n=2}$$${\displaystyle \left[{\begin{array}{rrrrrr}2&-1&0&\cdots &0&-1\\-1&2&-1&\cdots &0&0\\0&-1&2&\cdots &0&0\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&0&\cdots &2&-1\\-1&0&0&\cdots &-1&2\end{array}}\right]}$$${\displaystyle n>2}$

Как и другие алгебры Каца–Муди , аффинные алгебры Ли удовлетворяют формуле характеров Вейля–Каца , которая выражает характеры алгебры через их старшие веса . ^[71] В случае аффинных алгебр Ли полученные тождества эквивалентны тождествам Макдональда . В частности, для аффинной алгебры Ли типа , связанной с аффинной симметрической группой , соответствующее тождество Макдональда эквивалентно тройному произведению Якоби . ^[72]${\displaystyle A_{1}^{(1)}}$${\displaystyle {\widetilde {S}}_{2}}$

Группы Коксетера обладают рядом специальных свойств, не свойственных всем группам. К ним относятся то, что их проблема слов разрешима (то есть существует алгоритм , который может определить, равно ли любое данное произведение генераторов элементу тождества) и то, что они являются линейными группами (то есть их можно представить группой обратимых матриц над полем). ^{[73] [74]}

Каждая группа Коксетера W связана с группой Артина–Титса , которая определяется похожим представлением, которое опускает соотношения вида для каждого генератора s . ^[75] В частности, группа Артина–Титса, связанная с , порождается n элементами, подчиняющимися соотношениям для (и никаким другим), где, как и прежде, индексы берутся по модулю n (так что ). ^[76] Предполагается, что группы Артина–Титса групп Коксетера обладают многими хорошими свойствами: например, предполагается, что они не имеют кручения , имеют тривиальный центр , имеют разрешимую проблему со словами и удовлетворяют гипотезе. Известно, что эти гипотезы не верны для всех групп Артина–Титса, но в (Charney & Peifer 2003) было показано, что обладает этими свойствами. (Впоследствии они были доказаны для групп Артина–Титса, связанных с аффинными группами Коксетера.) ^{[77] [78] [79]} В случае аффинной симметрической группы эти доказательства используют связанную структуру Гарсайда на группе Артина–Титса. ^[80]${\displaystyle B_{W}}$${\displaystyle s^{2}=1}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle \sigma _{0},\sigma _{1},\ldots ,\sigma _{n-1}}$${\displaystyle \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}}$${\displaystyle i=0,\ldots ,n-1}$${\displaystyle \sigma _{n}=\sigma _{0}}$${\displaystyle K(\pi ,1)}$${\displaystyle B_{{\widetilde {S}}_{n}}}$

Группы Артина–Титса иногда также называют обобщенными группами кос , поскольку группа Артина–Титса (конечной) симметрической группы является группой кос на n нитях. ^[81] Не все группы Артина–Титса имеют естественное представление в терминах геометрических кос. Однако группа Артина–Титса гипероктаэдрической группы (геометрически, группа симметрии n -мерного гиперкуба ; комбинаторно, группа знаковых перестановок размера n ) имеет такое представление: она задается подгруппой группы кос на нитях, состоящей из тех кос, для которых конкретная нить заканчивается в том же положении, в котором она начиналась, или, что эквивалентно, как группа кос из n нитей в кольцевой области. ^{[76] [82]} Более того, группа Артина–Титса гипероктаэдрической группы может быть записана как полупрямое произведение с бесконечной циклической группой. ^[83] Из этого следует, что можно интерпретировать как некоторую подгруппу, состоящую из геометрических кос, а также то, что это линейная группа . ^{[84] [76] [85]}${\displaystyle B_{S_{n}}}$ ${\displaystyle S_{n}^{\pm }}$${\displaystyle n+1}$${\displaystyle S_{n}^{\pm }}$${\displaystyle B_{{\widetilde {S}}_{n}}}$${\displaystyle B_{{\widetilde {S}}_{n}}}$

Аффинная симметрическая группа является подгруппой расширенной аффинной симметрической группы . Расширенная группа изоморфна сплетению . Ее элементы являются расширенными аффинными перестановками : биекциями такими, что для всех целых чисел x . В отличие от аффинной симметрической группы, расширенная аффинная симметрическая группа не является группой Кокстера . Но она имеет естественный порождающий набор, который расширяет порождающий набор Кокстера для : оператор сдвига, оконная нотация которого есть , порождает расширенную группу с простыми отражениями, при условии дополнительных соотношений . ^[15]${\displaystyle \mathbb {Z} \wr S_{n}}$${\displaystyle u\colon \mathbb {Z} \to \mathbb {Z} }$${\displaystyle u(x+n)=u(x)+n}$${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \tau }$${\displaystyle \tau =[2,3,\ldots ,n,n+1]}$${\displaystyle \tau s_{i}\tau ^{-1}=s_{i+1}}$

Геометрическое действие аффинной симметрической группы естественным образом помещает ее в семейство аффинных групп Коксетера , каждая из которых имеет аналогичное геометрическое действие на аффинном пространстве. Комбинаторное описание также может быть распространено на многие из этих групп: в Eriksson & Eriksson (1998) дано аксиоматическое описание некоторых групп перестановок, действующих на («группы Джорджа», в честь Джорджа Люстига ), и показано, что они являются в точности «классическими» группами Коксетера конечных и аффинных типов A, B, C и D. (В классификации аффинных групп Коксетера аффинная симметрическая группа имеет тип A.) Таким образом, комбинаторные интерпретации спусков, инверсий и т. д. переносятся в этих случаях. ^[86] Модели Abacus представителей смежных классов минимальной длины для параболических факторов также были распространены на этот контекст. ^[87]${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle {\widetilde {S}}_{n}}$${\displaystyle \mathbb {Z} }$

Изучение групп Коксетера в целом можно было бы назвать впервые возникшим в классификации правильных многогранников ( Платоновых тел ) в Древней Греции. Современное систематическое исследование (связывающее алгебраические и геометрические определения конечных и аффинных групп Коксетера) началось в работах Коксетера в 1930-х годах. ^[88] Комбинаторное описание аффинной симметрической группы впервые появляется в работе Люстига (1983) и было расширено Ши (1986); оба автора использовали комбинаторное описание для изучения ячеек Каждана–Люстига . ^{[89] [90]} Доказательство того, что комбинаторное определение согласуется с алгебраическим определением, было дано Эрикссоном и Эрикссоном (1998). ^[90]${\displaystyle {\widetilde {S}}_{n}}$

Эта статья была адаптирована из следующего источника по лицензии CC BY 4.0 (2021) (отчеты рецензента): Джоэл Б. Льюис (21 апреля 2021 г.), «Аффинная симметричная группа» (PDF) , WikiJournal of Science , 4 (1): 3, doi : 10.15347/WJS/2021.003 , ISSN  2470-6345, Wikidata  Q100400684

• Allcock, Daniel (2002), «Картинки кос для групп Артина», Trans. Amer. Math. Soc. , 354 (9): 3455–3474, doi : 10.1090/S0002-9947-02-02944-6 , S2CID  14473723
• Бизли, Элизабет; Николс, Маргарет; Пак, Мин Хэ; Ши, Сяо Линь; Юцис, Александр (2015), «Биективные проекции на параболические факторы аффинных групп Вейля», J. Algebr. Comb. , 41 (4): 911–948, arXiv : 1212.0771 , doi : 10.1007/s10801-014-0559-9
• Берг, Крис; Джонс, Брант; Вазирани, Моника (2009), «Биекция на основных разбиениях и параболическое фактор аффинной симметрической группы», J. Combin. Theory Ser. A , 116 (8): 1344–1360, arXiv : 0804.1380 , doi :10.1016/j.jcta.2009.03.013, S2CID  3032099
• Билли, Сара К.; Джокуш, Уильям; Стэнли, Ричард П. (1993), «Некоторые комбинаторные свойства многочленов Шуберта», J. Algebr. Comb. , 2 (4): 345–374, doi : 10.1023/A:1022419800503 , hdl : 2027.42/46173 , S2CID  8628113
• Бьёрнер, Андерс ; Бренти, Франческо (1996), «Аффинные перестановки типа А», Electron. Дж. Комбин. , 3 (2): R18, doi : 10.37236/1276 , S2CID  2987208
• Бьёрнер, Андерс ; Бренти, Франческо (2005), Комбинаторика групп Кокстера , Springer, doi : 10.1007/3-540-27596-7, ISBN 978-3540-442387, S2CID  115235335
• Кэмерон, Питер Дж. (1994), Комбинаторика: темы, методы, алгоритмы , Cambridge University Press, doi : 10.1017/CBO9780511803888, ISBN 978-0-521-45761-3, S2CID  115451799
• Чарни, Рут ; Пейфер, Дэвид (2003), « -гипотеза для аффинных бриадных групп», Comment. Math. Helv. , 78 (3): 584–600, doi : 10.1007/S00014-003-0764-Y , S2CID  54016405${\displaystyle K(\pi ,1)}$
• Чмутов, Майкл; Льюис, Джоэл Брюстер; Пилявский, Павел (2022), "Аффинное обобщение эвакуации", Selecta Math. , Новая серия, 28 (4): Статья 67, arXiv : 1706.00471 , doi : 10.1007/s00029-022-00779-x, S2CID  119168718
• Чмутов, Михаэль; Фриден, Габриэль; Ким, Донгкван; Льюис, Джоэл Брюстер; Юдовина, Елена (2022), «Монодромия в ячейках Каждана-Люстига в аффинном типе A», Math. Annalen , 386 (3–4): 1891–1949, arXiv : 1806.07429 , doi :10.1007/s00208-022-02434-4, S2CID  119669284
• Чмутов, Михаил; Пылявский, Павел; Юдовина, Елена (2018), "Матрично-шаровая конструкция аффинного соответствия Робинсона-Шенстеда", Selecta Math. , Новая серия, 24 (2): 667–750, arXiv : 1511.05861 , doi :10.1007/s00029-018-0402-6, S2CID  119086049
• Кларк, Эрик; Эренборг, Ричард (2011), «Превышение аффинных перестановок», Advances in Applied Mathematics , 46 (1–4): 175–191, doi : 10.1016/j.aam.2009.12.006 , S2CID  15349463
• Коксетер, HSM (1973), Правильные многогранники (3-е изд.), Довер, ISBN 0-486-61480-8
• Крайтс, Эндрю (2010), «Избегание перечисления шаблонов для аффинных перестановок», Electron. J. Combin. , 17 (1): R127, arXiv : 1002.1933 , doi : 10.37236/399 , S2CID  15383510
• Эренборг, Ричард ; Ридди, Маргарет (1996), «Жонглирование и приложения к q -аналогам», Discrete Math. , 157 (1–3): 107–125, CiteSeerX  10.1.1.8.6684 , doi :10.1016/S0012-365X(96)83010-X, S2CID  18149014
• Эрикссон, Хенрик; Эрикссон, Киммо (1998), «Аффинные группы Вейля как бесконечные перестановки», Electron. Дж. Комбин. , 5 : R18, doi : 10.37236/1356 , S2CID  218962
• Галлиан, Джозеф А. (2013), Современная абстрактная алгебра (8-е изд.), Brooks/Cole, ISBN 978-1-133-59970-8, LCCN  2012938179
• Грин, Р. М. (2002), «О 321-избегании перестановок в аффинных группах Вейля», J. Algebr. Comb. , 15 (3): 241–252, doi : 10.1023/A:1015012524524 , S2CID  10583938
• Hanusa, Christopher RH; Jones, Brant C. (2010), «Перечисление полностью коммутативных аффинных перестановок», Eur. J. Comb. , 31 (5): 1342–1359, arXiv : 0907.0709 , doi : 10.1016/j.ejc.2009.11.010, S2CID  789357
• Hanusa, Christopher RH; Jones, Brant C. (2012), «Модели абакуса для параболических частных аффинных групп Вейля», J. Algebra , 361 : 134–162, arXiv : 1105.5333v2 , doi : 10.1016/j.jalgebra.2012.03.029 , S2CID  47583179
• Хамфрис, Джеймс Э. (1990), Группы отражения и группы Коксетера , Cambridge University Press, doi :10.1017/CBO9780511623646, ISBN 0-521-37510-X, S2CID  121077209
• Кац, Виктор Г. (1990), Бесконечномерные алгебры Ли (PDF) (3-е изд.), Cambridge University Press, doi : 10.1017/CBO9780511626234, ISBN 0-521-46693-8
• Кейн, Ричард (2001), Группы отражений и теория инвариантов , Книги CMS по математике/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi : 10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, S2CID  119694827
• Кент, IV, Ричард П.; Пейфер, Дэвид (2002), «Геометрическое и алгебраическое описание групп кольцевых кос», Международная конференция по геометрическим и комбинаторным методам в теории групп и теории полугрупп (Линкольн, NE, 2000), Internat. J. Algebra Comput. , 12 (1–2): 85–97, doi :10.1142/S0218196702000997, S2CID  13593688
• Кнутсон, Аллен ; Лэм, Томас; Шпейер, Дэвид Э. (2013), «Позитроидные многообразия: жонглирование и геометрия», Compositio Mathematica , 149 (10): 1710–1752, arXiv : 0903.3694 , doi : 10.1112/S0010437X13007240 , S2CID  16108179
• Лэм, Томас (2015), «Форма случайного аффинного элемента группы Вейля и случайные разбиения ядра», Ann. Probab. , 43 (4): 1643–1662, arXiv : 1102.4405v3 , doi : 10.1214/14-AOP915 , S2CID  119691692
• Лапуант, Люк; Морс, Дженнифер (2005), «Таблицы на -ядрах, сокращенные слова для аффинных перестановок и -расширения Шура», J. Combin. Theory Ser. A , 112 (1): 44–81, doi : 10.1016/j.jcta.2005.01.003 , S2CID  161241${\displaystyle k+1}$${\displaystyle k}$
• Лерер, Густав И.; Тейлор, Дональд Э. (2009), Унитарные группы отражения , Серия лекций Австралийского математического общества, т. 20, Cambridge University Press , ISBN 978-0-521-74989-3, г-н  2542964
• Льюис, Джоэл Брюстер (2020), «Заметка о действии Гурвица на факторизации отражений элементов Кокстера в комплексных группах отражений», Electron. J. Combin. , 27 (2): P2.54, arXiv : 2001.08238 , doi : 10.37236/9351 , S2CID  219176795
• Льюис, Джоэл Брюстер; Маккаммонд, Джон; Петерсен, Т. Кайл; Швер, Петра (2019), «Вычисление длины отражения в аффинной группе Коксетера», Trans. Amer. Math. Soc. , 371 (6): 4097–4127, arXiv : 1710.06920 , doi : 10.1090/tran/7472, S2CID  119617021
• Льюис, Джоэл Брюстер; Райнер, Виктор (2016), «Циклические схемы и действие Гурвица в конечных корневых системах», The New York Journal of Mathematics , 22 : 1457–1486, arXiv : 1603.05969 , MR  3603073, S2CID  1789116
• Люстиг, Джордж (1983), «Некоторые примеры квадратично интегрируемых представлений полупростых p -адических групп», Trans. Amer. Math. Soc. , 277 : 623–653, doi : 10.1090/S0002-9947-1983-0694380-4 , S2CID  54190838
• Маккаммонд, Джон (2017), «Загадочная геометрия групп Артина», Winter Braids Lect. Notes , 4 (Winter Braids VII (Кан, 2017)): Exp. No. 1, 30, doi : 10.5802/wbln.17 , S2CID  128279613
• Маккаммонд, Джон; Салуэй, Роберт (2017), «Группы Артина евклидова типа», Invent. Math. , 210 (1): 231–282, arXiv : 1312.7770 , Bibcode : 2017InMat.210..231M, doi : 10.1007/s00222-017-0728-2, S2CID  253738806
• Паолини, Джованни; Сальветти, Марио (2021), «Доказательство гипотезы об аффинных группах Артина», Invent. Математика. , 224 (2): 487–572, arXiv : 1907.11795 , doi : 10.1007/s00222-020-01016-y, S2CID  253738279${\displaystyle K(\pi ,1)}$
• Петерсен, Т. Кайл (2015), Эйлеровы числа , Birkhäuser Advanced Texts Basler Lehrbücher, Birkhauser, doi : 10.1007/978-1-4939-3091-3, ISBN 978-1-4939-3090-6
• Польстер, Буркард (2003), Математика жонглирования , Springer, doi :10.1007/b98883, ISBN 0-387-95513-5, S2CID  221274895
• Райнер, Виктор (1995), "Распределение спусков и длины в группе Коксетера", Electron. J. Combin. , 2 : R25, doi : 10.37236/1219 , S2CID  6602595
• Шепард, GC ; Тодд, JA (1954), "Конечные унитарные группы отражений", Canad. J. Math. , 6 : 274–304, doi : 10.4153/CJM-1954-028-3 , S2CID  3342221
• Ши, Цзянь-И (1986), Клетки Каждана-Люстига в некоторых аффинных группах Вейля , Lecture Notes in Mathematics, т. 1179, Springer, doi : 10.1007/bfb0074968, ISBN 3-540-16439-1, S2CID  117899042
• Ши, Цзянь И (1987), «Альковы, соответствующие аффинной группе Вейля», J. London Math. Soc. , 2, 35 (1): 42–55, doi :10.1112/jlms/s2-35.1.42, S2CID  119897519
• Ши, Цзянь-И (1991), «Обобщенный алгоритм Робинсона–Шенстеда на аффинной группе Вейля типа A _{n −1} », Журнал алгебры , 139 (2): 364–394, CiteSeerX  10.1.1.551.3094 , doi :10.1016/0021-8693(91)90300-W, S2CID  124324517
• Ши, Цзянь-И (2002), «Некоторые импримитивные группы отражения и их общие версии», Trans. Amer. Math. Soc. , 354 (5): 2115–2129, doi : 10.1090/S0002-9947-02-02941-0 , S2CID  53996908
• Стембридж, Джон (1996), «О полностью коммутативных элементах групп Коксетера», J. Algebr. Comb. , 5 (4): 353–385, doi : 10.1007/BF00193185 , hdl : 2027.42/46260 , S2CID  195239538
• Вьенно, Г. (1977), «Une forme géométrique de la cordance de Robinson-Schensted», в Foata, Dominique (ed.), Combinatoire et Représentation du Groupe Symétrique , Lecture Notes in Mathematics (на французском языке), vol. 579, Springer, стр. 29–58, номер документа : 10.1007/BFb0090011, ISBN. 978-3-540-08143-2, S2CID  118727388