Октакуб (скульптура)

Octacube — это большая скульптура из нержавеющей стали , выставленная на кафедре математики Университета штата Пенсильвания в Стейт-колледже, штат Пенсильвания . Скульптура представляет собой математический объект, называемый 24-ячейкой или «октакубом». Поскольку реальная 24-ячейка является четырехмерной , произведение искусства на самом деле является проекцией в трехмерный мир.

Октакуб обладает очень высокой внутренней симметрией , которая соответствует особенностям химии ( молекулярная симметрия ) и физики ( квантовая теория поля ).

Скульптура была разработана Адрианом Окняну  [de] , профессором математики в Университете штата Пенсильвания . Механический цех университета потратил больше года на создание сложной металлоконструкции. Octacube был профинансирован выпускницей в память о ее муже Кермите Андерсоне, погибшем в результате атак 11 сентября .

Металлический скелет Octacube имеет размеры около 6 футов (1,8 метра) во всех трех измерениях. Это сложная конструкция из неокрашенных, треугольных фланцев. Основание представляет собой гранитный блок высотой 3 фута (0,91 метра) с гравировкой. ^[1]

Художественное произведение было разработано Адрианом Окняну, профессором математики из Университета штата Пенсильвания. Он предоставил спецификации для 96 треугольных деталей скульптуры из нержавеющей стали и для их сборки. Изготовление было выполнено в механическом цехе Университета штата Пенсильвания под руководством Джерри Андерсона. Работа заняла больше года, включая гибку, сварку и резку. Обсуждая конструкцию, Окняну сказал: ^[1]

Очень сложно заставить 12 стальных листов идеально и согласованно состыковаться в каждой из 23 вершин, не оставляя следов сварки. Люди, которые это построили, действительно являются экспертами и перфекционистами мирового класса — художниками по стали.

Из-за отражающего металла под разными углами внешний вид приятно странный. В некоторых случаях зеркальные поверхности создают иллюзию прозрачности, показывая отражения с неожиданных сторон конструкции. Создатель скульптуры-математик прокомментировал: ^[1]

Когда я увидел саму скульптуру, я испытал настоящий шок. Я никогда не представлял себе игру света на поверхностях. Есть тонкие оптические эффекты, которые можно почувствовать, но нельзя точно определить.

• Виды Октакюба с разных ракурсов
• 
• 
• 

Платоновы тела — это трехмерные фигуры с особой, высокой симметрией . Они являются следующим шагом по размерности после двумерных правильных многоугольников (квадратов, равносторонних треугольников и т. д.). Пять Платоновых тел — это тетраэдр (4 грани), куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней). Они были известны со времен древних греков и ценились за свою эстетическую привлекательность и философское, даже мистическое значение. (См. также диалог Платона «Тимей »).

Платоновы тела
Тетраэдр	Куб	Октаэдр	Додекаэдр	Икосаэдр

В более высоких измерениях аналогами Платоновых тел являются правильные многогранники . Эти формы были впервые описаны в середине 19 века швейцарским математиком Людвигом Шлефли . В четырех измерениях их шесть : пентахорон ( 5-ячеечный ), тессеракт ( 8-ячеечный ), гексадекахорон ( 16-ячеечный ), октакуб ( 24-ячеечный ), гекатоникосохорон ( 120-ячеечный ) и гексакосихорон ( 600-ячеечный ).

24-ячейка состоит из 24 октаэдров , соединенных в 4-мерном пространстве. Вершинная фигура 24-ячейки (трехмерная фигура, образованная при срезании четырехмерного угла) — куб. Несмотря на свое многозначительное название, октакуб не является четырехмерным аналогом ни октаэдра, ни куба. Фактически, это единственный из шести четырехмерных правильных многогранников, у которого отсутствует соответствующее Платоново тело. ^{[примечание 1]}

Попытки изобразить 24-клеточную
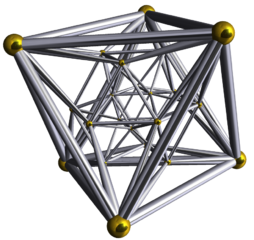Диаграмма Шлегеля	4-мерное вращение

Окняну объясняет концептуальную сложность работы в четвертом измерении: ^[1] «Хотя математики могут работать с четвертым измерением абстрактно, добавляя четвертую координату к трем, которые мы используем для описания точки в пространстве, четвертое пространственное измерение трудно визуализировать».

Хотя невозможно увидеть или создать 4-мерные объекты, их можно отобразить в более низких измерениях, чтобы получить некоторые впечатления от них. Аналогом преобразования 4-мерной 24-клеточной в ее 3-мерную скульптуру является картографическая проекция , где поверхность 3-мерной Земли (или глобуса) сводится к плоской 2-мерной плоскости (переносной карте). Это делается либо с помощью света, «отбрасывающего тень» от глобуса на карту, либо с помощью некоторого математического преобразования. Существует много различных типов картографических проекций: знакомая прямоугольная Меркатора (используется для навигации), круговая гномоническая (первая изобретенная проекция) и несколько других. Все они имеют ограничения, заключающиеся в том, что они показывают некоторые особенности искаженным образом — «нельзя расплющить апельсиновую корку, не повредив ее», — но они являются полезными наглядными пособиями и удобными справочными материалами.

Точно так же, как внешняя часть Земли представляет собой двумерную оболочку (изогнутую в третье измерение), внешняя часть 4-мерной формы представляет собой трехмерное пространство (но свернутое через гиперпространство, четвертое измерение). Однако, как поверхность земного шара не может быть отображена на плоскости без некоторых искажений, так и внешняя трехмерная форма 24-ячеечной 4-мерной гиперформы не может быть отображена на плоскости. На изображении справа 24-ячейка показана спроецированной в пространство как трехмерный объект (и тогда изображение является его двумерной визуализацией с перспективой для удобства глаза). Некоторые искажения:

• Изогнутые линии краев: они прямые в четырех измерениях, но проекция в более низкое измерение заставляет их казаться изогнутыми (аналогичные эффекты возникают при картографировании Земли).
• Из-за сложности объекта необходимо использовать полупрозрачные грани, чтобы было видно множество «коробок» (восьмигранных ячеек).
• Ясно видны только 23 ячейки. 24-я ячейка — это «снаружи внутрь», все внешнее пространство вокруг объекта, видимое в трех измерениях.

Для отображения 24-ячеечной структуры Окняну использует связанную проекцию, которую он называет оконной радиальной стереографической проекцией . Как и в стереографической проекции, в трехмерном пространстве показаны кривые линии. Вместо использования полупрозрачных поверхностей в гранях ячеек вырезаются «окна», чтобы можно было видеть внутренние ячейки. Кроме того, физически присутствуют только 23 вершины. 24-я вершина «появляется в бесконечности» из-за проекции; то, что мы видим, — это 8 ног и рук скульптуры, расходящихся наружу от центра трехмерной скульптуры. ^[1]

Скульптура Octacube имеет очень высокую симметрию. Структура из нержавеющей стали имеет ту же степень симметрии, что и куб или октаэдр. Художественное произведение можно визуализировать как связанное с кубом: руки и ноги конструкции простираются до углов. Вообразить октаэдр сложнее; для этого нужно думать о гранях визуализированного куба, образующих углы октаэдра. Куб и октаэдр имеют ту же степень и тип симметрии: октаэдрическую симметрию , называемую Oh ₍ порядок 48) в математической нотации. Некоторые, но не все, элементы симметрии

• 3 различные оси вращения четырехкратного порядка (по одной через каждую пару противоположных граней визуализированного куба): вверх/вниз, внутрь/наружу и влево/вправо, как показано на фотографии
• 4 различные тройные оси вращения (по одной через каждую пару противоположных углов куба [вдоль каждой из противоположных пар рук/ног])
• 6 различных осей вращения двойного порядка (по одной через середину каждого противоположного ребра визуализированного куба)
• 9 зеркальных плоскостей, которые делят пополам визуализированный куб
  • 3, которые разрезают его сверху/снизу, слева/справа и спереди/сзади. Эти зеркала представляют его отражательную двугранную подсимметрию D _2h , порядок 8 (подчиненная симметрия любого объекта с октаэдрической симметрией)
  • 6, которые идут вдоль диагоналей противоположных граней визуализированного куба (они идут вдоль двойных наборов пар руки-ноги). Эти зеркала представляют его отражательную тетраэдрическую подсимметрию T _d , порядок 24 (подчиненная симметрия любого объекта с октаэдрической симметрией).

Используя точки средней комнаты, скульптура представляет корневые системы типа D4, B4=C4 и F4, то есть все 4d, кроме A4. Она может визуализировать проекцию D4 на B3 и D4 на G2.

Многие молекулы имеют ту же симметрию, что и скульптура Octacube . Органическая молекула кубан (C ₈ H ₈ ) является одним из примеров. Руки и ноги скульптуры похожи на выступающие наружу атомы водорода. Гексафторид серы (или любая молекула с точной октаэдрической молекулярной геометрией ) также имеет ту же симметрию, хотя сходство не столь велико.

Молекулы с одинаковой симметрией

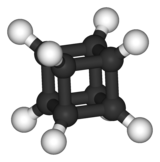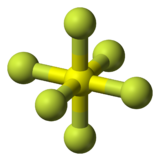Кубанский	Гексафторид серы

Octacube также показывает параллели с концепциями теоретической физики. Создатель Окняну исследует математические аспекты квантовой теории поля (КТП). Лауреат премии Филдса Эд Виттен описал эту тему как самую сложную область в физике. ^{[2] Часть работы Окняну заключается в} построении теоретических и даже физических моделей особенностей симметрии в КТП. Окняну ссылается на взаимосвязь внутренней и внешней половин структуры как на аналогичную взаимосвязи частиц со спином 1/2 (например, электронов ) и частиц со спином 1 (например, фотонов ). ^[1]

Octacube был заказан и профинансирован Джилл Андерсон, выпускницей математического факультета PSU 1965 года, в память о ее муже Кермите, еще одном выпускнике математического факультета 1965 года, который погиб в результате террористических атак 11 сентября . ^[1] Подводя итоги мемориала, Андерсон сказала: ^[1]

Я надеюсь, что скульптура побудит студентов, преподавателей, администраторов, выпускниц и друзей задуматься и оценить прекрасный мир математики. Я также надеюсь, что все, кто увидит скульптуру, начнут понимать отрезвляющий факт, что каждый уязвим к чему-то ужасному, что может случиться с ним, и что мы все должны научиться жить одним днем, извлекая максимум пользы из того, что нам дано. Было бы здорово, если бы каждый, кто увидит Octacube, ушел с чувством, что быть добрым к другим — это хороший способ жить.

Андерсон также финансировал математическую стипендию имени Кермита, в то же время, когда проект скульптуры был реализован. ^[1]

Более полное объяснение скульптуры, включая то, как она была сделана, как финансировалось ее строительство и ее роль в математике и физике , было предоставлено Университетом штата Пенсильвания. ^[1] Кроме того, Окняну предоставил свой собственный комментарий. ^[3]

Художники:

• Сальвадор Дали , художник аллюзий четвертого измерения
• Дэвид Смит , скульптор абстрактных геометрических фигур из нержавеющей стали.
• Тони Смит , еще один создатель больших абстрактных геометрических скульптур

Математика:

• Теория групп , математическая дисциплина, которая исторически охватывала большую часть исследований симметрии.
• Операторная алгебра и теория представлений , области математических исследований Окняну

Примечания

Цитаты

• Видео от Penn State о Octacube
• Пользователь создал видео о том, как представить четырехмерный объект (но тессеракт). Обратите внимание на обсуждение проекций на ~22 минуте и обсуждение ячеек в модели на ~35 минуте.

40°47′51.5″с.ш. 77°51′43.7″з.д. / 40.797639°с.ш. 77.862139°з.д. / 40.797639; -77.862139