Отношение доступности

Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Июль 2020 г. ) ( Узнайте, как и когда удалять это сообщение )

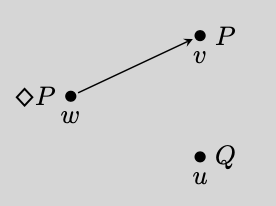
Отношение доступности — это отношение , которое играет ключевую роль в назначении значений истинности предложениям в реляционной семантике для модальной логики . В реляционной семантике значение истинности модальной формулы в возможном мире может зависеть от того, что истинно в другом возможном мире , но только если отношение доступности относится к . Например, если выполняется в некотором мире , таком что , формула будет истинна в . Этот факт имеет решающее значение. Если не относится к , то будет ложным в , если также не выполняется в некотором другом мире, таком что . ^{[1] [2]}${\displaystyle w}$${\displaystyle v}$${\displaystyle R}$${\displaystyle w}$${\displaystyle v}$${\displaystyle P}$${\displaystyle v}$${\displaystyle wRv}$${\displaystyle \Бриллиант P}$${\displaystyle w}$${\displaystyle wRv}$${\displaystyle R}$${\displaystyle w}$${\displaystyle v}$${\displaystyle \Бриллиант P}$${\displaystyle w}$${\displaystyle P}$${\displaystyle u}$${\displaystyle wRu}$

Отношения доступности концептуально мотивированы тем фактом, что модальные высказывания естественного языка зависят от некоторых, но не от всех альтернативных сценариев. Например, предложение «Может быть, идет дождь» обычно не считается истинным просто потому, что можно представить себе сценарий, в котором идет дождь. Скорее, его истинность зависит от того, исключается ли такой сценарий доступной информацией. Этот факт можно формализовать в модальной логике, выбрав отношение доступности таким образом, что если и только если оно совместимо с информацией, доступной говорящему в .${\displaystyle wRv}$${\displaystyle v}$${\displaystyle w}$

Эту идею можно распространить на различные приложения модальной логики. В эпистемологии можно использовать эпистемическое понятие доступности, где для индивидуума iff не знает чего-то, что исключало бы гипотезу, что . В деонтической модальной логике можно сказать, что iff является морально идеальным миром, учитывая моральные стандарты . При применении модальной логики к информатике так называемые возможные миры можно понимать как представление возможных состояний, а отношение доступности можно понимать как программу. Тогда iff выполнение программы может переводить компьютер из состояния в состояние .${\displaystyle wRv}$${\displaystyle Я}$${\displaystyle Я}$${\displaystyle w'=v}$${\displaystyle wRv}$${\displaystyle v}$${\displaystyle w}$${\displaystyle wRv}$${\displaystyle w}$${\displaystyle v}$

Различные применения модальной логики могут предполагать различные ограничения на допустимые отношения доступности, которые, в свою очередь, могут приводить к различным валидностям. Математическое исследование того, как валидности связаны с условиями на отношениях доступности, известно как теория модального соответствия .

• Модальная логика
• Возможные миры
• Пропозициональное отношение
• Модальная глубина

• Герла, Г.; Трансформационная семантика для логики первого порядка , Logique et Analyse, № 117–118, стр. 69–79, 1987.
• Фительсон, Брэндон; Заметки о «доступности» и модальности , 2003.
• Браун, Кертис; Пропозициональная модальная логика: несколько первых шагов , 2002.
• Крипке, Сол; Именование и необходимость , Оксфорд, 1980.
• Льюис, Дэвид К. (1968). «Теория двойников и квантифицированная модальная логика». The Journal of Philosophy . 65 (5): 113–126. doi :10.2307/2024555. JSTOR  2024555.
• Гаске, Оливье и др. (2013). Миры Крипке: Введение в модальную логику через таблицы. Springer. стр. 14–16. ISBN 978-3764385033. Получено 23 июля 2020 г. .
• Список логических систем Список большинства наиболее популярных модальных логик.