Настройка пяти пределов
Настройка с пятью пределами , настройка с пятью пределами или настройка с пятью простыми пределами (не путать с настройкой с пятью нечетными пределами ) — это любая система настройки музыкального инструмента , которая получает частоту каждой ноты путем умножения частоты заданной опорной ноты (базовой ноты) на произведения целых степеней 2, 3 или 5 ( простые числа ограничены 5 или меньше), например, 2 −3 ·3 1 ·5 1 = 15/8 .
Степени 2 представляют интервальные движения по октавам. Степени 3 представляют движения по интервалам чистых квинт (плюс одна октава, которую можно удалить, умножив на 1/2, т. е. 2 −1 ). Степени 5 представляют интервалы больших терций (плюс две октавы, удаляемые, умножив на 1/4, т. е. 2 −2 ). Таким образом, настройки 5-го предела полностью построены из наложения трех основных чисто настроенных интервалов (октавы, терции и квинты). Поскольку восприятие консонанса, по-видимому, связано с низкими числами в гармоническом ряду, а настройка 5-го предела опирается на три самых низких простых числа, настройка 5-го предела должна быть способна производить очень консонансные гармонии. Следовательно, настройка 5-го предела считается методом получения просто интонации .
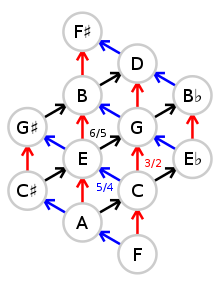
Число потенциальных интервалов, классов высоты тона, высот, ключевых центров, аккордов и модуляций, доступных для настроек с 5-ю пределами, неограниченно, поскольку никакая (ненулевая целая) степень любого простого числа не равна никакой степени любого другого простого числа, поэтому доступные интервалы можно представить себе простирающимися бесконечно в трехмерной решетке (одно измерение или одно направление для каждого простого числа). Если игнорировать октавы, то это можно рассматривать как двумерную решетку классов высоты тона (имен нот), простирающуюся бесконечно в двух направлениях.
Однако большинство систем настройки, разработанных для акустических инструментов, ограничивают общее количество тонов по практическим причинам. Также типично (но не всегда) иметь одинаковое количество тонов в каждой октаве, представляя собой октавные транспозиции фиксированного набора классов тонов. В этом случае систему настройки можно также рассматривать как октавно-повторяющуюся шкалу определенного количества тонов на октаву.
Частоту любого тона в конкретной системе настройки с 5 пределами можно получить, умножив частоту фиксированного опорного тона, выбранного для системы настройки (например, A440 , A442, A432, C256 и т. д.), на некоторую комбинацию степеней 3 и 5 для определения класса тона и некоторую степень 2 для определения октавы.
Например, если у нас есть система настройки с 5 пределами, где базовая нота — C256 (то есть она имеет 256 циклов в секунду, и мы решили назвать ее C), то f C = 256 Гц, или «частота C равна 256 Гц». Есть несколько способов определить E выше этой C. Используя терции, можно подняться на один множитель 5 и опуститься на два множителя 2, достигнув соотношения частот 5/4, или используя квинты, можно подняться на четыре множителя 3 и опуститься на шесть множителей 2, достигнув 81/64. Частоты становятся:
или
Диатоническая гамма
Если предположить, что мы ограничимся семью классами высоты тона (семью нотами на октаву), то можно настроить знакомую диатоническую гамму, используя настройку с 5-м пределом, несколькими способами, каждый из которых сделает большинство трезвучий идеально настроенными и максимально консонансными и стабильными, но оставит некоторые трезвучия в менее стабильных интервальных конфигурациях.
Выдающиеся ноты данной шкалы настроены так, что их частоты образуют соотношения относительно небольших целых чисел. Например, в тональности соль мажор соотношение частот нот соль к ре ( чистая квинта ) составляет 3/2, в то время как соль к до составляет 2/3 (нисходящая чистая квинта) или 4/3 ( чистая кварта ) по восходящей, а мажорная терция соль к си составляет 5/4.

Чистая диатоническая гамма может быть получена следующим образом. Представляя себе тональность C мажор, предположим, что мы настаиваем на том, чтобы субдоминантовый основной тон F и доминантовый основной тон G были на квинту (3:2) от тоникового основного тона C с каждой стороны, и чтобы аккорды FAC, CEG и GBD были просто мажорными трезвучиями (с частотными соотношениями 4:5:6):
| Тон | Имя | С | Д | Э | Ф | Г | А | Б | С | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Соотношение | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Естественный | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 | |||||||||
| Центы | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Шаг | Интервал | Т | т | с | Т | т | Т | с | |||||||||
| Соотношение | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Центовый шаг | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
Это известно как интенсивная диатоническая гамма Птолемея . Здесь строка, озаглавленная «Натуральная», выражает все эти отношения с помощью общего списка натуральных чисел (путем умножения строки выше на НОК ее знаменателей). Другими словами, самое низкое появление этой формы однооктавной шкалы в гармоническом ряду — это подмножество 7 из 24 гармоник, найденных в октаве от гармоник 24 до 48.
Три большие терции верны (5:4), а три малые терции соответствуют ожидаемым (6:5), но нота от ре до фа представляет собой полудитон или пифагорейскую малую терцию (равную трем нисходящим чистым квинтам, скорректированным на октаву), синтоническую комму, более узкую, чем правильно настроенная (6:5) малая терция.
В результате мы получаем шкалу, в которой EGB и ACE — это просто минорные трезвучия (10:12:15), но трезвучие DFA не имеет минорной формы или звука, которые мы могли бы ожидать, будучи (27:32:40). Более того, трезвучие BDF не является (25:30:36) уменьшенным трезвучием , которое мы получили бы, наложив две 6:5 минорных терции, а вместо этого является (45:54:64): [1] [2]
Видно, что появляются основные ступенчатые интервалы шкалы:
- с = 16:15 ( полутон )
- t = 10:9 ( минорный тон )
- T = 9:8 ( мажорный тон )
которые могут быть объединены для формирования более крупных интервалов (среди прочих):
- Ts = 6:5 (малая терция)
- Tt = 5:4 (большая терция)
- Tts = 4:3 (чистая кварта)
- TTts = 3:2 (чистая квинта)
- TTTttss 2:1 (октава)
Другой способ сделать это заключается в следующем. Думая в относительной минорной тональности A минор и используя D, A и E в качестве хребта квинт, мы можем настаивать на том, чтобы аккорды DFA, ACE и EGB были просто минорными трезвучиями (10:12:15):
| Тон | Имя | А | Б | С | Д | Э | Ф | Г | А | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Соотношение | 1/1 | 9/8 | 6/5 | 4/3 | 3/2 | 8/5 | 9/5 | 2/1 | |||||||||
| Естественный | 120 | 135 | 144 | 160 | 180 | 192 | 216 | 240 | |||||||||
| Центы | 0 | 204 | 316 | 498 | 702 | 814 | 1018 | 1200 | |||||||||
| Шаг | Интервал | Т | с | т | Т | с | Т | т | |||||||||
| Соотношение | 9/8 | 16/15 | 10/9 | 9/8 | 16/15 | 9/8 | 10/9 | ||||||||||
| Центовый шаг | 204 | 112 | 182 | 204 | 112 | 204 | 182 | ||||||||||
Если мы сравним это с предыдущей шкалой, то увидим, что для пяти пар последовательных нот соотношения ступеней остаются прежними, но для одной ноты, D, ступени CD и DE поменялись своими соотношениями.
Три больших терции по-прежнему 5:4, а три малых терции по-прежнему 6:5, а четвертая — 32:27, за исключением того, что теперь это BD вместо DF, которая составляет 32:27. FAC и CEG по-прежнему образуют только большие трезвучия (4:5:6), но GBD теперь (108:135:160), а BDF теперь (135:160:192).
Есть и другие возможности, например, повышение A вместо понижения D, но каждая корректировка нарушает что-то еще.
Очевидно, что невозможно получить все семь диатонических трезвучий в конфигурации (4:5:6) для мажора, (10:12:15) для минора и (25:30:36) для уменьшенного одновременно, если ограничиться семью тонами.
Это демонстрирует необходимость увеличения количества нот для создания желаемых гармоний в тональности.
Двенадцатитоновая гамма
Чтобы построить двенадцатитоновую гамму в пятитональной настройке, мы начнем с построения таблицы, содержащей пятнадцать правильно интонированных тонов:
| Фактор | 1 ⁄ 9 | 1 ⁄ 3 | 1 | 3 ⁄ 1 | 9 ⁄ 1 | |
|---|---|---|---|---|---|---|
| 5 ⁄ 1 | Д− 10/9 182 [3] | А 5/3 884 | Э 5/4 386 | Б 15/8 1088 | Ф ♯ + 45/32 590 [3] | соотношение центов |
| 1 | Б ♭ − 16/9 996 [3] | Ф 4/3 498 | С 1 0 | Г 3/2 702 | Д 9/8 204 | соотношение центов |
| 1 ⁄ 5 | С ♭ − 64/45 610 [3] | Д ♭ − 16/15 112 [3] | А ♭ 8/5 814 | Е ♭ 6/5 316 | В ♭ 9/5 1018 | соотношение центов |
Факторы, перечисленные в первой строке и первом столбце, являются степенями 3 и 5 соответственно (например, 1 ⁄ 9 = 3 −2 ). Цвета обозначают пары энгармонических нот с почти одинаковой высотой тона. Все соотношения выражены относительно ноты C в центре этой диаграммы (базовая нота для этой шкалы). Они вычисляются в два этапа:
- Для каждой ячейки таблицы базовое отношение получается путем умножения соответствующих множителей. Например, базовое отношение для нижней левой ячейки составляет 1/9 · 1/5 = 1/45.
- Затем базовое отношение умножается на отрицательную или положительную степень 2, настолько большую, насколько это необходимо, чтобы привести его в диапазон октавы, начинающейся с C (от 1/1 до 2/1). Например, базовое отношение для нижней левой ячейки (1/45) умножается на 2 6 , и полученное отношение равно 64/45, что является числом между 1/1 и 2/1.
Обратите внимание, что степени двойки, используемые на втором шаге, можно интерпретировать как восходящие или нисходящие октавы . Например, умножение частоты ноты на 2 6 означает ее увеличение на 6 октав. Более того, каждую строку таблицы можно считать последовательностью квинт (восходящей вправо), а каждый столбец — последовательностью больших терций (восходящей вверх). Например, в первой строке таблицы есть восходящая квинта от D и A, и еще одна (за которой следует нисходящая октава) от A до E. Это предполагает альтернативный, но эквивалентный метод вычисления тех же соотношений. Например, вы можете получить A (соотношение 5/3), начиная с C, переместив одну ячейку влево и одну вверх в таблице, что означает нисхождение на одну квинту (2/3) и восхождение на одну большую терцию (5/4):
Поскольку это ниже ноты C, вам нужно подняться на октаву выше, чтобы оказаться в желаемом диапазоне соотношений (от 1/1 до 2/1):
12-тоновая гамма получается путем удаления одной ноты для каждой пары энгармонических нот. Это можно сделать по крайней мере тремя способами, которые имеют общее удаление G ♭ , в соответствии с соглашением, действительным даже для пифагорейских гамм на основе C и 1/4-комма означает одну тональность. Обратите внимание, что это уменьшенная квинта , близкая к половине октавы, выше тонической C, которая является дисгармоничным интервалом; также ее отношение имеет самые большие значения в числителе и знаменателе всех тонов в шкале, что делает ее наименее гармоничной: все причины избегать ее.
Первая стратегия, которую мы здесь оперативно обозначаем как симметричная гамма 1 , состоит в выборе для удаления тонов в верхнем левом и нижнем правом углах таблицы. Вторая, обозначаемая как симметричная гамма 2 , состоит в отбрасывании нот в первой и последней ячейке второго ряда (обозначенного " 1 "). Третий, обозначенный как асимметричная гамма , состоит из отбрасывания первого столбца (обозначенного как " 1/9 "). Полученные 12-тоновые гаммы показаны ниже:
| Симметричная шкала 1 | ||||||
|---|---|---|---|---|---|---|
| Фактор | 1 ⁄ 9 | 1 ⁄ 3 | 1 | 3 | 9 | |
| 5 | А 5/3 | Э 5/4 | Б 15/8 | Ф ♯ + 45/32 | ||
| 1 | Б ♭ − 16/9 | Ф 4/3 | С 1 | Г 3/2 | Д 9/8 | |
| 1 ⁄ 5 | Д ♭ − 16/15 | А ♭ 8/5 | Э ♭ 6/5 | |||
| Симметричная шкала 2 | ||||||
|---|---|---|---|---|---|---|
| Фактор | 1 ⁄ 9 | 1 ⁄ 3 | 1 | 3 | 9 | |
| 5 | Д− 10/9 | А 5/3 | Э 5/4 | Б 15/8 | Ф ♯ + 45/32 | |
| 1 | Ф 4/3 | С 1 | Г 3/2 | |||
| 1 ⁄ 5 | Д ♭ − 16/15 | А ♭ 8/5 | Э ♭ 6/5 | Б ♭ 9/5 | ||
| Асимметричный масштаб | ||||||
|---|---|---|---|---|---|---|
| Фактор | 1 ⁄ 9 | 1 ⁄ 3 | 1 | 3 | 9 | |
| 5 | А 5/3 | Э 5/4 | Б 15/8 | Ф ♯ + 45/32 | ||
| 1 | Ф 4/3 | С 1 | Г 3/2 | Д 9/8 | ||
| 1 ⁄ 5 | Д ♭ − 16/15 | А ♭ 8/5 | Э ♭ 6/5 | Б ♭ 9/5 | ||
В первой и второй гамме B ♭ и D являются точной инверсией друг друга. Это не относится к третьей. Вот почему эти две гаммы считаются симметричными (хотя удаление G ♭ делает все 12 тоновых гамм, включая те, которые получены с помощью любой другой системы настройки, слегка асимметричными).
Асимметричная система имеет преимущество в том, что имеет "самые справедливые" соотношения (содержащие меньшие числа), девять чистых квинт (множитель 3/2), восемь чистых больших терций (множитель 5/4) по замыслу, но также шесть чистых малых терций (множитель 6/5). Однако она также содержит две нечистые квинты (например, D в A составляет 40/27, а не 3/2) и три нечистые малые терции (например, D в F составляет 32/27, а не 6/5), что фактически ограничивает модуляцию узким диапазоном тональностей. Аккорды тоники C, доминанты G и субдоминанты F являются чистыми, как и D ♭ , A ♭ , E ♭ и минорные аккорды Fm, Cm, Gm, Am, Bm и Em, но не Dm.
Недостатком асимметричной системы является то, что она создает 14 интервалов Вольфа , а не 12, как симметричная.
B ♭ в первой симметричной гамме отличается от B ♭ в других гаммах синтонической коммой , которая составляет более 21 цента. В равномерно темперированных гаммах разница устраняется путем придания всем ступеням одинакового соотношения частот.

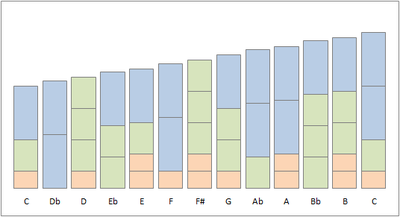 |
Построение асимметричной шкалы графически показано на рисунке. Каждый блок имеет высоту в центах конструктивных частотных соотношений 2/1, 3/2 и 5/4. Можно распознать повторяющиеся закономерности. Например, много раз следующая нота создается путем замены блока 5/4 и блока 3/2 на блок 2/1, что представляет собой соотношение 16/15.
Аналогичное изображение, построенное с использованием частотных коэффициентов 2, 3 и 5, а не 2/1, 3/2 и 5/4, можно посмотреть здесь .
Справедливые соотношения
Справедливые соотношения, используемые для построения этих гамм, могут использоваться в качестве справочного материала для оценки консонанса интервалов в других гаммах (например, см. эту сравнительную таблицу ). Однако настройка 5-го предела — не единственный метод получения справедливой интонации . Можно построить справедливые интервалы с еще более «справедливыми» соотношениями или, поочередно, со значениями, близкими к эквивалентам равномерно темперированного строя. Например, настройка 7-го предела иногда используется для получения немного более справедливого и, следовательно, более справедливого интервала для малой септимы (7/4) и ее обращения, большой секунды (8/7). Список этих справочных соотношений, которые можно назвать чистыми или строго справедливыми интервалами или соотношениями, приведен ниже:
| Название интервала | Короткий | Количество полутонов | 5-ти предельная настройка | настройка 7-ми пределов | настройка 17-предела | |||
|---|---|---|---|---|---|---|---|---|
| Симметричные весы | Асимметричные весы | |||||||
| № 1 | № 2 | Стандарт | Расширенный | |||||
| Идеальный унисон | П1 | 0 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 |
| Малая секунда | м2 | 1 | 16/15 | 16/15 | 16/15 | 16/15 | 15/14 | 14/13 |
| Главный второй | М2 | 2 | 9/8 | 10/9 | 9/8 | 9/8 | 8/7 | 8/7 |
| Малая терция | м3 | 3 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 |
| Большая терция | М3 | 4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 |
| Идеальная четвертая | П4 | 5 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 |
| Расширенная четвертая | А4 | 6 | 45/32 | 45/32 | 45/32 | 25/18 | 7/5 | 7/5 или 17/12 |
| Уменьшенная пятая | д5 | 6 | 64/45 | 64/45 | 64/45 | 36/25 | 10/7 | 10/7 или 24/17 |
| Чистая квинта | П5 | 7 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 |
| Малая секста | м6 | 8 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 |
| Большая секста | М6 | 9 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 |
| Малая септаккорда | м7 | 10 | 16/9 | 9/5 | 9/5 | 9/5 | 7/4 | 7/4 |
| Большая септаккорда | М7 | 11 | 15/8 | 15/8 | 15/8 | 15/8 | 15/8 | 13/7 |
| Чистая октава | П8 | 12 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 |
Ячейки, выделенные желтым цветом, указывают на интервалы, которые являются более четкими, чем в неокрашенных ячейках в той же строке. Те, что выделены голубым цветом, указывают на еще более четкие соотношения.
Обратите внимание, что соотношения 45/32 и 64/45 для тритонов (увеличенная кварта и уменьшенная квинта) не во всех контекстах считаются строго справедливыми, но они являются наиболее справедливыми из возможных в вышеупомянутых шкалах настройки 5-пределов. Расширенная асимметричная шкала 5-пределов (см. ниже) обеспечивает немного более справедливые соотношения для обоих тритонов (25/18 и 36/25), чистота которых также является спорной. Настройка 7-пределов допускает наиболее справедливые возможные соотношения, а именно 7/5 (около 582,512 центов, также известная как септимальный тритон ) и 10/7 (около 617,488 центов). Эти соотношения более консонантны, чем 17/12 (около 603 000 центов) и 24/17 (около 597 000 центов), которые можно получить при настройке на 17 пределов, однако последние также довольно распространены, поскольку они ближе к равномерно темперированному значению в 600 000 центов.
Вышеупомянутый интервал 7/4 (около 968,826 центов), также известный как септимальная малая септима , или гармоническая септима, был спорным вопросом на протяжении всей истории музыкальной теории; он на 31 цент ниже равномерно темперированной малой септимы.
Размер интервалов

Таблицы выше показывают только частотные соотношения каждой ноты по отношению к базовой ноте. Однако интервалы могут начинаться с любой ноты, и поэтому для каждого типа интервала можно определить двенадцать интервалов – двенадцать унисон, двенадцать полутонов , двенадцать интервалов по 2 полутона и т. д.
В настройке 5-limit каждый тип интервала, за исключением унисон и октав, имеет три или четыре различных размера. Это цена, которую приходится платить за поиск только интонации. Таблица справа показывает их частотные соотношения для асимметричной шкалы, с отклонениями, выделенными цветом, и отклонениями, соответствующими интервалам вольфа, фиолетовым цветом. Отклонения возникают, поскольку ноты определяют четыре различных полутона :
-
(«Просто» увеличенный унисон между E ♭ и E) -
(Увеличенный унисон между D ♭ и D) -
(«Всего лишь» малая секунда между C и D ♭ ) -
(Малая секунда между A и B ♭ )
Напротив, в равномерно темперированной хроматической гамме все полутоны измеряются
и интервалы любого типа имеют одинаковый размер, но ни один из них не настроен правильно, за исключением унисон и октав.
Запятые
В других системах настройки комма может быть определена как минутный интервал, равный разнице между двумя видами полутонов (диатоническим и хроматическим, также известным как малая секунда, m2 , или увеличенный унисон, A1 ). В этом случае, однако, производятся 4 вида полутонов (два A1, S 1 и S 2 , и два m2, S 3 и S 4 ) и 12 различных комм могут быть определены как разности между их размерами в центах, или, что эквивалентно, как отношения между их отношениями. Среди них мы выбираем шесть восходящих (те, у которых отношение больше 1/1, и положительный размер в центах):
| Имя запятой | Эквивалентные определения | Размер | ||
|---|---|---|---|---|
| В среднем темпераменте | В 5-ти предельном строе (асимметричный строй) | Соотношение | Центы | |
| Диасхизма ( ДС ) | в 1/6-запятая означала один | |||
| Синтоническая запятая ( SC ) | ||||
| Малый диезис ( LD ) | в 1/4-запятая означала один | |||
| Большой диезис ( GD ) | в 1/3-запятая означала один | |||
Остальные шесть соотношений отбрасываются, поскольку они являются полной противоположностью этим, и, следовательно, имеют точно такую же длину, но противоположное направление (т. е. нисходящее направление, соотношение меньше 1/1 и отрицательный размер в центах). Мы получаем запятые четырех разных размеров: диасхизма, малый диезис, синтоническая запятая и большой диезис. Поскольку S 1 ( только A1 ) и S 3 ( только m2 ) являются наиболее часто встречающимися полутонами в этой 12-тоновой шкале (см. таблицы выше), малый диезис, определяемый как соотношение между ними, является наиболее часто встречающейся запятой.
Синтоническая комма также определяется в настройке 5-limit как соотношение между мажорным тоном (M2 с размером 9/8) и минорным тоном (M2 с размером 10/9). Обратите внимание, что в других системах настройки ее нельзя определить как соотношение между диатоническими и хроматическими полутонами (m2/A1), но это важное справочное значение, используемое для настройки чистой квинты в любой системе настройки в континууме синтонической темперации (включая также мезонинные темперации).
Уменьшенные секунды
Три из вышеупомянутых комм, а именно диасхизма, диезис и большой диезис, соответствуют определению уменьшенной секунды , представляя собой разницу между размерами в центах диатонического и хроматического полутона (или, что то же самое, соотношение между их частотными отношениями).
Напротив, синтоническая комма определяется либо как разница в центах между двумя хроматическими полутонами (S 2 и S 1 ), либо между двумя диатоническими полутонами (S 4 и S 3 ), и не может считаться уменьшенной секундой.
Расширение двенадцатитоновой шкалы
В приведенной выше таблице для построения базовых соотношений используются только низкие степени чисел 3 и 5. Однако ее можно легко расширить, используя более высокие положительные и отрицательные степени тех же чисел, например, 5 2 = 25, 5 −2 = 1/25, 3 3 = 27 или 3 −3 = 1/27. Шкала с 25, 35 или даже большим количеством тонов может быть получена путем объединения этих базовых соотношений.
Например, можно получить 35 шагов, добавляя ряды в каждом направлении следующим образом:
| Фактор | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 125 | соотношение центов | А ♯ 125/72 955,0 [3] | Е ♯ 125/96 457.0 | В ♯ 125/64 1158.9 | Ф + + 375/256 660,9 [3] | С + + 1125/1024 162,9 [3] |
| 25 | соотношение центов | Ф ♯ 25/18 568,7 [3] | С ♯ 25/24 70,7 | Соль ♯ 25/16 772,6 | Д ♯ 75/64 274,6 | А ♯ + 225/128 976,5 [3] |
| 5 | соотношение центов | Д− 10/9 182,4 | А 5/3 884,4 | Е 5/4 386.3 | Б 15/8 1088.3 | Ф ♯ + 45/32 590,2 |
| 1 | соотношение центов | Б ♭ − 16/9 996,1 | Ф 4/3 498,0 | С 1/1 0,0 | Г 3/2 702,0 | Д 9/8 203,9 |
| 1/5 | соотношение центов | С ♭ − 64/45 609,8 | Д ♭ − 16/15 111,7 | А ♭ 8/5 813,7 | Е ♭ 6/5 315.6 | В ♭ 9/5 1017.6 |
| 1/25 | соотношение центов | Э − − 256/225 223,5 [3] | Б − − 128/75 925,4 [3] | Ф ♭ 32/25 427,4 | С ♭ 48/25 1129,3 | С ♭ 36/25 631,3 |
| 1/125 | соотношение центов | С − − 2048/1125 1037,1 [3] | Г − − 512/375 539,1 [3] | Д − − 128/125 41,1 [3] | А 192/125 743,0 | Э 144/125 245,0 |
Левая колонка ( 1/9 ) иногда удаляется (как в асимметричной шкале, показанной выше), тем самым создавая асимметричную таблицу с меньшим количеством тонов. Обратите внимание, что более точное соотношение получается для уменьшенной квинты (CG ♭ = 36/25) по отношению к ограниченной настройке 5-го предела, описанной выше (где C к G ♭ - = 64/45). [4]
История
В пифагорейской настройке, возможно, первой системе настройки, теоретически разработанной на Западе, [5] единственными высококонсонантными интервалами были чистая квинта и ее обращение, чистая кварта . Пифагорейская большая терция (81:64) и малая терция (32:27) были диссонантными , и это мешало музыкантам использовать трезвучия и аккорды , заставляя их на протяжении столетий писать музыку с относительно простой текстурой . В позднем Средневековье музыканты поняли, что, слегка смягчив высоту некоторых нот, пифагорейские терции можно сделать консонантными . Например, если вы уменьшите на синтоническую комму (81:80), частота E, CE (большая терция) и EG (малая терция) станет справедливой. А именно, CE сужается до справедливо интонированного соотношения
и в то же время EG расширяется до справедливого соотношения
Недостатком является то, что квинты AE и EB, сглаживая E, становятся почти такими же диссонансными, как пифагорейская волчья квинта . Но квинта CG остается консонантной, поскольку сглаживается только E (CE * EG = 5/4 * 6/5 = 3/2), и может использоваться вместе с CE для получения трезвучия C- мажор (CEG).
Обобщив это простое обоснование, Джозеффо Царлино в конце шестнадцатого века создал первую правильно интонированную 7-тоновую ( диатоническую ) гамму, которая содержала чистые чистые квинты (3:2), чистые большие терции и чистые малые терции:
Ф → А → С → Д → Г → Б → Г
Это последовательность только больших терций (M3, соотношение 5:4) и только малых терций (m3, соотношение 6:5), начинающаяся с F:
Ф + М3 + м3 + М3 + м3 + М3 + м3
Так как M3 + m3 = P5 (чистая квинта), то есть 5/4 * 6/5 = 3/2, это в точности эквивалентно диатонической гамме, полученной в 5-тоновой интонации, и, следовательно, может рассматриваться как подмножество таблицы построения, используемой для 12-тоновой ( хроматической ) гаммы:
| А | → | Э | → | Б | ||
| ↑ | ↑ | ↑ | ||||
| Ф | → | С | → | Г | → | Д |
где обе строки представляют собой последовательности только квинт, а FA, CE, GB представляют собой только большие терции:
| М3 | М3 | М3 | ||||
| + | + | + | ||||
| Ф | + | П5 | + | П5 | + | П5 |
Смотрите также
- Математика музыкальных гамм
- Микротональная музыка
- Микротюнер
- Пифагоров интервал
- Полутон
- Список интервалов в 5-ти нотной системе с интонацией
- Список средних интервалов
- Список музыкальных интервалов
- Список интервалов высоты тона
- Целотонная гамма
- Регулярный номер
- Гексани
- Электронный тюнер
- Консонанс и диссонанс
Примечания
- ^ Райт, Дэвид (2009). Математика и музыка , стр. 140–141. ISBN 978-0-8218-4873-9 .
- ^ Джонстон, Бен и Гилмор, Боб (2006). «Система нотации для расширенной простой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , стр. 78. ISBN 978-0-252-03098-7 .
- ^ abcdefghijklmno Джон Фонвилл . «Расширенная точная интонация Бена Джонстона — руководство для интерпретаторов», стр. 113–114, Perspectives of New Music , т. 29, № 2 (лето 1991 г.), стр. 106–137.
- ^ Ноты от G ♯ до D ♭ взяты из Don Michael Randel , The Harvard Dictionary of Music , 4-е издание. Кембридж, Массачусетс: Belknap Press, 2003, стр. 415. Кроме того, что касается нот от F
 В энциклопедии микротональной теории музыки Tonalsoft говорится: «На самом деле эта структура идеально описывает чисто интонационную структуру Салинаса» .
В энциклопедии микротональной теории музыки Tonalsoft говорится: «На самом деле эта структура идеально описывает чисто интонационную структуру Салинаса» . - ^ Древнейшее известное описание пифагорейской системы настройки встречается в вавилонских артефактах. См.: West, ML "The Babylonian Musical Notation and the Hurrian Melodic Texts", Music & Letters , т. 75, № 2 (май 1994 г.). стр. 161–179.
Внешние ссылки
- Искусство Штатов: микротональные/чисто интонационные произведения, написанные американскими композиторами.
- Фонд Chrysalis – Просто интонация: два определения
- Гитара Just Intonation Данте Розати 21 Tone
- Просто интонация Марка Новицки
- Просто интонация, объясненная Кайлом Ганном
- Подборка работ Just Intonation, отредактированная сетью Just Intonation Network, опубликована в архиве проекта Tellus Audio Cassette Magazine на UbuWeb
- Фонд средневековой музыки и искусств
- Music Novatory – Just Intonation Архивировано 15.06.2011 на Wayback Machine
- Почему Just Intonation звучит так хорошо?
- Архивы Уилсона
- Барбьери, Патрицио. Энгармонические инструменты и музыка, 1470–1900. (2008) Латина, Иль Леванте
- Программное обеспечение для клавиатуры Just Intonation на 22 ноты с 12 звуками индийских инструментов Libreria Editrice
- Plainsound Music Edition – Просто интонация (JI) музыка и исследования, информация о нотной записи Гельмгольца - Эллиса JI








![{\displaystyle S_{E}={\sqrt[{12}]{2}}=100.000{\text{ центов}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50bf0d2901461be5393a3b513729b1a5a0d84c9)

















