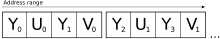YCbCr

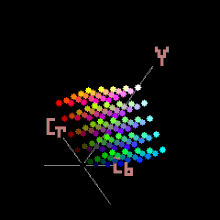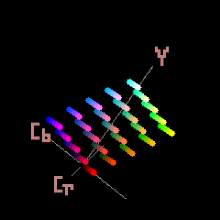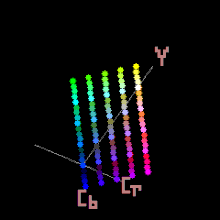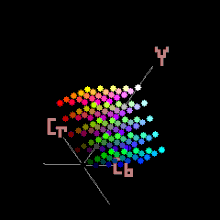
YCbCr , Y′CbCr или Y Pb/Cb Pr/Cr , также обозначаемое как YC _B C _R или Y′C _B C _R , — это семейство цветовых пространств, используемых как часть конвейера цветного изображения в системах цифрового видео и фотографии .

Y′ — это компонент яркости , а C _B и C _R — это компоненты цветности синего и красного цветов . Яркость Y′ (со штрихом ) отличается от яркости Y, что означает, что интенсивность света нелинейно кодируется на основе гамма-скорректированных основных цветов RGB .

Цветовые пространства Y′CbCr определяются математическим преобразованием координат из связанных основных цветов RGB и белой точки . Если базовое цветовое пространство RGB является абсолютным, цветовое пространство Y′CbCr также является абсолютным цветовым пространством ; и наоборот, если пространство RGB определено неточно, то и Y′CbCr тоже является абсолютным цветовым пространством. Преобразование определяется в уравнениях 32, 33 в ITU-T H.273. ^[1]

Черно-белое телевидение широко использовалось до появления цветного телевидения. Из-за большого количества существующих телевизоров и камер для новых цветных трансляций требовалась некоторая форма обратной совместимости . Французский инженер Жорж Валенси разработал и запатентовал систему передачи цвета RGB в виде сигналов яркости и цветности в 1938 году. Это позволило бы существующим черно-белым телевизорам обрабатывать только информацию о яркости и игнорировать цветность, по сути упаковывая черно-белое видео в цветное видео. Из-за этой обратной совместимости система, основанная на идее Валенси, была названа совместимым цветом . Таким же образом черно-белая трансляция могла приниматься цветным телевизором без каких-либо дополнительных схем обработки. Чтобы сохранить существующие распределения частот вещания, новой информации о цветности была предоставлена ​​​​более низкая полоса пропускания, чем информации о яркости. Это возможно, потому что люди более чувствительны к черно-белой информации (см. пример изображения справа). Это называется субдискретизацией цветности .

YCbCr и Y′CbCr являются практическим приближением к обработке цвета и перцептивной однородности, где основные цвета, примерно соответствующие красному, зеленому и синему, обрабатываются в перцептивно значимую информацию. Благодаря этому последующая обработка изображений/видео, передача и хранение могут выполнять операции и вносить ошибки перцептивно значимыми способами. Y′CbCr используется для разделения сигнала яркости (Y′), который может храниться с высоким разрешением или передаваться с высокой пропускной способностью, и двух компонентов цветности (C _B и C _R ), которые могут быть уменьшены по полосе пропускания, подвергнуты субдискретизации, сжаты или иным образом обработаны отдельно для повышения эффективности системы.

YCbCr иногда сокращается до YCC . Обычно термины Y′CbCr, YCbCr, YPbPr и YUV используются взаимозаменяемо, что приводит к некоторой путанице. Основное отличие заключается в том, что YPbPr используется с аналоговыми изображениями, а YCbCr — с цифровыми, что приводит к разным значениям масштабирования для U _max и V _max (в YCbCr оба равны ) при преобразовании в/из YUV. Y′CbCr и YCbCr различаются из-за того, скорректированы ли значения гамма-коррекцией или нет. ${\displaystyle {\tfrac {1}{2}}}$

Приведенные ниже уравнения дают более четкое представление об общих принципах и основных различиях между этими форматами.

Сигналы Y′CbCr (до масштабирования и смещения для перевода сигналов в цифровую форму) называются YPbPr и создаются из соответствующего источника RGB (красный, зеленый и синий) с гамма-коррекцией с использованием трех определенных констант KR _, KG _и KB _{следующим} образом:

${\displaystyle {\begin{align}Y'&=K_{R}\cdot R'+K_{G}\cdot G'+K_{B}\cdot B'\\P_{B}&={\frac {1}{2}}\cdot {\frac {B'-Y'}{1-K_{B}}}\\P_{R}&={\frac {1}{2}}\cdot {\frac {R'-Y'}{1-K_{R}}}\end{align}}}$

где K _R , K _G и K _B обычно выводятся из определения соответствующего пространства RGB и должны удовлетворять . ${\displaystyle K_{R}+K_{G}+K_{B}=1}$

Эквивалентную матричную манипуляцию часто называют «цветовой матрицей»:

${\displaystyle {\begin{bmatrix}Y'\\P_{B}\\P_{R}\end{bmatrix}}={\begin{bmatrix}K_{R}&K_{G}&K_{B}\\-{\frac {1}{2}}\cdot {\frac {K_{R}}{1-K_{B}}}&-{\frac {1}{2}}\cdot {\frac {K_{G}}{1-K_{B}}}&{\frac {1}{2}}\\{\frac {1}{2}}&-{\frac {1}{2}}\cdot {\frac {K_{G}}{1-K_{R}}}&-{\frac {1}{2}}\cdot {\frac {K_{B}}{1-K_{R}}}\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}}$

И обратное:

${\displaystyle {\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}={\begin{bmatrix}1&0&2-2\cdot K_{R}\\1&-{\frac {K_{B}}{K_{G}}}\cdot (2-2\cdot K_{B})&-{\frac {K_{R}}{K_{G}}}\cdot (2-2\cdot K_{R})\\1&2-2\cdot K_{B}&0\end{bmatrix}}{\begin{bmatrix}Y'\\P_{B}\\P_{R}\end{bmatrix}}}$

Здесь символы штриха (′) означают, что используется гамма-коррекция ; таким образом, R′, G′ и B′ номинально находятся в диапазоне от 0 до 1, где 0 представляет минимальную интенсивность (например, для отображения черного цвета), а 1 — максимальную (например, для отображения белого цвета ). Результирующее значение яркости (Y) будет тогда иметь номинальный диапазон от 0 до 1, а значения цветности (P _B и P _R ) будут иметь номинальный диапазон от -0,5 до +0,5. Обратный процесс преобразования можно легко получить, инвертировав приведенные выше уравнения.

При представлении сигналов в цифровой форме результаты масштабируются и округляются, и обычно добавляются смещения. Например, масштабирование и смещение, применяемые к компоненту Y′ согласно спецификации (например, MPEG-2 ^[2] ), приводят к значению 16 для черного и значению 235 для белого при использовании 8-битного представления. Стандарт имеет 8-битные оцифрованные версии C _B и C _R, масштабированные до другого диапазона от 16 до 240. Следовательно, при выполнении цветовой матрицы или обработки в пространстве YCbCr иногда требуется перемасштабирование на дробь (235-16)/(240-16) = 219/224, что приводит к искажениям квантования, когда последующая обработка не выполняется с использованием более высокой битовой глубины.

Масштабирование, которое приводит к использованию меньшего диапазона цифровых значений, чем тот, который может показаться желательным для представления номинального диапазона входных данных, допускает некоторые "перерегулирования" и "недорегулирования" во время обработки без необходимости нежелательного отсечения . Этот " headroom " и "toeroom" ^[3] также может быть использован для расширения номинальной цветовой гаммы , как указано в xvYCC .

Значение 235 обеспечивает максимальный выброс (255 - 235) / (235 - 16) = 9,1%, что немного больше теоретического максимального выброса ( феномен Гиббса ) около 8,9% от максимального (черно-белого) шага. Toeroom меньше, допуская только 16 / 219 = 7,3% выброса, что меньше теоретического максимального выброса 8,9%. Кроме того, поскольку значения 0 и 255 зарезервированы в HDMI, фактически room немного меньше.

Поскольку уравнения, определяющие Y′CbCr, сформированы таким образом, что вращают весь номинальный цветовой куб RGB и масштабируют его для вписывания в (больший) цветовой куб YCbCr, есть некоторые точки внутри цветового куба Y′CbCr, которые не могут быть представлены в соответствующей области RGB (по крайней мере, не в номинальном диапазоне RGB). Это вызывает некоторые трудности в определении того, как правильно интерпретировать и отображать некоторые сигналы Y′CbCr. Эти выходящие за пределы диапазона значения Y′CbCr используются xvYCC для кодирования цветов за пределами гаммы BT.709.

Форма Y′CbCr, которая была определена для использования в телевидении стандартной четкости в стандарте ITU-R BT.601 (ранее CCIR 601 ) для использования с цифровым компонентным видео , получена из соответствующего пространства RGB (основные цвета ITU-R BT.470-6 System M) следующим образом:

${\displaystyle {\begin{align}K_{R}&=0,299\\K_{G}&=0,587\\K_{B}&=0,114\end{align}}}$

Из приведенных выше констант и формул можно вывести следующее для ITU-R BT.601.

Аналоговый YPbPr из аналогового R'G'B' выводится следующим образом:

${\displaystyle {\begin{aligned}Y'&=&0.299\cdot R'&+&0.587\cdot G'&+&0.114\cdot B'\\P_{B}&=-&0.168736\cdot R'&-&0.331264\cdot G'&+&0.5\cdot B'\\P_{R}&=&0.5\cdot R'&-&0.418688\cdot G'&-&0.081312\cdot B'\end{aligned}}}$

Цифровой Y'CbCr (8 бит на выборку) получается из аналогового R'G'B' следующим образом:

${\displaystyle {\begin{aligned}Y'&=&16&+&(65.481\cdot R'&+&128.553\cdot G'&+&24.966\cdot B')\\C_{B}&=&128&+&(-37.797\cdot R'&-&74.203\cdot G'&+&112.0\cdot B')\\C_{R}&=&128&+&(112.0\cdot R'&-&93.786\cdot G'&-&18.214\cdot B')\end{aligned}}}$

или просто покомпонентно

${\displaystyle {\begin{aligned}(Y',C_{B},C_{R})&=&(16,128,128)+(219\cdot Y,224\cdot P_{B},224\cdot P_{R})\\\end{aligned}}}$

Результирующие сигналы находятся в диапазоне от 16 до 235 для Y′ (Cb и Cr находятся в диапазоне от 16 до 240); значения от 0 до 15 называются footroom , а значения от 236 до 255 называются headroom . Те же диапазоны квантования, отличающиеся для Y и Cb, Cr, также применяются к BT.2020 и BT.709.

В качестве альтернативы цифровой Y′CbCr может быть получен из цифрового R'dG'dB'd (8 бит на выборку, каждая из которых использует полный диапазон, где ноль представляет черный цвет, а 255 представляет белый цвет) в соответствии со следующими уравнениями:

${\displaystyle {\begin{aligned}Y'&=&16&+&{\frac {65.481\cdot R'_{D}}{255}}&+&{\frac {128.553\cdot G'_{D}}{255}}&+&{\frac {24.966\cdot B'_{D}}{255}}\\C_{B}&=&128&-&{\frac {37.797\cdot R'_{D}}{255}}&-&{\frac {74.203\cdot G'_{D}}{255}}&+&{\frac {112.0\cdot B'_{D}}{255}}\\C_{R}&=&128&+&{\frac {112.0\cdot R'_{D}}{255}}&-&{\frac {93.786\cdot G'_{D}}{255}}&-&{\frac {18.214\cdot B'_{D}}{255}}\end{aligned}}}$

В приведенной ниже формуле коэффициенты масштабирования умножаются на . Это позволяет получить значение 256 в знаменателе, которое можно вычислить одним битовым сдвигом .${\displaystyle {\frac {256}{255}}}$

${\displaystyle {\begin{aligned}Y'&=&16&+&{\frac {65.738\cdot R'_{D}}{256}}&+&{\frac {129.057\cdot G'_{D}}{256}}&+&{\frac {25.064\cdot B'_{D}}{256}}\\C_{B}&=&128&-&{\frac {37.945\cdot R'_{D}}{256}}&-&{\frac {74.494\cdot G'_{D}}{256}}&+&{\frac {112.439\cdot B'_{D}}{256}}\\C_{R}&=&128&+&{\frac {112.439\cdot R'_{D}}{256}}&-&{\frac {94.154\cdot G'_{D}}{256}}&-&{\frac {18.285\cdot B'_{D}}{256}}\end{aligned}}}$

Если цифровой источник R'd G'd B'd включает в себя пространство для ног и пространство для головы, то сначала из каждого сигнала необходимо вычесть смещение пространства для ног 16, а в уравнения необходимо включить масштабный коэффициент.${\displaystyle {\frac {255}{219}}}$

Обратное преобразование:

${\displaystyle {\begin{aligned}R'_{D}&=&{\frac {298.082\cdot Y'}{256}}&&&+&{\frac {408.583\cdot C_{R}}{256}}&-&222.921\\G'_{D}&=&{\frac {298.082\cdot Y'}{256}}&-&{\frac {100.291\cdot C_{B}}{256}}&-&{\frac {208.120\cdot C_{R}}{256}}&+&135.576\\B'_{D}&=&{\frac {298.082\cdot Y'}{256}}&+&{\frac {516.412\cdot C_{B}}{256}}&&&-&276.836\end{aligned}}}$

Обратное преобразование без округлений (с использованием значений, взятых непосредственно из рекомендации ITU-R BT.601):

${\displaystyle {\begin{aligned}R'_{D}={\frac {255}{219}}\cdot (Y'-16)&&&&&&&+{\frac {255}{224}}\cdot 1.402\cdot (C_{R}-128)\\G'_{D}={\frac {255}{219}}\cdot (Y'-16)&-&{\frac {255}{224}}\cdot 1.772&&\cdot {\frac {0.114}{0.587}}&&\cdot (C_{B}-128)&-{\frac {255}{224}}\cdot 1.402\cdot {\frac {0.299}{0.587}}\cdot (C_{R}-128)\\B'_{D}={\frac {255}{219}}\cdot (Y'-16)&+&{\frac {255}{224}}\cdot 1.772&&&&\cdot (C_{B}-128)\end{aligned}}}$

Эта форма Y′CbCr используется в основном для старых систем телевидения стандартной четкости , поскольку она использует модель RGB, которая соответствует характеристикам излучения люминофора старых ЭЛТ.

Другая форма Y′CbCr указана в стандарте ITU-R BT.709 , в первую очередь для использования в HDTV . Более новая форма также используется в некоторых приложениях, ориентированных на компьютерные дисплеи, как sRGB (хотя матрица, используемая для формы sRGB YCbCr, sYCC , по-прежнему BT.601). В этом случае значения Kb и Kr различаются, но формулы для их использования одинаковы. Для ITU-R BT.709 константы следующие:

${\displaystyle {\begin{aligned}K_{B}&=0.0722\\K_{R}&=0.2126\\(K_{G}&=1-K_{B}-K_{R}=0.7152)\end{aligned}}}$

Эта форма Y′CbCr основана на модели RGB, которая более точно соответствует характеристикам излучения люминофора новых ЭЛТ и другого современного дисплейного оборудования. ^{[ необходима ссылка ]} Матрицы преобразования для BT.709 следующие:

${\displaystyle {\begin{aligned}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}&={\begin{bmatrix}0.2126&0.7152&0.0722\\-0.1146&-0.3854&0.5\\0.5&-0.4542&-0.0458\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}\\{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}&={\begin{bmatrix}1&0&1.5748\\1&-0.1873&-0.4681\\1&1.8556&0\end{bmatrix}}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}\end{aligned}}}$

Определения сигналов R', G' и B' также различаются между BT.709 и BT.601 и различаются в BT.601 в зависимости от типа используемой телевизионной системы (625-строчная, как в PAL и SECAM , или 525-строчная, как в NTSC ), а также различаются в других спецификациях. В разных конструкциях существуют различия в определениях координат цветности R, G и B, опорной белой точки, поддерживаемом диапазоне гаммы, точных функциях предварительной компенсации гаммы для получения R', G' и B' из R, G и B, а также в масштабировании и смещениях, которые должны применяться во время преобразования из R'G'B' в Y′CbCr. Таким образом, правильное преобразование Y′CbCr из одной формы в другую — это не просто вопрос инвертирования одной матрицы и применения другой. Фактически, когда Y′CbCr спроектирован идеально, значения K _B и K _R выводятся из точной спецификации основных цветовых сигналов RGB, так что сигнал яркости (Y′) максимально соответствует измерению яркости с поправкой на гамма-коррекцию (обычно основанному на измерениях CIE 1931 реакции зрительной системы человека на цветовые стимулы). ^[4]

Стандарт ITU-R BT.2020 использует ту же гамма-функцию, что и BT.709. Он определяет: ^[5]

• Непостоянная яркость Y'CbCr, похожа на предыдущие записи, за исключением других K _B и K _R .
• Постоянная яркость Y'cCbcCrc, формула, где Y' — это гамма-кодековая версия истинной яркости . ^[5]

Для обоих вариантов коэффициенты, полученные в результате праймериз, следующие:

${\displaystyle {\begin{aligned}K_{B}&=0.0593\\K_{R}&=0.2627\\(K_{G}&=1-K_{B}-K_{R}=0.6780)\end{aligned}}}$

Для NCL определение классическое: ; ; . Преобразование кодирования, как обычно, можно записать в виде матрицы. ^[5] Матрица декодирования для BT.2020-NCL имеет вид с 14 десятичными знаками:${\displaystyle Y'=0.2627R'+0.6780G'+0.0593B'}$${\displaystyle Cb=(B'-Y')/1.8814}$${\displaystyle Cr=(R'-Y')/1.4746}$

${\displaystyle {\begin{aligned}{\begin{bmatrix}R\\G\\B\end{bmatrix}}&={\begin{bmatrix}1&0&1.4746\\1&-0.16455312684366&-0.57135312684366\\1&1.8814&0\end{bmatrix}}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}\end{aligned}}}$

Меньшие значения в матрице не округляются; они являются точными значениями. Для систем с ограниченной точностью (например, 8 или 10 бит) может использоваться более низкая точность вышеуказанной матрицы, например, сохраняя только 6 цифр после десятичной точки. ^[6]

Версия CL, YcCbcCrc, кодирует: ^[5]

• ${\displaystyle Y'c=(0.2627R+0.6780G+0.0593B)'}$. Это гамма-функция, применяемая к истинной яркости, рассчитанной из линейного RGB.
• ${\displaystyle Cbc=(B'-Y'c)/(-2Nb)}$в противном случае . и являются теоретическими минимумом и максимумом, соответствующими гамме. Округленные «практические» значения равны , . Полный вывод можно найти в рекомендации. ^[5]${\displaystyle B'<Y'c}$${\displaystyle (B'-Y'c)/(2Pb)}$${\displaystyle Nb}$${\displaystyle Pb}$${\displaystyle (B'-Y'c)}$${\displaystyle Pb=0.7910}$${\displaystyle Nb=-0.9702}$
• ${\displaystyle Crc=(R'-Y'c)/(-2Nr)}$если иначе . Опять же, и являются теоретическими пределами. Округленные значения , .${\displaystyle R'<Y'c}$${\displaystyle (R'-Y'c)/(2Pr)}$${\displaystyle Pr}$${\displaystyle Nr}$${\displaystyle Pr=0.4969}$${\displaystyle Nr=-0.8591}$

Функция CL может использоваться, когда сохранение яркости имеет первостепенное значение (см.: Chroma subsampling § Gamma luminance error ), или когда «ожидается улучшение эффективности кодирования для доставки». Спецификация ссылается на отчет ITU-R BT.2246 по этому вопросу. ^[5] BT.2246 утверждает, что CL улучшил эффективность сжатия и сохранение яркости, но NCL будет более знакома персоналу, который ранее занимался смешиванием цветов и другими производственными практиками в HDTV YCbCr. ^[7]

BT.2020 не определяет PQ и, следовательно, HDR, он дополнительно определен в SMPTE ST 2084 и BT.2100 . BT.2100 представит использование IC _T C _P , полуперцепционного цветового пространства, полученного из линейного RGB с хорошей линейностью оттенков. Это «почти постоянная яркость». ^[8]

Стандарт SMPTE 240M (используемый в аналоговой системе телевидения высокой четкости MUSE ) определяет YCC с помощью следующих коэффициентов:

${\displaystyle {\begin{aligned}K_{B}&=0.087\\K_{R}&=0.212\end{aligned}}}$

Коэффициенты получены на основе основных цветов SMPTE 170M и точки белого, используемых в стандарте 240M.

Использование JFIF в JPEG поддерживает модифицированный Rec. 601 Y′CbCr, где Y′, C _B и C _R имеют полный 8-битный диапазон [0...255]. ^[9] Ниже приведены уравнения преобразования, выраженные с точностью до шести десятичных знаков. (Идеальные уравнения см. в ITU-T T.871. ^[10] ) Обратите внимание, что для следующих формул диапазон каждого входа (R,G,B) также является полным 8-битным диапазоном [0...255].

${\displaystyle {\begin{aligned}Y'&=&0&+(0.299&\cdot R'_{D})&+(0.587&\cdot G'_{D})&+(0.114&\cdot B'_{D})\\C_{B}&=&128&-(0.168736&\cdot R'_{D})&-(0.331264&\cdot G'_{D})&+(0.5&\cdot B'_{D})\\C_{R}&=&128&+(0.5&\cdot R'_{D})&-(0.418688&\cdot G'_{D})&-(0.081312&\cdot B'_{D})\end{aligned}}}$

И обратно:

${\displaystyle {\begin{aligned}R'_{D}&=&Y'&&&+1.402&\cdot (C_{R}-128)\\G'_{D}&=&Y'&-0.344136&\cdot (C_{B}-128)&-0.714136&\cdot (C_{R}-128)\\B'_{D}&=&Y'&+1.772&\cdot (C_{B}-128)&\end{aligned}}}$

Приведенное выше преобразование идентично sYCC , когда входные данные указаны как sRGB, за исключением того, что IEC 61966-2-1:1999/Amd1:2003 дает только четыре десятичных знака.

JPEG также определяет формат "YCCK" от Adobe для ввода CMYK . В этом формате значение "K" передается как есть, в то время как CMY используются для получения YCbCr с помощью указанной выше матрицы, предполагая , , и . В результате может использоваться аналогичный набор методов подвыборки. ^[11]${\displaystyle R=1-C}$${\displaystyle G=1-M}$${\displaystyle B=1-Y}$

${\displaystyle {\begin{aligned}K_{B}&=0.0713\\K_{R}&=0.2220\end{aligned}}}$

Эти коэффициенты не используются и никогда не использовались. ^[12]

H.273 также описывает системы постоянной и непостоянной яркости, которые выводятся строго из основных цветов и точки белого, так что такие ситуации, как основные цвета по умолчанию sRGB/BT.709 JPEG, использующие матрицу BT.601 (которая выводится из BT.470-6 System M), не возникают.

До разработки быстрых процессоров SIMD с плавающей точкой большинство цифровых реализаций RGB → Y′UV использовали целочисленную математику, в частности, аппроксимации с фиксированной точкой . Аппроксимация означает, что точность используемых чисел (входных данных, выходных данных и постоянных значений) ограничена, и, таким образом, потеря точности, обычно около последней двоичной цифры, принимается тем, кто использует эту опцию, как правило, в качестве компромисса для улучшения скорости вычислений.

Значения Y′ традиционно смещаются и масштабируются до диапазона [16, 235] (называемого студийным размахом или «уровнями ТВ»), а не используют полный диапазон [0, 255] (называемый полным размахом или «уровнями ПК»). Эта практика была стандартизирована в SMPTE-125M для того, чтобы компенсировать выбросы сигнала («звон») из-за фильтрации. ^[13] Значения U и V, которые могут быть положительными или отрицательными, суммируются с 128, чтобы сделать их всегда положительными, что дает студийный диапазон 16–240 для U и V. (Эти диапазоны важны при редактировании и производстве видео, поскольку использование неправильного диапазона приведет либо к изображению с «обрезанными» черными и белыми цветами, либо к изображению с низкой контрастностью.)

Эти матрицы округляют все факторы до ближайшей 1/256 единицы. В результате для каждого компонента формируется только одно 16-битное промежуточное значение, и простой сдвиг вправо с округлением (x + 128) >> 8может позаботиться о делении. ^[13]

Для студийного свинга:

${\displaystyle {\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}={\frac {1}{256}}{\begin{bmatrix}66&129&25\\-38&-74&112\\112&-94&-18\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}+{\begin{bmatrix}16\\128\\128\end{bmatrix}}}$

Для полного хода:

${\displaystyle {\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}={\frac {1}{256}}{\begin{bmatrix}77&150&29\\-43&-84&127\\127&-106&-21\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}+{\begin{bmatrix}0\\128\\128\end{bmatrix}}}$

Google Skia использовала указанную выше 8-битную полнодиапазонную матрицу, что приводило к небольшому эффекту позеленения на изображениях JPEG, закодированных устройствами Android, более заметному при повторном сохранении. Проблема была исправлена ​​в 2016 году, когда вместо нее использовалась более точная версия. Благодаря оптимизации SIMD в libjpeg-turbo точная версия на самом деле быстрее. ^[14]

Файлы RGB обычно кодируются в 8, 12, 16 или 24 бита на пиксель. В этих примерах мы предположим 24 бита на пиксель, что записывается как RGB888 . Стандартный формат байта — просто r0, g0, b0, r1, g1, b1, ....

Форматы упакованных пикселей YCbCr часто называют "YUV". Такие файлы могут быть закодированы в 12, 16 или 24 бита на пиксель. В зависимости от подвыборки форматы можно в основном описать как 4:4:4, 4:2:2 и 4:2:0p. Апостроф после Y часто опускается, как и "p" (для planar) после YUV420p. С точки зрения фактических форматов файлов, 4:2:0 является наиболее распространенным, так как данные более сокращены, а расширение файла обычно ".YUV". Соотношение между скоростью передачи данных и дискретизацией (A:B:C) определяется соотношением между Y к U и V каналом. ^{[15] [16]} Обозначение «YUV», за которым следуют три числа, неопределенно: три числа могут относиться к подвыборке (как это сделано в «YUV420») или к битовой глубине в каждом канале (как это сделано в «YUV565»). Однозначный способ обозначения этих форматов — через код FourCC . ^[17]

Для преобразования из RGB в YUV или обратно проще всего использовать RGB888 и 4:4:4. Для 4:1:1, 4:2:2 и 4:2:0 байты сначала необходимо преобразовать в 4:4:4.

4:4:4 прост, так как не выполняется группировка пикселей: разница заключается только в том, сколько бит дано каждому каналу и в их расположении. Базовая YUV3схема использует 3 байта на пиксель с порядком y0, u0, v0, y1, u1, v1(используя «u» для Cb и «v» для Cr; то же самое относится к содержимому ниже). ^[17] В компьютерах чаще можно увидеть AYUVформат, который добавляет альфа-канал и идет a0, y0, u0, v0, a1, y1, u1, v1, потому что с группами по 32 бита проще иметь дело. ^[15]

4:2:2 группирует 2 пикселя вместе по горизонтали в каждом концептуальном «контейнере». Два основных расположения: ^[16]

• YUY2: также называется YUYV, работает в формате y0, u, y1, v.

  

• UYVY: обратный YUY2 с перестановкой байтов, работает в формате u, y0, v, y1.

4:1:1 используется редко. Пиксели располагаются в горизонтальных группах по 4. ^[16]

4:2:0 используется очень часто. Основные форматы — IMC2, IMC4, YV12 и NV12. ^[16] Все эти четыре формата являются «плоскими», что означает, что значения Y, U и V сгруппированы вместе, а не перемешаны. Все они занимают 12 бит на пиксель, предполагая 8-битный канал.

• Сначала IMC2 размещает полные изображения в Y. Затем он располагает каждую строку цветности в порядке V ₀ ... V _n , U ₀ ... U _n , где n — количество выборок цветности в строке, равное половине ширины Y.
• IMC4 похож на IMC2, за исключением того, что он работает в U ₀ ... U _n , V ₀ ... V _n .
• I420 — более простая конструкция, и она используется чаще. Записывается все изображение в Y, затем изображение в U, затем все изображение в V.

  

• YV12 следует той же общей схеме, что и I420, только порядок между изображениями U и V поменян. ^[18]
• NV12, возможно, является наиболее часто используемым 8-битным форматом 4:2:0. Он используется по умолчанию для предварительного просмотра камеры Android . ^[19] Записывается все изображение в Y, за которым следуют чередующиеся строки, которые идут U ₀ , V ₀ , U ₁ , V ₁ и т. д.

Существуют также «плиточные» варианты плоских форматов. ^[20]

• Калькулятор Y′CbCr, включая BT.1886
• Чарльз Пойнтон — FAQ по цвету
• Чарльз Пойнтон — Видеоинженерия
• Визуализация цветового пространства
• Цветовые пространства YUV, YCbCr, YPbPr.
• Определение YCbCr

Программные ресурсы для упакованных пикселей:

• Кон, Майк. Y′UV422 в RGB с использованием SSE/Assembly
• libyuv
• pixfc-sse – библиотека C для преобразований цветовых форматов, оптимизированных для SSE
• Файлы YUV – Образцы/демонстрационные видеофайлы YUV/RGB во многих форматах YUV, помогут вам в тестировании.