XPIC

Эта статья может быть слишком технической для понимания большинства читателей . Пожалуйста, помогите улучшить ее, чтобы сделать ее понятной для неспециалистов , не удаляя технические детали. ( Ноябрь 2024 ) ( Узнайте, как и когда удалить это сообщение )

XPIC , или технология подавления кросс-поляризационных помех, представляет собой алгоритм подавления взаимных помех между двумя принимаемыми потоками в системе связи с поляризационным мультиплексированием .

Компенсатор кросс-поляризационных помех (известный как XPIC) — это метод обработки сигнала, реализованный на демодулированных полученных сигналах на уровне основной полосы частот. Обычно он необходим в системах мультиплексирования с поляризационным разделением : источники данных, которые должны быть переданы, кодируются и отображаются в модулирующие символы QAM на системной скорости символов и преобразуются с повышением частоты до несущей частоты, генерируя два радиопотока, излучаемых одной антенной с двойной поляризацией (см. диаграмму направленности параболической антенны ). Соответствующая антенна с двойной поляризацией расположена на удаленном объекте и подключена к двум приемникам, которые преобразуют радиопотоки с понижением частоты в сигналы основной полосы частот (BB H, BB V) .

Этот метод мультиплексирования/демультиплексирования основан на ожидаемом различении двух ортогональных поляризаций (XPD):

• идеальная, бесконечная XPD всей системы гарантирует, что каждый сигнал на приемниках содержит только сигнал, генерируемый соответствующим передатчиком (плюс любой тепловой шум);
• любой реальный, конечный уровень XPD вместо этого проявляется как частичная рекомбинация между двумя сигналами, так что приемники наблюдают помехи из-за утечки кросс-поляризации. Некоторые из факторов, вызывающих такие кросс-поляризационные помехи, перечислены в разделе Мультиплексирование с поляризационным разделением .

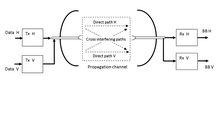
Как практическое следствие, на приемном участке два потока принимаются с остаточной взаимной помехой. Во многих практических случаях, особенно для модуляций M- QAM высокого уровня , система связи не может выдерживать испытываемые уровни кросс-поляризационной помехи, и необходимо улучшенное подавление. Две полученные поляризации на выходах антенны, обычно линейные горизонтальная H и вертикальная V, направляются каждая на приемник, выходной сигнал основной полосы которого далее обрабатывается специальной схемой отмены кросс-поляризации, обычно реализуемой как цифровой этап. Алгоритм XPIC достигает правильной реконструкции H путем суммирования V с H для отмены любых остаточных помех, и наоборот.

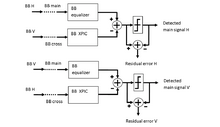
Процесс отмены обычно реализуется с использованием двух блоков: эквалайзера основной полосы и XPIC основной полосы. Выходной сигнал последнего вычитается из первого и затем отправляется на стадию принятия решения, отвечающую за получение оценки потока данных. Блоки выравнивания и XPIC обычно адаптивны для правильного отслеживания функции передачи канала, изменяющейся во времени: XPIC должен обеспечивать формирование полученного перекрестного сигнала, равного части перекрестных помех, влияющих на основной сигнал. Управление обратной связью для управления критериями адаптации происходит из измерения остаточной ошибки в блоке принятия решения.

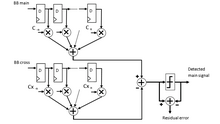
В примере оба блока основаны на типичной структуре цифрового фильтра с конечной импульсной характеристикой , коэффициенты которого не фиксированы, а адаптированы для минимизации подходящего функционала при воздействии на входной сигнал множественных задержек. ${\displaystyle J}$${\displaystyle D}$

Данный:

• ${\displaystyle \epsilon _{k}}$: остаточная комплексная ошибка в момент времени ,${\displaystyle к}$
• ${\displaystyle s_{k}^{(м)}}$: комплексная выборка основного принятого сигнала основной полосы пропускания в момент времени ,${\displaystyle к}$
• ${\displaystyle s_{k}^{(x)}}$: комплексная выборка сигнала, полученного в полосе пропускания, в момент времени ,${\displaystyle к}$
• ${\displaystyle C_{j,k}^{(m)}}$: комплексный коэффициент эквалайзера основной полосы частот на отводе j и момент времени ,${\displaystyle к}$
• ${\displaystyle C_{j,k}^{(x)}}$: комплексный коэффициент XPIC на кране j и момент времени ,${\displaystyle к}$
• ${\displaystyle j=-n,...,n}$: индекс крана
• ${\displaystyle y_{k}}$: результат отмены действия, подаваемого на устройство принятия решения в момент времени ,${\displaystyle к}$
• ${\displaystyle d_{k}}$: предполагаемые переданные данные в момент времени , поэтому = -${\displaystyle к}$${\displaystyle \epsilon _{k}}$${\displaystyle y_{k}}$${\displaystyle d_{k}}$
• ${\displaystyle \гамма}$: размер шага или коэффициент сжатия для адаптивности,

если минимизируемая функция представляет собой, например, среднюю мощность остаточной ошибки, алгоритм адаптирующего градиента предписывает, чтобы коэффициенты обновлялись после каждого временного шага следующим образом: ^[1]${\displaystyle J=E[|\epsilon _{k}|^{2}]}$${\displaystyle к}$

• ${\displaystyle C_{j,k+1}^{(m)}=C_{j,k}^{(m)}-\gamma \epsilon _{k}(s_{kj}^{(m)})^{*}}$;
• ${\displaystyle C_{j,k+1}^{(x)}=C_{j,k}^{(x)}-\гамма \epsilon _{k}(s_{kj}^{(x)})^{*}}$;

где звездочка обозначает комплексное сопряжение . Для этой базовой схемы не требуется никаких априорных знаний о передаваемых символах ( слепое или нулевое знание ).

Когда задержка равна периоду символа, блоки обозначаются как разнесенные по символам, в то время как если задержка составляет часть периода символа, то блоки называются разнесенными по дробным интервалам. ^[2] Другими минимизирующими функциями являются LMS с наименьшим средним квадратом или ZF с нулевым форсированием, в то время как архитектура может быть обратной связью по решению или дополнительно улучшена с помощью известных сигналов ( пилотный сигнал ).${\displaystyle D}$${\displaystyle D}$

• Патент на систему устранения помех с независимыми приемниками
• Патент на систему передачи кросс-поляризации с асинхронными приемниками
• Система связи
• Адаптивный эквалайзер