Граф Винера–Арайи
| Граф Винера-Арайи | |
|---|---|
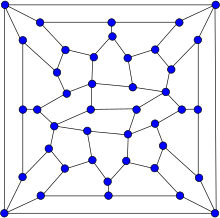 | |
| Вершины | 42 |
| Края | 67 |
| Радиус | 5 |
| Диаметр | 7 |
| Обхват | 4 |
| Автоморфизмы | 2 |
| Хроматическое число | 3 |
| Хроматический индекс | 4 |
| Характеристики | Гипогамильтонов планарный |
| Таблица графиков и параметров | |
Граф Винера–Арайи — это, в теории графов , граф на 42 вершинах с 67 ребрами. Он является гипогамильтоновым , что означает, что он сам по себе не имеет гамильтонова цикла , но каждый граф, образованный удалением из него одной вершины, является гамильтоновым . Он также является планарным .
История
Гипогамильтоновы графы были впервые изучены Сусселье в «Problèmes plaisants et délectables» (1963). [1] В 1967 году Линдгрен построил бесконечную последовательность гипогамильтоновых графов. [2] Сначала он сослался на Годена, Герца и Росси, [3] а затем на Бусакера и Саати [4] как на пионеров в этой области.
С самого начала известен наименьший гипогамильтонов граф : граф Петерсена . Однако охота за наименьшим плоским гипогамильтоновым графом продолжается. Этот вопрос впервые поднял Вацлав Хватал в 1973 году. [5] Первый возможный ответ был предоставлен в 1976 году Карстеном Томассеном , который продемонстрировал конструкцию из 105 вершин, 105-граф Томассена. [6] В 1979 году Хатцель улучшил этот результат с помощью плоского гипогамильтонова графа на 57 вершинах: графа Хатцеля. [7] Эта граница была снижена в 2007 году с помощью 48-графа Замфиреску. [8]
В 2009 году граф, построенный Габором Винером и Макото Арайей, стал (с его 42 вершинами) наименьшим известным плоским гипогамильтоновым графом . [9] [10] В своей статье Винер и Арайя предположили, что их граф является оптимальным, утверждая, что его порядок ( 42 ), по-видимому, является ответом на Главный вопрос жизни, Вселенной и всего такого из романа Дугласа Адамса «Автостопом по Галактике» . Однако впоследствии были обнаружены меньшие плоские гипогамильтоновы графы. [11]
Ссылки
- ^ Сусселье, Р. (1963), Проблема №. 29: Le cercle des irascibles , vol. 7, преподобный Франс. Речи. Opérationnelle, стр. 405–406.
- ^ Линдгрен, У. Ф. (1967), «Бесконечный класс гипогамильтоновых графов», American Mathematical Monthly , 74 (9): 1087–1089, doi : 10.2307/2313617, JSTOR 2313617, MR 0224501
- ^ Годен, Т.; Герц, П.; Росси (1964), «Решение проблемы № 29», преподобный Франс. Речи. Opérationnelle (на французском языке), 8 : 214–218.
- ^ Бусакер, РГ; Саати, ТЛ (1965), Конечные графы и сети
- ^ Chvátal, V. (1973), «Флип-флопы в гипогамильтоновых графах», Canadian Mathematical Bulletin , 16 : 33–41, doi : 10.4153/cmb-1973-008-9 , MR 0371722
- ^ Томассен, Карстен (1976), «Планарные и бесконечные гипогамильтоновы и гипотрассируемые графы», Дискретная математика , 14 (4): 377–389, doi :10.1016/0012-365x(76)90071-6, MR 0422086
- ^ Хацель, Вольфганг (1979), "Ein planarer гипогамильтоншерный граф с 57 узлами", Mathematische Annalen (на немецком языке), 243 (3): 213–216, doi : 10.1007/BF01424541, MR 0548801, S2CID 121794449
- ^ Замфиреску, Кэрол Т.; Замфиреску, Тудор И. (2007), «Планарный гипогамильтонов граф с 48 вершинами», Журнал теории графов , 55 (4): 338–342, doi :10.1002/jgt.20241, MR 2336805, S2CID 260477281
- ↑ Винер, Габор; Арайя, Макото (20 апреля 2009 г.), Главный вопрос , arXiv : 0904.3012 , Bibcode : 2009arXiv0904.3012W.
- ^ Винер, Габор; Арайя, Макото (2011), «О плоских гипогамильтоновых графах», Журнал теории графов , 67 (1): 55–68, doi :10.1002/jgt.20513, MR 2809563, S2CID 5340663.
- ^ Джуянде, Мохаммадреза; Маккей, Брендан Д .; Остергорд, Патрик Р.Дж.; Петтерссон, Вилле Х.; Замфиреску, Кэрол Т. (2017), «Плоские гипогамильтоновы графы на 40 вершинах», Journal of Graph Theory , 84 (2): 121–133, arXiv : 1302.2698 , doi : 10.1002/jgt.22015, MR 3601121, S2CID 5535167
Внешние ссылки
- Вайсштейн, Эрик В. , «График Винера-Арайи», MathWorld