Общеизвестное текстовое представление геометрии
Известный текст ( WKT ) — это язык разметки текста для представления объектов векторной геометрии . Двоичный эквивалент, известный как известный двоичный код ( WKB ), используется для передачи и хранения той же информации в более компактной форме, удобной для компьютерной обработки, но не читаемой человеком. Форматы были первоначально определены Open Geospatial Consortium (OGC) и описаны в их Simple Feature Access . [1] Текущее стандартное определение содержится в стандарте ISO/IEC 13249-3:2016. [2]
Геометрические объекты
WKT может представлять следующие отдельные геометрические объекты:
- Точка , Многоточечная
- LineString , MultiLineString
- Многоугольник , Мультиполигон, Треугольник
- МногогранныйПоверхность
- TIN ( Триангулированная нерегулярная сеть )
- GeometryCollection
Координаты для геометрий могут быть 2D ( x , y ), 3D ( x , y , z ), 4D ( x , y , z , m ) со значением m , которое является частью линейной системы отсчета или 2D со значением m ( x , y , m ). Трехмерные геометрии обозначаются буквой "Z" после типа геометрии, а геометрии с линейной системой отсчета обозначаются буквой "M" после типа геометрии. Пустые геометрии, не содержащие координат, можно указать с помощью символа EMPTYпосле имени типа.
Геометрии WKT используются во всех спецификациях OGC и присутствуют в приложениях, которые реализуют эти спецификации. Например, PostGIS содержит функции, которые могут преобразовывать геометрии в представление WKT и обратно, делая их читаемыми человеком.
Стандартное определение OGC требует, чтобы многоугольник был топологически замкнутым. В нем также говорится, что если внешнее линейное кольцо многоугольника определено в направлении против часовой стрелки, то оно будет видно «сверху». Любые внутренние линейные кольца должны быть определены противоположным образом по сравнению с внешним кольцом, в данном случае по часовой стрелке. [3]
| Тип | Примеры | |
|---|---|---|
| Точка |  | POINT (30 10) |
| ЛинияСтрока |  | LINESTRING (30 10, 10 30, 40 40) |
| Полигон |  | POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10)) |
 | POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10), | |
| Тип | Примеры | |
|---|---|---|
| Мультипоинт | 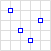 | MULTIPOINT ((10 40), (40 30), (20 20), (30 10)) |
MULTIPOINT (10 40, 40 30, 20 20, 30 10) | ||
| МногострочныйСтрока |  | MULTILINESTRING ((10 10, 20 20, 10 40), |
| Мультиполигон |  | MULTIPOLYGON (((30 20, 45 40, 10 40, 30 20)), |
 | MULTIPOLYGON (((40 40, 20 45, 45 30, 40 40)), | |
| GeometryCollection |  | GEOMETRYCOLLECTION (POINT (40 10), |
Ниже приведены некоторые другие примеры геометрических строк WKT: (Примечание: каждый элемент ниже представляет собой отдельную геометрию.)
GEOMETRYCOLLECTION(POINT(4 6),LINESTRING(4 6,7 10))ТОЧКА ЗМ (1 1 5 60)ТОЧКА М (1 1 80)ТОЧКА ПУСТОМУЛЬТИПОЛИГОН ПУСТОЙТРЕУГОЛЬНИК((0 0 0,0 1 0,1 1 0,0 0 0))ИНН(((0 0 0, 0 0 1, 0 1 0, 0 0 0)), ((0 0 0, 0 1 0, 1 1 0, 0 0 0)))МНОГОГРАННАЯ ПОВЕРХНОСТЬ Z (ЗАПЛАНКИ ((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)), ((0 0 0, 0 1 0, 0 1 1, 0 0 1, 0 0 0)), ((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)), ((1 1 1, 1 0 1, 0 0 1, 0 1 1, 1 1 1)), ((1 1 1, 1 0 1, 1 0 0, 1 1 0, 1 1 1)), ((1 1 1, 1 1 0, 0 1 0, 0 1 1, 1 1 1)) )Известный двоичный файл
Известные двоичные (WKB) представления обычно отображаются в шестнадцатеричных строках.
Первый байт указывает порядок байтов данных:
0x00: обратный порядок байтов0x01: прямой порядок байтов
Следующие 4 байта представляют собой 32-битное беззнаковое целое число для типа геометрии, как описано ниже:
| Тип | 2D | З | М | ЗМ |
|---|---|---|---|---|
| Геометрия | 0 | 1000 | 2000 | 3000 |
| Точка | 1 | 1001 | 2001 | 3001 |
| ЛинияСтрока | 2 | 1002 | 2002 | 3002 |
| Полигон | 3 | 1003 | 2003 | 3003 |
| Мультипоинт | 4 | 1004 | 2004 | 3004 |
| МногострочныйСтрока | 5 | 1005 | 2005 | 3005 |
| Мультиполигон | 6 | 1006 | 2006 | 3006 |
| GeometryCollection | 7 | 1007 | 2007 | 3007 |
| КруговаяСтрока | 8 | 1008 | 2008 | 3008 |
| CompoundCurve | 9 | 1009 | 2009 | 3009 |
| КривойМногоугольник | 10 | 1010 | 2010 | 3010 |
| МультиКурв | 11 | 1011 | 2011 | 3011 |
| MultiSurface | 12 | 1012 | 2012 | 3012 |
| Изгиб | 13 | 1013 | 2013 | 3013 |
| Поверхность | 14 | 1014 | 2014 | 3014 |
| МногогранныйПоверхность | 15 | 1015 | 2015 | 3015 |
| ИНН | 16 | 1016 | 2016 | 3016 |
| Треугольник | 17 | 1017 | 2017 | 3017 |
| Круг | 18 | 1018 | 2018 | 3018 |
| ГеодезическаяСтруна | 19 | 1019 | 2019 | 3019 |
| ЭллиптическаяКривая | 20 | 1020 | 2020 | 3020 |
| NurbsCurve | 21 | 1021 | 2021 | 3021 |
| клотоидный | 22 | 1022 | 2022 | 3022 |
| СпиральКривая | 23 | 1023 | 2023 | 3023 |
| CompoundSurface | 24 | 1024 | 2024 | 3024 |
| BrepSolid | | 1025 | | |
| АффинноеРасположение | 102 | 1102 | | |
Каждый тип данных имеет уникальную структуру данных, например, количество точек или линейных колец, за которыми следуют координаты в 64-битных двойных числах.
Например, геометрия POINT(2.0 4.0)представлена как: , где:000000000140000000000000004010000000000000
- 1-байтовое целое
00или 0: big endian - 4-байтовое целое число
00000001или 1: ТОЧКА (2D) - 8-байтовое число с плавающей точкой
4000000000000000или 2.0: x -координата - 8-байтовое число с плавающей точкой
4010000000000000или 4.0: координата y
Варианты формата
- EWKT и EWKB – расширенный общеизвестный текст/двоичный код
- Специфичный для PostGIS формат , включающий идентификатор пространственной системы отсчета (SRID) и до 4 значений ординат (XYZM). [4] [5] Например:
SRID=4326;POINT(-44.3 60.1)для определения координат долготы/широты с использованием системы отсчета WGS 84. Он также поддерживает круговые кривые, следующие элементы, названные (но не полностью определенные) в исходном WKT: CircularString, CompoundCurve, CurvePolygon и CompoundSurface. [6] - Текст AGF – Формат геометрии Autodesk
- Расширение стандарта OGC (на тот момент) для включения изогнутых элементов; наиболее заметно использовалось в MapGuide . [7]
Смотрите также
Ссылки
- ^ Херринг, Джон Р., ред. (2011-05-28), Стандарт внедрения OpenGIS® для географической информации – Простой доступ к объектам – Часть 1: Общая архитектура, Открытый геопространственный консорциум , получено 2019-01-28
- ^ Информационные технологии — Языки баз данных — Мультимедиа и пакеты приложений SQL — Часть 3: Пространственные (5-е изд.), ISO , 2016-01-15 , получено 2019-01-28
- ^ См. спецификацию реализации OGC для географической информации – простой доступ к объектам, раздел 6.1.11.1. http://www.opengeospatial.org/standards/sfa
- ^ "Postgis/Postgis". GitHub . 6 октября 2021 г.
- ^ "ST_GeomFromEWKT" . Получено 2022-11-25 .
- ^ "Глава 4: Использование PostGIS: Управление данными и запросы". postgis.net . Получено 2021-07-30 .
- ^ "Справочник API MapGuide: Текст AGF" . Получено 14.09.2023 .
Внешние ссылки
- Простая спецификация доступа к функциям
- Пространственный стандарт ISO (за это взимается плата)
- Нотация BNF для WKT. Архивировано 03.01.2023 на Wayback Machine.
- Обозначение EBNF для WKT
- Онлайн-преобразование между представлениями геометрических объектов