Кривая удержания воды

This article may be confusing or unclear to readers. Please help clarify the article. There might be a discussion about this on the talk page. (September 2017) (Learn how and when to remove this message)

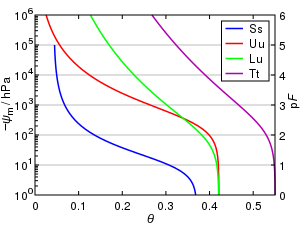
Кривая удержания воды - это соотношение между содержанием воды , θ , и потенциалом почвенной влаги , ψ. Кривая почвенной влажности характерна для различных типов почв и также называется характеристикой почвенной влажности .

Он используется для прогнозирования запаса почвенной воды, водоснабжения растений ( полевая вместимость ) и стабильности почвенных агрегатов . Из-за гистерезисного эффекта заполнения и осушения пор водой можно выделить различные кривые смачивания и высыхания.

Общие черты кривой удержания воды можно увидеть на рисунке, на котором объемное содержание воды, θ , нанесено на график в зависимости от матричного потенциала, . При потенциалах, близких к нулю, почва близка к насыщению, и вода удерживается в почве в основном капиллярными силами. По мере уменьшения θ связывание воды становится сильнее, и при малых потенциалах (более отрицательных, приближающихся к точке увядания ) вода прочно связана в самых маленьких порах, в точках контакта между зернами и в виде пленок, связанных адсорбционными силами вокруг частиц.${\displaystyle \Psi _{m}}$

Песчаные почвы будут включать в себя в основном капиллярное связывание и, следовательно, будут высвобождать большую часть воды при более высоких потенциалах, в то время как глинистые почвы с адгезионным и осмотическим связыванием будут высвобождать воду при более низких (более отрицательных) потенциалах. При любом заданном потенциале торфяные почвы обычно будут демонстрировать гораздо более высокое содержание влаги, чем глинистые почвы, которые, как ожидается, будут удерживать больше воды, чем песчаные почвы. Водоудерживающая способность любой почвы обусловлена ​​пористостью и характером связей в почве.

Форму кривых удержания воды можно охарактеризовать несколькими моделями, одна из которых известна как модель Ван Генухтена: ^[1]

${\displaystyle \theta (\psi )=\theta _{r}+{\frac {\theta _{s}-\theta _{r}}{\left[1+(\alpha |\psi |)^{n}\right]^{1-1/n}}}}$

где

${\displaystyle \theta (\psi )}$кривая удержания воды [L ³ L ⁻³ ];

${\displaystyle |\psi |}$- давление всасывания ([л] или см вод. ст.);

${\displaystyle \theta _{s}}$содержание насыщенной воды [л ³ л ⁻³ ];

${\displaystyle \theta _{r}}$остаточное содержание воды [л ³ л ⁻³ ];

${\displaystyle \alpha }$связана с обратной величиной всасывания воздуха на входе ([L ⁻¹ ] или см ⁻¹ ); и,${\displaystyle \alpha >0}$

${\displaystyle n}$является мерой распределения размеров пор (безразмерной).${\displaystyle n>1}$

На основе этой параметризации была разработана модель прогнозирования формы зависимости ненасыщенной гидравлической проводимости от насыщенности и давления. ^[2]

В 1907 году Эдгар Бэкингем создал первую кривую удержания воды. ^[2] Она была измерена и построена для шести почв, различающихся по текстуре от песка до глины. Данные были получены в результате экспериментов, проведенных на почвенных колоннах высотой 48 дюймов, где постоянный уровень воды поддерживался примерно на 2 дюйма выше дна за счет периодического добавления воды из боковой трубки. Верхние концы были закрыты для предотвращения испарения.

Параметры Ван Генухтена ( и ) могут быть определены с помощью полевых или лабораторных испытаний. Одним из методов является метод мгновенного профиля, ^[3] , где содержание воды (или эффективная насыщенность ) определяется для серии измерений давления всасывания . Из-за нелинейности уравнения для решения параметров Ван Генухтена можно использовать численные методы, такие как нелинейный метод наименьших квадратов . ^{[4] [5]} Точность оцененных параметров будет зависеть от качества полученного набора данных ( и ). Когда кривые удержания воды подгоняются с помощью нелинейного метода наименьших квадратов, может возникнуть структурная переоценка или недооценка. В этих случаях представление кривых удержания воды может быть улучшено с точки зрения точности и неопределенности путем применения регрессии гауссовского процесса к остаткам, которые получены после нелинейного метода наименьших квадратов. Это в основном из-за корреляции между точками данных, которая учитывается с помощью регрессии гауссовского процесса через функцию ядра. ^[6]${\displaystyle \alpha }$${\displaystyle n}$ ${\displaystyle \theta }$ ${\displaystyle Se}$${\displaystyle \psi }$${\displaystyle \theta }$${\displaystyle \psi }$

• Почвенная вода (удержание)

• Брэди, NC (1999). Природа и свойства почв (12-е изд.). Верхняя Сэддл-Ривер, Нью-Джерси: Prentice-Hall. стр. 183–9. ISBN 0-13-852444-0.

• База данных модели UNSODA для ненасыщенных гидравлических свойств грунта (UNSODA viewer)
• SWRC Fit подгоняет гидравлические модели почвы под данные по водоудержанию почвы