Матрица преобразования
В линейной алгебре линейные преобразования могут быть представлены матрицами . Если — линейное преобразование, отображающее в , а — вектор-столбец с записями, то для некоторой матрицы , называемой матрицей преобразования . [ необходима ссылка ] Обратите внимание, что имеет строки и столбцы, тогда как преобразование происходит из в . Существуют альтернативные выражения матриц преобразования, включающие векторы -строки , которые предпочитают некоторые авторы. [1] [2]
Использует
Матрицы позволяют отображать произвольные линейные преобразования в единообразном формате, пригодном для вычислений. [3] Это также позволяет легко составлять преобразования (путем умножения их матриц).
Линейные преобразования — не единственные, которые могут быть представлены матрицами. Некоторые преобразования, которые являются нелинейными в n-мерном евклидовом пространстве R n , могут быть представлены как линейные преобразования в n +1-мерном пространстве R n +1 . К ним относятся как аффинные преобразования (такие как перенос ), так и проективные преобразования . По этой причине матрицы преобразования 4×4 широко используются в трехмерной компьютерной графике . Эти n +1-мерные матрицы преобразования называются, в зависимости от их применения, матрицами аффинного преобразования , матрицами проективного преобразования или, в более общем смысле, матрицами нелинейного преобразования . Относительно n -мерной матрицы, n +1-мерная матрица может быть описана как расширенная матрица .
В физических науках активное преобразование — это преобразование, которое фактически изменяет физическое положение системы и имеет смысл даже при отсутствии системы координат , тогда как пассивное преобразование — это изменение координатного описания физической системы ( изменение базиса ). Различие между активными и пассивными преобразованиями важно. По умолчанию под преобразованием математики обычно подразумевают активные преобразования, в то время как физики могут подразумевать и то, и другое.
Иными словами, пассивное преобразование относится к описанию одного и того же объекта, рассматриваемого с двух разных систем координат.
Нахождение матрицы преобразования
Если имеется линейное преобразование в функциональной форме, то легко определить матрицу преобразования A , преобразуя каждый из векторов стандартного базиса с помощью T , а затем вставляя результат в столбцы матрицы. Другими словами,
Например, функция является линейным преобразованием. Применение вышеописанного процесса (предположим, что n = 2 в этом случае) показывает, что
Матричное представление векторов и операторов зависит от выбранного базиса; аналогичная матрица получится из альтернативного базиса. Тем не менее, метод нахождения компонентов остается тем же.
Для уточнения вектор можно представить в виде базисных векторов с координатами :
Теперь выразим результат преобразования матрицы A по , в заданном базисе:
Элементы матрицы A определяются для заданного базиса E путем применения A к каждому и наблюдения за вектором отклика
Это уравнение определяет искомые элементы j - го столбца матрицы A. [4 ]
Собственный базис и диагональная матрица
Тем не менее, существует специальный базис для оператора, в котором компоненты образуют диагональную матрицу и, таким образом, сложность умножения уменьшается до n . Диагональ означает, что все коэффициенты, за исключением , равны нулю, оставляя только один член в сумме выше. Выжившие диагональные элементы, , известны как собственные значения и обозначены в определяющем уравнении, которое уменьшается до . Результирующее уравнение известно как уравнение собственных значений . [5] Собственные векторы и собственные значения выводятся из него с помощью характеристического полинома .
С помощью диагонализации часто можно осуществлять перевод в собственные базисы и из них.
Примеры в 2 измерениях
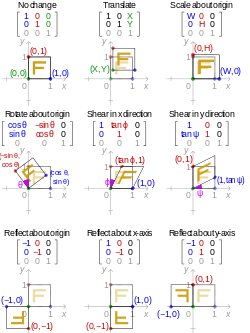
Наиболее распространенные геометрические преобразования , которые сохраняют начало координат фиксированным, являются линейными, включая вращение, масштабирование, сдвиг, отражение и ортогональную проекцию; если аффинное преобразование не является чистым переносом, оно сохраняет некоторую точку фиксированной, и эта точка может быть выбрана в качестве начала координат, чтобы сделать преобразование линейным. В двух измерениях линейные преобразования могут быть представлены с помощью матрицы преобразования 2×2.
Растяжка
Растяжение в плоскости xy — это линейное преобразование, которое увеличивает все расстояния в определенном направлении на постоянный множитель, но не влияет на расстояния в перпендикулярном направлении. Мы рассматриваем только растяжения вдоль осей x и y. Растяжение вдоль оси x имеет вид x' = kx ; y' = y для некоторой положительной константы k . (Обратите внимание, что если k > 1 , то это действительно «растяжение»; если k < 1 , то это технически «сжатие», но мы все равно называем это растяжением. Кроме того, если k = 1 , то преобразование является тождественным, т. е. оно не имеет никакого эффекта.)
Матрица, связанная с растяжением в k раз вдоль оси x, определяется выражением:
Аналогично, растяжение в k раз вдоль оси y имеет вид x' = x ; y' = ky , поэтому матрица, связанная с этим преобразованием, имеет вид
Сжимание
Если два растяжения выше объединить с обратными значениями, то матрица преобразования представляет собой отображение сжатия : квадрат со сторонами, параллельными осям, преобразуется в прямоугольник, имеющий ту же площадь, что и квадрат. Обратное растяжение и сжатие оставляют площадь инвариантной.
Вращение
Для поворота на угол θ против часовой стрелки (положительное направление) вокруг начала координат функциональная форма имеет вид и . Записанная в матричной форме, это становится: [6]
Аналогично, для вращения по часовой стрелке (отрицательное направление) вокруг начала координат функциональная форма имеет вид , а матричная форма — вид:
Эти формулы предполагают, что ось x направлена вправо, а ось y — вверх.
Стрижка
Для картирования сдвига (визуально похожего на наклон) есть две возможности.
Сдвиг, параллельный оси x , имеет и . Записанное в матричной форме, это становится:
Сдвиг, параллельный оси y , имеет и , который имеет матричную форму:
Отражение
Для отражения относительно прямой, проходящей через начало координат, пусть будет вектором в направлении прямой. Затем используйте матрицу преобразования:
Ортогональная проекция
Чтобы спроецировать вектор ортогонально на линию, проходящую через начало координат, пусть будет вектором в направлении линии. Затем используйте матрицу преобразования:
Как и в случае отражений, ортогональная проекция на прямую, не проходящую через начало координат, является аффинным, а не линейным преобразованием.
Параллельные проекции также являются линейными преобразованиями и могут быть представлены просто матрицей. Однако перспективные проекции таковыми не являются, и для их представления матрицей можно использовать однородные координаты .
Примеры в 3D компьютерной графике
Вращение
Матрица для поворота на угол θ вокруг любой оси, заданной единичным вектором ( x , y , z ), равна [7]
Отражение
Чтобы отразить точку через плоскость (проходящую через начало координат), можно использовать , где — единичная матрица 3×3, а — трехмерный единичный вектор для векторной нормали плоскости. Если норма L 2 для , , и равна единице, матрицу преобразования можно выразить как:
Обратите внимание, что это частные случаи отражения Хаусхолдера в двух и трех измерениях. Отражение относительно прямой или плоскости, которая не проходит через начало координат, не является линейным преобразованием — это аффинное преобразование — как матрица аффинного преобразования 4×4, ее можно выразить следующим образом (предполагая, что нормаль — единичный вектор): где для некоторой точки на плоскости, или, что эквивалентно, .
Если 4-й компонент вектора равен 0 вместо 1, то отражается только направление вектора, а его величина остается неизменной, как если бы он был отражен относительно параллельной плоскости, проходящей через начало координат. Это полезное свойство, поскольку оно позволяет преобразовывать как позиционные векторы, так и нормальные векторы с одной и той же матрицей. Для дальнейшего объяснения см. однородные координаты и аффинные преобразования ниже.
Составление и инвертирование преобразований
Одной из основных причин использования матриц для представления линейных преобразований является то, что преобразования затем можно легко компоновать и инвертировать.
Композиция выполняется путем умножения матриц . Векторы строк и столбцов обрабатываются матрицами, строки слева и столбцы справа. Поскольку текст читается слева направо, при составлении матриц преобразования предпочтительны векторы столбцов:
Если A и B являются матрицами двух линейных преобразований, то эффект первого применения A , а затем B к вектору-столбцу определяется по формуле:
Другими словами, матрица комбинированного преобразования A, за которой следует B, является просто произведением отдельных матриц.
Когда A является обратимой матрицей, существует матрица A −1 , которая представляет собой преобразование, которое «отменяет» A , поскольку ее композиция с A является единичной матрицей . В некоторых практических приложениях инверсию можно вычислить с помощью общих алгоритмов инверсии или путем выполнения обратных операций (которые имеют очевидную геометрическую интерпретацию, например, вращение в противоположном направлении) и последующего их составления в обратном порядке. Матрицы отражения являются особым случаем, поскольку они являются своими собственными обратными и не требуют отдельного вычисления.
Другие виды преобразований
Аффинные преобразования
Для представления аффинных преобразований с помощью матриц мы можем использовать однородные координаты . Это означает представление 2-вектора ( x , y ) как 3-вектора ( x , y , 1), и аналогично для более высоких измерений. Используя эту систему, перенос может быть выражен с помощью умножения матриц. Функциональная форма становится:
Все обычные линейные преобразования включены в набор аффинных преобразований и могут быть описаны как упрощенная форма аффинных преобразований. Таким образом, любое линейное преобразование также может быть представлено общей матрицей преобразования. Последняя получается путем расширения соответствующей матрицы линейного преобразования на одну строку и столбец, заполняя дополнительное пространство нулями, за исключением нижнего правого угла, который должен быть установлен в 1. Например, матрица вращения против часовой стрелки сверху становится:
Используя матрицы преобразования, содержащие однородные координаты, переносы становятся линейными и, таким образом, могут быть легко смешаны со всеми другими типами преобразований. Причина в том, что действительная плоскость отображается в плоскость w = 1 в реальном проективном пространстве, и поэтому перенос в реальном евклидовом пространстве может быть представлен как сдвиг в реальном проективном пространстве. Хотя перенос является нелинейным преобразованием в 2-мерном или 3-мерном евклидовом пространстве, описываемом декартовыми координатами (т. е. его нельзя объединить с другими преобразованиями, сохраняя коммутативность и другие свойства), в 3-мерном или 4-мерном проективном пространстве, описываемом однородными координатами, он становится простым линейным преобразованием (сдвигом ) .
Больше аффинных преобразований можно получить путем композиции двух или более аффинных преобразований. Например, если заданы перенос T' с вектором, поворот R на угол θ против часовой стрелки , масштабирование S с множителями и перенос T вектора , то результат M T'RST будет: [8]
При использовании аффинных преобразований однородный компонент координатного вектора (обычно называемый w ) никогда не изменится. Поэтому можно смело предположить, что он всегда равен 1, и игнорировать его. Однако это неверно при использовании перспективных проекций.
Перспективная проекция

Другим типом преобразования, важным в 3D компьютерной графике , является перспективная проекция . В то время как параллельные проекции используются для проецирования точек на плоскость изображения вдоль параллельных линий, перспективная проекция проецирует точки на плоскость изображения вдоль линий, исходящих из одной точки, называемой центром проекции. Это означает, что объект имеет меньшую проекцию, когда он находится далеко от центра проекции, и большую проекцию, когда он ближе (см. также обратную функцию ).
Простейшая перспективная проекция использует начало координат как центр проекции, а плоскость в качестве плоскости изображения. Функциональная форма этого преобразования тогда ; . Мы можем выразить это в однородных координатах как:
После выполнения умножения матриц однородный компонент будет равен значению , а остальные три не изменятся. Поэтому для обратного отображения в действительную плоскость мы должны выполнить однородное деление или перспективное деление, разделив каждый компонент на :
Более сложные перспективные проекции можно составить, объединив эту проекцию с вращениями, масштабированием, переносами и сдвигами, чтобы переместить плоскость изображения и центр проекции в желаемое место.
Смотрите также
- 3D проекция
- Изменение основы
- Исправление изображения
- Поза (компьютерное зрение)
- Жесткая трансформация
- Трансформация (функция)
- Трансформационная геометрия
Ссылки
- ^ Рафаэль Арци (1965) Линейная геометрия
- ^ JWP Hirschfeld (1979) Проективная геометрия конечных полей , Clarendon Press
- ^ Джентл, Джеймс Э. (2007). «Матричные преобразования и факторизации». Матричная алгебра: теория, вычисления и приложения в статистике . Springer. ISBN 9780387708737.
- ^ Ниринг, Джеймс (2010). "Глава 7.3 Примеры операторов" (PDF) . Математические инструменты для физики. ISBN 978-0486482125. Получено 1 января 2012 г. .
- ^ Ниринг, Джеймс (2010). "Глава 7.9: Собственные значения и собственные векторы" (PDF) . Математические инструменты для физики. ISBN 978-0486482125. Получено 1 января 2012 г. .
- ^ "Lecture Notes" (PDF) . ocw.mit.edu . Получено 2024-07-28 .
- ^ Szymanski, John E. (1989). Основы математики для инженеров-электронщиков: Модели и приложения . Taylor & Francis. стр. 154. ISBN 0278000681.
- ^ Седрик Жюль (25 февраля 2015 г.). «Выпечка матриц двумерного преобразования».
Внешние ссылки
- Страница Матрицы Практические примеры в POV-Ray
- Справочная страница - Вращение осей
- Калькулятор линейного преобразования
- Апплет преобразования — создание матриц из двумерных преобразований и наоборот.
- Преобразование координат при вращении в 2D
- Excel Fun — создание 3D-графики из электронной таблицы















![{\displaystyle [\mathbf {v} ]_{E}={\begin{bmatrix}v_{1}&v_{2}&\cdots &v_{n}\end{bmatrix}}^{\mathrm {T} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c191b7fbcd3d20b54295dbd8203c79c0bac76f)
![{\displaystyle \mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+\cdots +v_{n}\mathbf {e} _ {n}=\sum _{i}v_{i}\mathbf {e} _{i}=E[\mathbf {v} ]_{Е}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd7e2feda21844936fee6fcb19e447df7c275853)
![{\displaystyle {\begin{aligned}A(\mathbf {v})&=A\left(\sum _{i}v_{i}\mathbf {e} _{i}\right)=\sum _{ i}{v_{i}A(\mathbf {e} _{i})}\\&={\begin{bmatrix}A(\mathbf {e} _{1})&A(\mathbf {e} _{2})&\cdots &A(\mathbf {e} _{n})\end{bmatrix}}[\mathbf {v} ]_{E}= A\cdot [\mathbf {v} ]_{E}\\[3pt]&={\begin{bmatrix}\mathbf {e} _{1}&\mathbf {e} _{2}&\cdots &\mathbf {e} _{n}\end{bmatrix}}{\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1 }&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n, n}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78e7c729b432477f302eb9fd9d627f2bfa5b56ab)





















































