Верхний плоский рисунок
Граф с непересекающимися и направленными вверх ребрами
Восходящий плоский рисунок
Этот плоский DAG не имеет направленного вверх рисунка, поскольку его источник и сток не могут одновременно находиться на одной и той же грани.

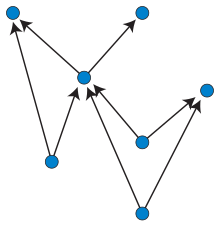
В рисовании графа восходящее планарное рисование направленного ациклического графа является вложением графа в евклидову плоскость , в которой ребра представлены как непересекающиеся монотонные восходящие кривые. То есть кривая, представляющая каждое ребро, должна обладать свойством, что каждая горизонтальная линия пересекает ее не более чем в одной точке, и никакие два ребра не могут пересекаться, кроме как в общей конечной точке. [1] В этом смысле это идеальный случай для послойного рисования графа , стиля рисования графа, в котором ребра являются монотонными кривыми, которые могут пересекаться, но в которых пересечения должны быть минимизированы.

Характеристика

Направленный ациклический граф должен быть планарным , чтобы иметь восходящий планарный рисунок, но не каждый планарный ациклический граф имеет такой рисунок. Среди плоских направленных ациклических графов с одним источником (вершиной без входящих ребер) и стоком (вершиной без исходящих ребер) графы с восходящими планарными рисунками являются st -планарные графы , планарные графы, в которых источник и сток принадлежат одной и той же грани по крайней мере одного из планарных вложений графа. В более общем смысле, граф G имеет восходящий планарный рисунок тогда и только тогда, когда он направлен и ацикличен, и является подграфом st -планарного графа на том же множестве вершин. [2]

В восходящем вложении наборы входящих и исходящих ребер, инцидентных каждой вершине, являются смежными в циклическом порядке ребер в вершине. Плоское вложение данного направленного ациклического графа называется бимодальным, если оно обладает этим свойством. Кроме того, угол между двумя последовательными ребрами с одинаковой ориентацией в данной вершине может быть помечен как малый , если он меньше π, или большой , если он больше π. Каждый источник или сток должен иметь ровно один большой угол, а каждая вершина, которая не является ни источником, ни стоком, не должна иметь ни одного. Кроме того, каждая внутренняя грань рисунка должна иметь на два малых угла больше, чем больших, а внешняя грань должна иметь на два больших угла больше, чем малых. Согласованное назначение — это маркировка углов, которая удовлетворяет этим свойствам; каждое восходящее вложение имеет согласованное назначение. Наоборот, каждый направленный ациклический граф, имеющий бимодальное планарное вложение с последовательным назначением, имеет восходящий планарный рисунок, который может быть построен из него за линейное время. [3]

Другая характеристика возможна для графов с одним источником. В этом случае восходящее планарное вложение должно иметь источник на внешней грани, и каждый неориентированный цикл графа должен иметь по крайней мере одну вершину, в которую входят оба ребра цикла (например, вершину с самым высоким расположением на рисунке). Наоборот, если вложение обладает обоими этими свойствами, то оно эквивалентно восходящему вложению. [4]

Сложность вычислений

Известно, что несколько особых случаев проверки восходящей планарности возможны за полиномиальное время :

  • Проверка того, является ли граф st -планарным, может быть выполнена за линейное время путем добавления ребра из s в t и проверки того, является ли оставшийся граф планарным. По тем же принципам можно построить восходящий планарный рисунок (если он существует) направленного ациклического графа с одним источником и стоком за линейное время. [5]
  • Тестирование того, может ли ориентированный граф с фиксированным планарным вложением быть нарисован вверх планарно, с вложением, согласованным с заданным, может быть выполнено путем проверки того, что вложение является бимодальным и моделирования задачи согласованного назначения как задачи сетевого потока . Время выполнения линейно по размеру входного графа и полиномиально по количеству его источников и стоков. [6]
  • Поскольку ориентированные многогранные графы имеют уникальное планарное вложение, существование восходящего планарного рисунка для этих графов может быть проверено за полиномиальное время. [7]
  • Проверка того, имеет ли внешнепланарный ориентированный ациклический граф восходящий планарный рисунок, также является полиномиальной. [8]
  • Каждый последовательно-параллельный граф , ориентированный в соответствии с последовательно-параллельной структурой, является восходящим планарным. Восходящий планарный рисунок может быть построен непосредственно из последовательно-параллельного разложения графа. [9] В более общем случае произвольные ориентации неориентированных последовательно-параллельных графов могут быть проверены на восходящую планарность за полиномиальное время. [10]
  • Каждое ориентированное дерево является направленным вверх планарным. [9]
  • Каждый двудольный планарный граф, ребра которого ориентированы последовательно от одной стороны двудольного графа к другой, является восходящим планарным графом [9] [11]
  • Известен более сложный алгоритм полиномиального времени для проверки восходящей планарности графов, имеющих один источник, но несколько стоков, или наоборот. [12]
  • Тестирование восходящей планарности может быть выполнено за полиномиальное время, когда имеется постоянное число трехсвязных компонентов и вершин разреза, и является разрешимым с фиксированными параметрами в этих двух числах. [13] Он также разрешим с фиксированными параметрами в цикломатическом числе входного графа. [14] Он также разрешим с фиксированными параметрами в числе источников (т. е. вершин без входящих ребер) [15]
  • Если y -координаты всех вершин фиксированы, то выбор x -координат, который делает рисунок вверх плоским, может быть найден за полиномиальное время. [16]

Однако задача определения того, имеет ли плоский ориентированный ациклический граф с несколькими источниками и стоками восходящий плоский рисунок, является NP-полной . [17]

Требования к чертежу прямых линий и площади

Теорема Фари утверждает, что каждый планарный граф имеет рисунок, в котором его ребра представлены отрезками прямых линий, и то же самое верно для восходящего планарного рисунка: каждый восходящий планарный граф имеет прямой восходящий планарный рисунок. [18] Прямолинейный восходящий рисунок транзитивно редуцированного st -планарного графа может быть получен с помощью техники доминантного рисунка , при этом все вершины имеют целочисленные координаты в пределах сетки n  ×  n . [19] Однако некоторые другие восходящие планарные графы могут потребовать экспоненциальной площади во всех их прямолинейных восходящих планарных рисунках. [18] Если выбор вложения фиксирован, даже ориентированные последовательные параллельные графы и ориентированные деревья могут потребовать экспоненциальной площади. [20]

Диаграммы Хассе

Восходящие планарные рисунки особенно важны для диаграмм Хассе частично упорядоченных множеств , поскольку эти диаграммы обычно требуется рисовать снизу вверх. В терминах теории графов они соответствуют транзитивно редуцированным направленным ациклическим графам; такой граф может быть образован из отношения покрытия частичного порядка, а сам частичный порядок образует отношение достижимости в графе. Если частично упорядоченное множество имеет один минимальный элемент, имеет один максимальный элемент и имеет восходящий планарный рисунок, то оно обязательно должно образовывать решетку , множество, в котором каждая пара элементов имеет уникальную наибольшую нижнюю границу и уникальную наименьшую верхнюю границу. [21] Диаграмма Хассе решетки является планарной тогда и только тогда, когда ее размерность порядка не превышает двух. [22] Однако некоторые частичные порядки размерности два и с одним минимальным и максимальным элементом не имеют восходящего планарного рисунка (возьмем порядок, определенный транзитивным замыканием ). а < б , а < с , б < г , б < е , с < г , с < е , г < ф , е < ф {\displaystyle а<б,а<в,б<г,б<е,в<г,в<е,г<е,е<е}

Ссылки

Сноски
  1. ^ Гарг и Тамассия (1995); Ди Баттиста и др. (1998).
  2. ^ Гарг и Тамассия (1995), стр. 111–112; Ди Баттиста и др. (1998), 6.1 «Включение в планарный st -граф», стр. 172–179; Ди Баттиста и Тамассия (1988); Келли (1987).
  3. ^ Гарг и Тамассия (1995), стр. 112–115; Ди Баттиста и др. (1998), 6.2 «Углы в рисунках вверх», стр. 180–188; Бертолацци и Ди Баттиста (1991); Бертолацци и др. (1994).
  4. ^ Гарг и Тамассия (1995), стр. 115; Ди Баттиста и др. (1998), 6.7.2 «Запрещенные циклы для орграфов с одним источником», стр. 209–210; Томассен (1989).
  5. ^ Гарг и Тамассия (1995), стр. 119; Ди Баттиста и др. (1998), с. 179.
  6. ^ Гарг и Тамассия (1995), стр. 119–121; Ди Баттиста и др. (1998), 6.3 «Тестирование восходящей планарности встроенных орграфов», стр. 188–192; Бертолацци и Ди Баттиста (1991); Бертолацци и др. (1994); Аббаси, Хили и Рекстин (2010).
  7. ^ Ди Баттиста и др. (1998), стр. 191–192; Бертолацци и Ди Баттиста (1991); Бертолацци и др. (1994).
  8. ^ Гарг и Тамассия (1995), стр. 125–126; Ди Баттиста и др. (1998), 6.7.1 «Внепланарный орграф», с. 209; Папакостас (1995).
  9. ^ abc Di Battista et al. (1998), 6.7.4 «Некоторые классы восходящих планарных орграфов», стр. 212.
  10. ^ Дидимо, Джордано и Лиотта (2009).
  11. ^ Ди Баттиста, Лю и соперник (1990).
  12. ^ Garg & Tamassia (1995), стр. 122–125; Di Battista et al. (1998), 6.5 «Оптимальное тестирование восходящей планарности одноисточниковых диграфов», стр. 195–200; Hutton & Lubiw (1996); Bertolazzi et al. (1998).
  13. ^ Чан (2004); Хили и Линч (2006).
  14. ^ Хили и Линч (2006).
  15. ^ Чаплик и др. (2022)
  16. ^ Юнгер и Лейперт (1999).
  17. ^ Гарг и Тамассиа (1995), стр. 126–132; Ди Баттиста и др. (1998), 6.6 «Тестирование восходящей планарности является NP-полным», стр. 201–209; Гарг и Тамассиа (2001).
  18. ^ аб Ди Баттиста и Фрати (2012); Ди Баттиста, Тамассия и Толлис (1992).
  19. ^ Ди Баттиста и др. (1998), 4.7 «Рисунки доминирования», стр. 112–127; Ди Баттиста, Тамассия и Толлис (1992).
  20. ^ Ди Баттиста и Фрати (2012); Бертолацци и др. (1994); Фрати (2008).
  21. ^ Ди Баттиста и др. (1998), 6.7.3 «Запрещенные конструкции для решеток», стр. 210–212; Платт (1976).
  22. ^ Гарг и Тамассиа (1995), стр. 118; Бейкер, Фишберн и Робертс (1972).
Опросы и учебники
  • Ди Баттиста, Джузеппе; Идс, Питер ; Тамассиа, Роберто ; Толлис, Иоаннис Г. (1998), «Поток и восходящая планарность», Рисование графов: алгоритмы визуализации графов , Prentice Hall , стр. 171–213, ISBN 978-0-13-301615-4.
  • Ди Баттиста, Джузеппе; Фрати, Фабрицио (2012), «Рисование деревьев, внешнепланарных графов, последовательно-параллельных графов и планарных графов в малой области», Тридцать эссе по геометрической теории графов , Алгоритмы и комбинаторика, т. 29, Springer, стр. 121–165, doi :10.1007/978-1-4614-0110-0_9, ISBN 9781461401100. Раздел 5, «Восходящие рисунки», стр. 149–151.
  • Гарг, Ашим; Тамассиа, Роберто (1995), «Тестирование восходящей планарности», Order , 12 (2): 109–133, doi :10.1007/BF01108622, MR  1354797, S2CID  14183717.
Научные статьи
  • Аббаси, Сармад; Хили, Патрик; Рекстин, Эймал (2010), «Улучшение времени выполнения встроенного тестирования восходящей планарности», Information Processing Letters , 110 (7): 274–278, doi :10.1016/j.ipl.2010.02.004, MR  2642837.
  • Бейкер, КА; Фишберн, ПК; Робертс, ФС (1972), «Частичные порядки размерности 2», Сети , 2 (1): 11–28, doi :10.1002/net.3230020103.
  • Бертолацци, Паола; Коэн, Роберт Ф.; Ди Баттиста, Джузеппе; Тамассиа, Роберто ; Толлис, Иоаннис Г. (1994), «Как нарисовать последовательно-параллельный орграф», Международный журнал вычислительной геометрии и приложений , 4 (4): 385–402, doi :10.1142/S0218195994000215, MR  1310911.
  • Бертолацци, Паола; Ди Баттиста, Джузеппе (1991), «О тестировании трехсвязных орграфов методом восходящего рисования», Труды седьмого ежегодного симпозиума по вычислительной геометрии (SCG '91, Норт-Конвей, Нью-Гемпшир, США), Нью-Йорк, штат Нью-Йорк, США: ACM, стр. 272–280, doi :10.1145/109648.109679, ISBN 0-89791-426-0, S2CID  18306721.
  • Бертолацци, П.; Ди Баттиста, Г.; Лиотта, Г.; Маннино, К. (1994), «Восходящие рисунки трехсвязных орграфов», Algorithmica , 12 (6): 476–497, doi : 10.1007/BF01188716, MR  1297810, S2CID  33167313.
  • Бертолацци, Паола; Ди Баттиста, Джузеппе; Маннино, Карло; Тамассиа, Роберто (1998), «Оптимальное тестирование восходящей планарности орграфов с одним источником», SIAM Journal on Computing , 27 (1): 132–169, doi : 10.1137/S0097539794279626, MR  1614821.
  • Чан, Хуберт (2004), «Параметризованный алгоритм для тестирования восходящей планарности», Труды 12-го Европейского симпозиума по алгоритмам (ESA '04) , Lecture Notes in Computer Science, т. 3221, Springer-Verlag, стр. 157–168, doi :10.1007/978-3-540-30140-0_16, ISBN 978-3-540-23025-0.
  • Ди Баттиста, Джузеппе; Лю, Вэй-Пин; Ривал, Иван (1990), «Двудольные графы, восходящие рисунки и планарность», Information Processing Letters , 36 (6): 317–322, doi :10.1016/0020-0190(90)90045-Y, MR  1084490.
  • Ди Баттиста, Джузеппе; Тамассиа, Роберто (1988), «Алгоритмы для плоских представлений ациклических орграфов», Теоретическая информатика , 61 (2–3): 175–198, doi : 10.1016/0304-3975(88)90123-5 , MR  0980241.
  • Di Battista, Giuseppe; Tamassia, Roberto ; Tollis, Ioannis G. (1992), «Требование площади и отображение симметрии плоских восходящих рисунков», Discrete and Computational Geometry , 7 (4): 381–401, doi : 10.1007/BF02187850 , MR  1148953.
  • Дидимо, Вальтер; Джордано, Франческо; Лиотта, Джузеппе (2009), «Тестирование восходящей спиральности и восходящей планарности», SIAM Journal on Discrete Mathematics , 23 (4): 1842–1899, doi :10.1137/070696854, MR  2594962, S2CID  26154284.
  • Фрати, Фабрицио (2008), «О минимальных площадных планарных восходящих рисунках ориентированных деревьев и других семейств ориентированных ациклических графов», Международный журнал вычислительной геометрии и приложений , 18 (3): 251–271, doi :10.1142/S021819590800260X, MR  2424444.
  • Гарг, Ашим; Тамассиа, Роберто (2001), «О вычислительной сложности тестирования восходящей и прямолинейной планарности», SIAM Journal on Computing , 31 (2): 601–625, doi :10.1137/S0097539794277123, MR  1861292, S2CID  15691098.
  • Хили, Патрик; Линч, Кароль (2006), «Два фиксированных параметра для проверки восходящей планарности», Международный журнал основ компьютерной науки , 17 (5): 1095–1114, doi :10.1142/S0129054106004285.
  • Хаттон, Майкл Д.; Любив, Анна (1996), «Восходящее планарное рисование ациклических орграфов с одним источником», SIAM Journal on Computing , 25 (2): 291–311, doi :10.1137/S0097539792235906, MR  1379303. Впервые представлен на 2-м симпозиуме ACM-SIAM по дискретным алгоритмам, 1991 г.
  • Юнгер, Михаэль; Лейперт, Себастьян (1999), «Уровень планарного вложения за линейное время», Graph Drawing (Proc. GD '99) , Lecture Notes in Computer Science, т. 1731, стр. 72–81, doi : 10.1007/3-540-46648-7_7 , ISBN 978-3-540-66904-3.
  • Келли, Дэвид (1987), «Основы плоских упорядоченных множеств», Дискретная математика , 63 (2–3): 197–216, doi : 10.1016/0012-365X(87)90008-2 , MR  0885497.
  • Papakostas, Achilleas (1995), "Upward planarity testing of externalplanar dags (extended abstract)", Graph Drawing: DIMACS International Workshop, GD '94, Princeton, New Jersey, USA, October 10–12, 1994, Proceedings , Lecture Notes in Computer Science, vol. 894, Berlin: Springer, pp. 298–306, doi : 10.1007/3-540-58950-3_385 , ISBN 978-3-540-58950-1, МР  1337518.
  • Платт, CR (1976), «Планарные решетки и планарные графы», Журнал комбинаторной теории , Сер. B, 21 (1): 30–39, doi : 10.1016/0095-8956(76)90024-1.
  • Томассен, Карстен (1989), «Планарные ациклические ориентированные графы», Order , 5 (4): 349–361, doi :10.1007/BF00353654, MR  1010384, S2CID  121445872.
  • Чаплик, Стивен; Ди Джакомо, Эмилио; Фрати, Фабрицио; Ганиан, Роберт; Рафтопулу, Хрисанти Н.; Симонов, Кирилл (2022), «Параметризованные алгоритмы для восходящей планарности», 38-й Международный симпозиум по вычислительной геометрии, SoCG , Международные труды Лейбница по информатике (LIPIcs), т. 224, стр. 26:1–26:16, doi : 10.4230/LIPIcs.SoCG.2022.26 , ISBN 9783959772273
Получено с "https://en.wikipedia.org/w/index.php?title=Upward_planar_drawing&oldid=1237435432"