Эксперимент Траутона–Нобла
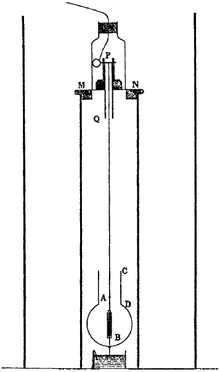
Эксперимент Траутона –Нобла был попыткой обнаружить движение Земли через светоносный эфир и был проведен в 1901–1903 годах Фредериком Томасом Траутоном и HR Ноблом. Он был основан на предположении Джорджа Фицджеральда о том, что заряженный параллельный плоский конденсатор, движущийся через эфир, должен ориентироваться перпендикулярно движению. Как и более ранний эксперимент Майкельсона–Морли , Траутон и Нобл получили нулевой результат : никакого движения относительно эфира обнаружить не удалось. [1] [2] Этот нулевой результат был воспроизведен с возрастающей чувствительностью Рудольфом Томашеком (1925, 1926), Чейзом (1926, 1927) и Хейденом в 1994 году. [3] [4] [5] [6] [7] [8] Такие экспериментальные результаты, как теперь считается, согласуются со специальной теорией относительности , отражают справедливость принципа относительности и отсутствие какой-либо абсолютной системы покоя (или эфира). Эксперимент является проверкой специальной теории относительности .
Эксперимент Траутона–Нобла также связан с мысленными экспериментами , такими как «парадокс Траутона–Нобла» и «прямоугольный рычаг» или «парадокс Льюиса–Толмена». Было предложено несколько решений для разрешения этого вида парадокса, все из которых согласуются со специальной теорией относительности.
Эксперимент Траутона–Нобла
В эксперименте подвешенный параллельный плоский конденсатор удерживается тонким торсионным волокном и заряжается. Если бы теория эфира была верна, изменение уравнений Максвелла из-за движения Земли через эфир привело бы к крутящему моменту, заставляющему пластины выравниваться перпендикулярно движению. Это определяется по формуле:
где - крутящий момент, энергия конденсатора, угол между нормалью пластины и скоростью.
С другой стороны, утверждение специальной теории относительности о том, что уравнения Максвелла инвариантны для всех систем отсчета, движущихся с постоянной скоростью, предсказывало бы отсутствие крутящего момента (нулевой результат). Таким образом, если только эфир не был каким-то образом зафиксирован относительно Земли, эксперимент является проверкой того, какое из этих двух описаний является более точным. Его нулевой результат, таким образом, подтверждает лоренц-инвариантность специальной теории относительности.
Однако, в то время как отрицательный экспериментальный результат может быть легко объяснен в системе покоя устройства, объяснение с точки зрения несопутствующей системы (касающееся вопроса, должен ли возникать тот же крутящий момент, что и в «эфирной системе», описанной выше, или крутящий момент не возникает вообще) гораздо сложнее и называется «парадоксом Траутона–Нобла», который можно решить несколькими способами (см. Решения ниже).
Парадокс рычага под прямым углом
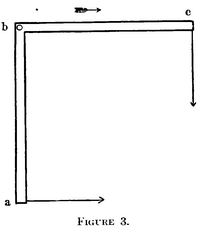
Парадокс Траутона–Нобла по сути эквивалентен мысленному эксперименту , называемому парадоксом рычага под прямым углом , впервые обсуждаемому Гилбертом Ньютоном Льюисом и Ричардом Чейзом Толменом в 1909 году. [9] Предположим, что есть рычаг под прямым углом с концами abc . В его системе покоя силы, направленные к ba и к bc, должны быть равны для достижения равновесия, поэтому закон рычага не даёт никакого крутящего момента:
где крутящий момент, а остаточная длина одного плеча рычага. Однако из-за сокращения длины ba длиннее bc в несопутствующей системе, поэтому закон рычага дает:
Видно, что крутящий момент не равен нулю, что, по-видимому, заставило бы рычаг вращаться в несопутствующей системе отсчета. Поскольку вращения не наблюдается, Льюис и Толман пришли к выводу, что крутящего момента не существует, поэтому:
Однако, как показал Макс фон Лауэ (1911), [10] это противоречит релятивистским выражениям силы,
что дает
При применении закона рычага возникает следующий крутящий момент:
Что по сути является той же проблемой, что и в парадоксе Траутона–Нобла.
Решения
Подробный релятивистский анализ как парадокса Траутона–Нобла, так и парадокса рычага с прямым углом требует осторожности, чтобы правильно согласовать, например, эффекты, наблюдаемые наблюдателями в разных системах отсчета, но в конечном итоге все такие теоретические описания показывают, что дают один и тот же результат. В обоих случаях кажущийся чистый крутящий момент на объекте (при наблюдении из определенной системы отсчета) не приводит к какому-либо вращению объекта, и в обоих случаях это объясняется правильным учетом, релятивистским способом, преобразования всех соответствующих сил, импульсов и ускорений, производимых ими. Ранняя история описаний этого эксперимента рассмотрена Янссеном (1995). [11]
ток Лауэ
Первое решение парадокса Траутона–Нобла было дано Хендриком Лоренцом (1904). Его результат основан на предположении, что крутящий момент и импульс, обусловленные электростатическими силами, компенсируются крутящим моментом и импульсом, обусловленными молекулярными силами. [12] Однако не существует известного механизма того, как преобразование Лоренца могло бы создавать такие молекулярные силы. Кроме того, если два точечных заряда соединены гибкой струной, никакая молекулярная сила не могла бы создавать вращающий момент.
Это было далее разработано Максом фон Лауэ (1911), который дал стандартное решение для такого рода парадоксов. Оно было основано на так называемой « инерции энергии » в ее общей формулировке Макса Планка . Согласно Лауэ, поток энергии, связанный с определенным импульсом («ток Лауэ»), создается в движущихся телах упругими напряжениями. Результирующий механический момент в случае эксперимента Траутона–Нобла составляет:
и в прямоугольном рычаге:
что точно компенсирует электромагнитный момент, упомянутый выше, таким образом, вращение не происходит в обоих случаях. Или, другими словами: электромагнитный момент фактически необходим для равномерного движения тела, т.е. для того, чтобы препятствовать вращению тела из-за механического момента, вызванного упругими напряжениями. [10] [13] [14] [15]
С тех пор появилось много статей, в которых подробно рассматривался ток Лауэ, предлагались некоторые модификации или новые интерпретации, а также рассматривались различные варианты «скрытого» импульса. [16]
Сила и ускорение
Решение без компенсирующих сил или переопределений силы и равновесия было опубликовано Ричардом К. Толменом [17] и Полом Софусом Эпштейном [18] [19] в 1911 году. Они применили понятие релятивистской массы, которая была разной в продольном направлении и поперечном направлении, так что сила и ускорение не всегда имеют одинаковое направление. Роль, которую играет концепция силы в теории относительности, сильно отличается от роли в ньютоновской механике. Аналогичный вывод был сделан Франклином (2006) [20] , используя инвариантную массу, которая не менялась с направлением, но используя тот факт, что направление релятивистского ускорения отличается от направления релятивистской силы.
Эпштейн представил себе безмассовый стержень с концами OM , который закреплен в точке O , а частица с массой покоя m закреплена в точке M (см. [1]). Стержень образует угол с осью y'. Теперь сила, направленная к O , приложена в точке M , и равновесие в ее системе покоя достигается при . Как уже было показано выше, эти силы имеют вид в несопутствующей системе отсчета:
Таким образом .
Итак, результирующая сила не указывает напрямую из O в M. Приводит ли это к вращению стержня? Нет, потому что Эпштейн теперь рассматривал ускорения, вызванные двумя силами. Он использовал концепцию релятивистской массы, которая была разной в продольном направлении и поперечном направлении, так что
- .
Релятивистские выражения в случае, когда масса m ускоряется этими двумя силами в продольном и поперечном направлении, имеют вид
- .
Таким образом .
Франклин использовал релятивистскую связь между силой и ускорением,
Используя это соотношение между релятивистской силой и ускорением, можно показать, что в этой системе не происходит никакого вращения. Аналогичные соображения следует применить к прямоугольному рычагу и парадоксу Траутона–Нобла. Таким образом, парадоксы разрешены, поскольку два ускорения (как векторы) указывают на центр тяжести системы, хотя две силы — нет.
Смотрите также
Ссылки
- ^ ab FT Trouton и HR Noble, «Механические силы, действующие на заряженный электрический конденсатор, движущийся в пространстве», Phil. Trans. Royal Soc. A 202 , 165–181 (1903).
- ^ FT Trouton и HR Noble, «Силы, действующие на заряженный конденсатор, движущийся в пространстве». Proc. Royal Soc. 74 (479): 132-133 (1903).
- ^ Р. Томашек (1925). «Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen I». Аннален дер Физик . 78 (24): 743–756. Бибкод : 1926АнП...383..743Т. дои : 10.1002/andp.19263832403.
- ^ Р. Томашек (1926). «Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen II». Аннален дер Физик . 80 (13): 509–514. Бибкод : 1926АнП...385..509Т. дои : 10.1002/andp.19263851304.
- ^ Карл Т. Чейз (1926). «Повторение эксперимента Траутона-Нобла по эфирному ветру» (PDF) . Physical Review . 28 (2): 378–383. Bibcode : 1926PhRv...28..378C. doi : 10.1103/PhysRev.28.378.
- ^ Карл Т. Чейз (1927). «Эксперимент по эфирному ветру Траутона–Нобла». Physical Review . 30 (4): 516–519. Bibcode : 1927PhRv...30..516C. doi : 10.1103/PhysRev.30.516.
- ^ Р. Томашек (1927). «Bemerkung zu meinen Versuchen zur Auffindung elektrodynamischer Wirkungen in großen Höhen». Аннален дер Физик . 84 (17): 161–162. Бибкод : 1927АнП...389..161Т. дои : 10.1002/andp.19273891709.
- ^ HC Hayden (1994). "Высокочувствительный эксперимент Троутона–Нобла". Review of Scientific Instruments . 65 (4): 788–792. Bibcode : 1994RScI...65..788H. doi : 10.1063/1.1144955.
- ^ Льюис, Гилберт Н.; Толман, Ричард К. (1909), , Труды Американской академии искусств и наук , 44 (25): 709–726, doi :10.2307/20022495, JSTOR 20022495
- ^ аб Лауэ, Макс фон (1911). «Ein Beispiel zur Dynamik der Relativitätstheorie». Verhandlungen der Deutschen Physikalischen Gesellschaft . 13 : 513–518.
- Перевод на английский язык с Викиресурса: Пример динамики теории относительности
- ^ Янссен (1995), см. «Дополнительная литература»
- ^ Лоренц, Хендрик Антон (1904), , Труды Королевской Нидерландской академии искусств и наук , 6 : 809–831, Bibcode : 1903KNAB....6..809L
- ^ Лауэ, Макс фон (1911). «Динамика теории относительности». Аннален дер Физик . 340 (8): 524–542. Бибкод : 1911АнП...340..524Л. дои : 10.1002/andp.19113400808.
- Перевод на английский язык с Wikisource: О динамике теории относительности
- ^ Лауэ, Макс фон (1911). «Bemerkungen zum Hebelgesetz в теории относительности». Physikalische Zeitschrift . 12 : 1008–1010.
- Перевод на английский язык с Викиресурса: Замечания о законе рычага в теории относительности
- ^ Лауэ, Макс фон (1912). «Zur Theorie des Versures von Trouton und Noble». Аннален дер Физик . 343 (7): 370–384. Бибкод : 1912АнП...343..370Л. дои : 10.1002/andp.19123430705.
- Перевод на английский язык из Wikisource: О теории эксперимента Траутона и Нобла
- ↑ См. «дополнительное чтение», особенно Никерсон/МакЭдори (1975), Сингал (1993), Тьюкольский (1996), Ефименко (1999), Джексон (2004).
- ^ Толмен, Ричард К. (1911), «Неньютоновская механика: направление силы и ускорения», Philosophical Magazine , 22 (129): 458–463, doi :10.1080/14786440908637142
- ^ Эпштейн, PS (1911). «Убер релятивистская статистика». Аннален дер Физик . 341 (14): 779–795. Бибкод : 1911АнП...341..779Е. дои : 10.1002/andp.19113411404.
- Перевод на английский язык с Wikisource: Concerning Relativistic Statics
- ^ Эпштейн, PS (1927). «Конференция по эксперименту Майкельсона-Морли». Вклад обсерватории Маунт-Вильсон . 373 : 45–49. Bibcode :1928CMWCI.373...43E.
- ^ Франклин, Джерролд (2006). «Отсутствие вращения в эксперименте Троутона Нобла». European Journal of Physics . 27 (5): 1251–1256. arXiv : physics/0603110 . Bibcode :2006EJPh...27.1251F. doi :10.1088/0143-0807/27/5/024. S2CID 16934275.
Дальнейшее чтение
- История
- Мишель Янссен, «Сравнение теории эфира Лоренца и специальной теории относительности в свете экспериментов Траутона и Нобла», докторская диссертация (1995). Онлайн: TOC, pref., intro-I, 1, 2, intro-II, 3, 4, ссылки.
- Янссен, Мишель ХП (2008), «Проведение границы между кинематикой и динамикой в специальной теории относительности», Симпозиум по времени и относительности , 40 (1): 1–76, Bibcode : 2009SHPMP..40...26J, doi : 10.1016/j.shpsb.2008.06.004
- Учебники
- Толмен, Р. К. (1917), «Рычаг под прямым углом», Теория относительности движения , Беркли: Издательство Калифорнийского университета, стр. 539–776, 152–153
- Паули, Вольфганг (1981) [1921]. «Применения к особым случаям. Эксперимент Траутона и Нобла». Теория относительности . Нью-Йорк: Довер. С. 127–130. ISBN 978-0-486-64152-2.
- Панофски, Вольфганг; Филлипс, Мельба (2005) [1962]. Классическое электричество и магнетизм . Дувр. стр. 274, 349. ISBN 978-0-486-43924-2.
- Джексон, Джон Д. (1998). Классическая электродинамика (3-е изд.). Wiley. ISBN 978-0-471-30932-1.
- Франклин, Дж. (2017). Классический электромагнетизм (2-е изд.). Довер. С. 467–468. ISBN 978-0-486-81371-4.
- Гамба, А. (1967). «Физические величины в различных системах отсчета в соответствии с теорией относительности». Американский журнал физики . 35 (2): 83–89. Bibcode : 1967AmJPh..35...83G. doi : 10.1119/1.1973974.
- Батлер, Дж. У. (1968). «Об эксперименте Траутона-Нобла». Американский журнал физики . 36 (11): 936–941. Bibcode : 1968AmJPh..36..936B. CiteSeerX 10.1.1.144.9274 . doi : 10.1119/1.1974358.
- Аранофф, С. (1969). «Моменты и угловой момент в системе, находящейся в равновесии в специальной теории относительности». American Journal of Physics . 37 (4): 453–454. Bibcode : 1969AmJPh..37..453A. doi : 10.1119/1.1975612.
- Furry, WH (1969). «Примеры распределений импульса в электромагнитном поле и в веществе». American Journal of Physics . 37 (6): 621–636. Bibcode : 1969AmJPh..37..621F. doi : 10.1119/1.1975729.
- Батлер, Дж. В. (1969). «Предлагаемый 4-вектор электромагнитного импульса-энергии для заряженных тел». Американский журнал физики . 37 (12): 1258–1272. Bibcode : 1969AmJPh..37.1258B. doi : 10.1119/1.1975297.
- Батлер, Дж. В. (1970). «Парадокс рычага Льюиса-Толмена». Американский журнал физики . 38 (3): 360–368. Bibcode : 1970AmJPh..38..360B. doi : 10.1119/1.1976326.
- Рорлих, Ф. (1970). «Электромагнитный импульс, энергия и масса». Американский журнал физики . 38 (11): 1310–1316. Bibcode : 1970AmJPh..38.1310R. doi : 10.1119/1.1976082.
- Сирс, Фрэнсис В. (1972). «Еще один релятивистский парадокс». Американский журнал физики . 40 (5): 771–773. Bibcode : 1972AmJPh..40..771S. doi : 10.1119/1.1986643.
- Аранофф, С. (1973). «Еще о прямоугольном рычаге в равновесии в специальной теории относительности». American Journal of Physics . 41 (9): 1108–1109. Bibcode : 1973AmJPh..41.1108A. doi : 10.1119/1.1987485.
- Никерсон, Дж. Чарльз; Макэдори, Роберт Т. (1975). «Парадокс Траутона-Нобла». Американский журнал физики . 43 (7): 615–621. Bibcode : 1975AmJPh..43..615N. doi : 10.1119/1.9761 .
- Каваллери, Г.; Грён, О.; Спавьери, Г.; Спинелли, Г. (1978). «Комментарий к статье «Парадокс рычага под прямым углом» Дж. К. Никерсона и Р. Т. Макэдори». Американский журнал физики . 46 (1): 108–109. Bibcode : 1978AmJPh..46..108C. doi : 10.1119/1.11106.
- Грён, О. (1978). «Релятивистская статика и Ф. У. Сирс». American Journal of Physics . 46 (3): 249–250. Bibcode : 1978AmJPh..46..249G. doi : 10.1119/1.11164 .
- Холстейн, Барри Р.; Свифт, Артур Р. (1982). «Гибкая струна в специальной теории относительности». American Journal of Physics . 50 (10): 887–889. Bibcode : 1982AmJPh..50..887H. doi : 10.1119/1.13002.
- Сингал, Ашок К. (1993). «Об «объяснении» нулевых результатов эксперимента Траутона-Нобла». American Journal of Physics . 61 (5): 428–433. Bibcode : 1993AmJPh..61..428S. doi : 10.1119/1.17236.
- Teukolsky, Saul A. (1996). "Повторное объяснение эксперимента Траутона-Нобла" (PDF) . American Journal of Physics . 64 (9): 1104–1109. Bibcode :1996AmJPh..64.1104T. doi :10.1119/1.18329.
- Джексон, Дж. Д. (2004). «Крутящий момент или его отсутствие? Простое движение заряженной частицы, наблюдаемое в различных инерциальных системах отсчета». American Journal of Physics . 72 (12): 1484–1487. Bibcode :2004AmJPh..72.1484J. doi :10.1119/1.1783902.
- Агиррегабирия, Дж. М.; Эрнандес, А.; Ривас, М. (1982). «Парадокс, подобный Льюису-Толмену». European Journal of Physics . 3 (1): 30–33. Bibcode : 1982EJPh....3...30A. doi : 10.1088/0143-0807/3/1/008. S2CID 250832120.
- Франклин, Джерролд (2006). «Отсутствие вращения в эксперименте Троутона Нобла». European Journal of Physics . 27 (5): 1251–1256. arXiv : physics/0603110 . Bibcode :2006EJPh...27.1251F. doi :10.1088/0143-0807/27/5/024. S2CID 16934275.
- Франклин, Джерролд (2008). «Отсутствие вращения в движущемся прямоугольном рычаге». European Journal of Physics . 29 (6): N55–N58. arXiv : 0805.1196 . Bibcode : 2008EJPh...29...55F. doi : 10.1088/0143-0807/29/6/N01. S2CID 118386487.
- Ефименко, Олег Д. (1999). «Парадокс Траутона-Нобла». Journal of Physics A. 32 ( 20): 3755–3762. Bibcode : 1999JPhA...32.3755J. doi : 10.1088/0305-4470/32/20/308. S2CID 5923766.
- Арзельес, Х. (1965). «Sur le problème relativiste du levier coudé». Иль Нуово Чименто . 35 (3): 783–791. Бибкод : 1965NCim...35..783A. дои : 10.1007/BF02739341. S2CID 120383996.
- Рорлих, Ф. (1966). «Истинные и кажущиеся преобразования, классические электроны и релятивистская термодинамика». Il Nuovo Cimento B. 45 ( 1): 76–83. Bibcode : 1966NCimB..45...76R. doi : 10.1007/BF02710587. S2CID 123061629.
- Ньюбург, РГ (1969). «Релятивистская проблема прямоугольного рычага: правильность решения Лауэ». Il Nuovo Cimento B. 61 ( 2): 201–209. Bibcode : 1969NCimB..61..201N. doi : 10.1007/BF02710928. S2CID 117911369.
- Каваллери, Дж.; Сальгарелли, Дж. (1969). «Пересмотр релятивистской динамики с переменной массой покоя и применение к релятивистской термодинамике». Il Nuovo Cimento A. 62 ( 3): 722–754. Bibcode : 1969NCimA..62..722C. doi : 10.1007/BF02819595. S2CID 124525672.
- Аранофф, С. (1972). "Равновесие в специальной теории относительности" (PDF) . Il Nuovo Cimento B . 10 (1): 155–171. Bibcode :1972NCimB..10..155A. doi :10.1007/BF02911417. S2CID 117291369. Архивировано из оригинала (PDF) 2012-03-28.
- Грён, О. (1973). «Асинхронная формулировка релятивистской статики и термодинамики». Il Nuovo Cimento B. 17 ( 1): 141–165. Bibcode : 1973NCimB..17..141G. doi : 10.1007/BF02906436. S2CID 122454306.
- Pahor, S.; Strnad, J. (1974). «Статика в специальной теории относительности». Il Nuovo Cimento B. 20 ( 1): 105–112. Bibcode : 1974NCimB..20..105P. doi : 10.1007/BF02721111. S2CID 123433408.
- Каваллери, Г.; Спавиери, Г.; Спинелли, Г. (1975). «Веревки и блоки в специальной теории относительности (релятивистская статика нитей)». Иль Нуово Чименто Б. 25 (1): 348–356. Бибкод : 1975NCimB..25..348C. дои : 10.1007/BF02737685. S2CID 120491330.
- Чаморро, А.; Эрнандес, А. (1978). «Синхронная формулировка релятивистской статики». Il Nuovo Cimento B. 41 ( 1): 236–244. Bibcode : 1977NCimB..41..236C. doi : 10.1007/BF02726555. S2CID 118140054.
- Эрнандес, А.; Ривас, М.; Агиррегабирия, Дж. М. (1982). «Количественный анализ эксперимента с фортоном-ноблом». Иль Нуово Чименто Б. 72 (1): 1–12. Бибкод : 1982NCimB..72....1H. дои : 10.1007/BF02894929. S2CID 118263084.
- Ай, Сяо-Бай (1993). «Историческое заблуждение в релятивистской статике». Иль Нуово Чименто Б. 108 (1): 7–15. Бибкод : 1993NCimB.108....7A. дои : 10.1007/BF02874335. S2CID 120591882.
- Ниевес, Л.; Родригес, М.; Спавьери, Г.; Тонни, Э. (2001). «Эксперимент типа Траутона-Нобла как проверка дифференциальной формы закона Фарадея». Il Nuovo Cimento B. 116 ( 5): 585. Bibcode : 2001NCimB.116..585N.
- Спавьери, Г.; Джиллис, Г.Т. (2003). "Фундаментальные тесты электродинамических теорий: Концептуальные исследования эффектов Траутона-Нобла и скрытого импульса". Il Nuovo Cimento B. 118 ( 3): 205. Bibcode : 2003NCimB.118..205S.
- Проховник, С. Й.; Ковач, КП (1985). «Применение специальной теории относительности к прямоугольному рычагу». Основы физики . 15 (2): 167–173. Bibcode :1985FoPh...15..167P. doi :10.1007/BF00735288. S2CID 120649126.
- Спавьери, Джанфранко (1990). «Предложение об экспериментах по обнаружению недостающего момента в специальной теории относительности». Foundations of Physics Letters . 3 (3): 291–302. Bibcode : 1990FoPhL...3..291S. doi : 10.1007/BF00666019. S2CID 122236005.
- Ивезич, Томислав (2005). «Аксиоматическая геометрическая формулировка электромагнетизма с одной аксиомой: уравнение поля для бивекторного поля F с объяснением эксперимента Троутона-Нобла». Foundations of Physics Letters . 18 (5): 401–429. arXiv : physics/0412167 . Bibcode : 2005FoPhL..18..401I. doi : 10.1007/s10702-005-7533-7. S2CID 6907453.
- Ивезич, Томислав (2006). «Четырехмерные геометрические величины против обычных трехмерных величин: разрешение парадокса Джексона». Основы физики . 36 (10): 1511–1534. arXiv : physics/0602105 . Bibcode :2006FoPh...36.1511I. doi :10.1007/s10701-006-9071-y. S2CID 17410595.
- Ивезич, Томислав (2006). «Повторный парадокс Троутона Нобла». Основы физики . 37 (4–5): 747–760. arXiv : physics/0606176 . Bibcode :2007FoPh...37..747I. doi :10.1007/s10701-007-9116-x. S2CID 5977062.
Внешние ссылки
- Кевин Браун, «Траутон-Нобл и прямоугольный рычаг» на MathPages.
- Мишель Янссен, «Эксперимент Траутона и E = mc2», архив 17 октября 2015 г. на Wayback Machine , курс «Эйнштейн для всех » в UMN (2002).























![{\displaystyle {\frac {d{\bf {p}}}{dt}}=m{\frac {d}{dt}}({\bf {v}}\gamma )=m\gamma ^{3}[{\bf {a}}+{\bf {v\times (v\times a)}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d25b24e18a2ccd119749de70f85cb33629905f2)