Тридекагон

Правильный тридекагон
Правильный тридекагон
Тип	Правильный многоугольник
Ребра и вершины	13
Символ Шлефли	{13}
Диаграммы Кокстера–Дынкина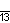
Группа симметрии	Двугранный (D 13 ), порядок 2×13
Внутренний угол ( градусы )	≈152.308°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии тридекагон , трискайдекагон или 13-угольник — это многоугольник с тринадцатью сторонами .

Правильный тридекагон обозначается символом Шлефли {13} .

Величина каждого внутреннего угла правильного тридекагона составляет приблизительно 152,308 градуса , а площадь со стороной длиной a определяется по формуле

${\displaystyle A={\frac {13}{4}}a^{2}\cot {\frac {\pi }{13}}\simeq 13.1858\,a^{2}.}$

Поскольку 13 является простым числом Пьерпонта , но не простым числом Ферма , правильный тридекагон не может быть построен с помощью циркуля и линейки . Однако его можно построить с помощью неусиса , или трисектора угла.

Ниже представлена ​​анимация построения правильного тридекагона с радиусом описанной окружности по методу Эндрю М. Глисона ^[1], основанная на трисекции угла с помощью томагавка (светло-голубого).${\displaystyle {\overline {ОА}}=12,}$

Здесь показано приблизительное построение правильного тридекагона с использованием линейки и циркуля .

Еще одна возможная анимация приблизительного построения, также возможная с использованием линейки и циркуля.

• Построенная длина стороны в GeoGebra ${\displaystyle a=0.478631328575115\;[{\text{единица длины}}]}$
• Длина стороны тридекагона${\displaystyle a_{\text{target}}=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)=0.478631328575115\ldots \;[{\text{unit of length}}]}$
• Абсолютная погрешность построенной длины стороны:

До максимальной точности в 15 знаков после запятой абсолютная погрешность составляет${\displaystyle F_{a}=a-a_{\text{target}}=0.0\;[{\text{unit of length}}]}$

• Построен центральный угол тридекагона в GeoGebra (отображение значимых 13 знаков после запятой, округлено)${\displaystyle \mu =27.6923076923077^{\circ }}$
• Центральный угол тридекагона${\displaystyle \mu _{\text{target}}=\left({\frac {360^{\circ }}{13}}\right)=27.{\overline {692307}}^{\circ }}$
• Абсолютная угловая погрешность построенного центрального угла:

До 13 знаков после запятой абсолютная погрешность составляет${\displaystyle F_{\mu }=\mu -\mu _{\text{target}}=0.0^{\circ }}$

При описании окружности радиусом r = 1 млрд км (расстояние, которое свет проходит примерно за 55 минут) абсолютная погрешность определения длины стороны составит менее 1 мм.

Правильный тридекагон имеет симметрию Dih ₁₃ порядка 26. Поскольку 13 — простое число, то существует одна подгруппа с диэдральной симметрией: Dih ₁ и 2 циклические группы симметрии: Z ₁₃ и Z ₁ .

Эти 4 симметрии можно увидеть в 4 различных симметриях на тридекагоне. Джон Конвей обозначает их буквой и порядком группы. ^[2] Полная симметрия правильной формы — r26 , и ни одна симметрия не обозначена как a1 . Диэдральные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены как g для их центрального порядка инерции.

Каждая подгруппа симметрии допускает одну или несколько степеней свободы для нерегулярных форм. Только подгруппа g13 не имеет степеней свободы, но может рассматриваться как направленные ребра .

Правильный тридекагон используется в качестве формы чешской монеты достоинством 20 крон . ^[3]

Тридекаграмма — это 13-сторонний звездчатый многоугольник . Существует 5 правильных форм, заданных символами Шлефли : {13/2}, {13/3}, {13/4}, {13/5} и {13/6}. Поскольку 13 — простое число, ни одна из тридекаграмм не является составной фигурой. В культурном отношении эта форма является символом бессмертия .

Тридекаграммы
Картина	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
Внутренний угол	≈124.615°	≈96.9231°	≈69.2308°	≈41.5385°	≈13.8462°

Правильный тридекагон — это многоугольник Петри 12-симплекс :

А 12
12-симплекс

• Вайсштейн, Эрик В. «Тридекагон». MathWorld .