Поперечная проекция Меркатора

Поперечная картографическая проекция Меркатора ( TM , TMP ) является адаптацией стандартной проекции Меркатора . Поперечная версия широко используется в национальных и международных картографических системах по всему миру, включая универсальную поперечную проекцию Меркатора . В сочетании с подходящим геодезическим датумом поперечная проекция Меркатора обеспечивает высокую точность в зонах менее нескольких градусов в направлении с востока на запад.

Поперечная проекция Меркатора является поперечным аспектом стандартной (или нормальной ) проекции Меркатора. Они имеют одну и ту же базовую математическую конструкцию, и, следовательно, поперечная проекция Меркатора наследует многие черты от нормальной проекции Меркатора:

• Обе проекции являются цилиндрическими : для нормальной проекции Меркатора ось цилиндра совпадает с полярной осью, а линия касания — с экватором. Для поперечной проекции Меркатора ось цилиндра лежит в экваториальной плоскости, а линия касания — любой выбранный меридиан, тем самым обозначаемый как центральный меридиан .
• Обе проекции могут быть преобразованы в секущие формы, что означает уменьшение масштаба таким образом, чтобы цилиндр пересекал модельный глобус.
• Оба существуют в сферической и эллипсоидальной формах.
• Обе проекции являются конформными , так что масштаб точки не зависит от направления, а локальные формы хорошо сохраняются;
• Обе проекции имеют постоянный масштаб на линии касания (экватор для нормальной проекции Меркатора и центральный меридиан для поперечной).

Поскольку центральный меридиан поперечной проекции Меркатора может быть выбран по желанию, его можно использовать для построения высокоточных карт (узкой ширины) в любой точке земного шара. Секущая, эллипсоидальная форма поперечной проекции Меркатора является наиболее широко применяемой из всех проекций для точных крупномасштабных карт.

При построении карты в любой проекции сфера обычно выбирается для моделирования Земли, когда протяженность отображаемой области превышает несколько сотен километров в длину в обоих измерениях. Для карт меньших областей следует выбирать эллипсоидальную модель , если требуется большая точность; см. следующий раздел. Сферическая форма поперечной проекции Меркатора была одной из семи новых проекций, представленных в 1772 году Иоганном Генрихом Ламбертом . ^{[1] [2]} (Текст также доступен в современном английском переводе. ^[3] ) Ламберт не давал названия своим проекциям; название поперечная Меркатор датируется второй половиной девятнадцатого века. ^[4] Основные свойства поперечной проекции здесь представлены в сравнении со свойствами нормальной проекции.

	Нормальная проекция Меркатора			Поперечная проекция Меркатора
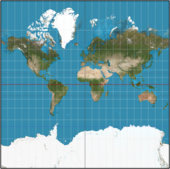•	Центральный меридиан проецируется на прямую линию x  = 0. Остальные меридианы проецируются на прямые линии с  постоянным x .		•	Центральный меридиан проецируется на прямую линию x  = 0. Меридианы, расположенные на 90 градусов к востоку и западу от центрального меридиана, проецируются на линии постоянного  y, проходящие через проецируемые полюса. Все остальные меридианы проецируются на сложные кривые.
•	Экватор проецируется на прямую линию y  = 0, а параллельные окружности проецируются на прямые линии постоянного  y .		•	Экватор проецируется на прямую линию y  = 0, но все остальные параллели представляют собой сложные замкнутые кривые.
•	Спроецированные меридианы и параллели пересекаются под прямым углом.		•	Спроецированные меридианы и параллели пересекаются под прямым углом.
•	Проекция неограничена в направлении Y. Полюса лежат в бесконечности.		•	Проекция не ограничена в направлении x . Точки на экваторе, расположенные под углом девяносто градусов к центральному меридиану, проецируются в бесконечность.
•	Проекция равноугольная. Формы мелких элементов хорошо сохранились.		•	Проекция равноугольная. Формы мелких элементов хорошо сохранились.
•	Искажение увеличивается с  y . Проекция не подходит для карт мира. Искажение мало вблизи экватора, и проекция (особенно в ее эллипсоидальной форме) подходит для точного картографирования экваториальных регионов.		•	Искажение увеличивается с  x . Проекция не подходит для карт мира. Искажение мало вблизи центрального меридиана, и проекция (особенно в ее эллипсоидальной форме) подходит для точного картографирования узких регионов.
•	Гренландия почти такая же большая, как Африка; ее фактическая площадь составляет примерно одну четырнадцатую площади Африки.		•	Когда Гренландия и Африка находятся вблизи центрального меридиана, их формы точны, а соотношение площадей является хорошим приближением к фактическим значениям.
•	Коэффициент масштабирования точки не зависит от направления. Он является функцией  y на проекции. (На сфере он зависит только от широты.) Масштаб верен на экваторе.		•	Коэффициент масштабирования точки не зависит от направления. Он является функцией x на проекции. (На сфере он зависит как от широты, так и от долготы.) Масштаб верен на центральном меридиане.
•	Проекция достаточно точна вблизи экватора. Масштаб на угловом расстоянии 5° (по широте) от экватора меньше, чем на 0,4% больше масштаба на экваторе, и примерно на 1,54% больше на угловом расстоянии 10°.		•	Проекция достаточно точна вблизи центрального меридиана. Масштаб на угловом расстоянии 5° (по долготе) от центрального меридиана меньше, чем на 0,4% больше масштаба на центральном меридиане, и составляет около 1,54% на угловом расстоянии 10°.
•	В секущей версии масштаб уменьшен на экваторе и он верен на двух линиях, параллельных проецируемому экватору (и соответствующих двум параллельным окружностям на сфере).		•	В секущей версии масштаб уменьшен на центральном меридиане, и он верен на двух линиях, параллельных проецируемому центральному меридиану. (Эти две линии не являются меридианами.)
•	Конвергенция (угол между проецируемыми меридианами и линиями сетки с постоянной x ) тождественно равна нулю. Север сетки и истинный север совпадают.		•	Конвергенция равна нулю на экваторе и ненулевая везде. Она увеличивается по мере приближения к полюсам. Север сетки и истинный север не совпадают.
•	Локальные линии (постоянного азимута на сфере) проецируются в прямые линии.

Эллипсоидальная форма поперечной проекции Меркатора была разработана Карлом Фридрихом Гауссом в 1822 году ^[5] и дополнительно проанализирована Иоганном Генрихом Луи Крюгером в 1912 году ^[6].

Проекция известна под несколькими названиями: (эллипсоидальная) поперечная Меркатора в США; Гаусс-конформная или Гаусс-Крюгер в Европе; или Гаусс-Крюгер поперечная Меркатора в более общем смысле. Помимо того, что это просто синоним эллипсоидальной поперечной картографической проекции Меркатора, термин Гаусс-Крюгер может использоваться и в других, немного отличающихся значениях:

• Иногда этот термин используется для конкретного вычислительного метода для поперечной проекции Меркатора: то есть, как преобразовывать широту/долготу и проецируемые координаты. Не существует простой замкнутой формулы для этого, когда Земля моделируется как эллипсоид. Но метод Гаусса–Крюгера дает те же результаты, что и другие методы, по крайней мере, если вы достаточно близки к центральному меридиану: менее 100 градусов долготы, скажем. Дальше некоторые методы становятся неточными.
• Термин также используется для определенного набора поперечных проекций Меркатора, используемых в узких зонах в Европе и Южной Америке, по крайней мере в Германии, Турции, Австрии, Словении, Хорватии, Боснии и Герцеговине, Сербии, Черногории, Северной Македонии, Финляндии и Аргентине. Эта система Гаусса-Крюгера похожа на универсальную поперечную систему Меркатора, но центральные меридианы зон Гаусса-Крюгера находятся всего в 3° друг от друга, в отличие от 6° в UTM.

Проекция является конформной с постоянным масштабом на центральном меридиане. (Существуют и другие конформные обобщения поперечной проекции Меркатора от сферы до эллипсоида, но только проекция Гаусса-Крюгера имеет постоянный масштаб на центральном меридиане.) На протяжении двадцатого века поперечная проекция Меркатора Гаусса-Крюгера была принята в той или иной форме многими странами (и международными организациями); ^[7] кроме того, она обеспечивает основу для серии проекций Universal Transverse Mercator . Проекция Гаусса-Крюгера в настоящее время является наиболее широко используемой проекцией в точном крупномасштабном картографировании. ^{[ требуется ссылка ]}

Проекция, разработанная Гауссом и Крюгером, была выражена в терминах степенных рядов низкого порядка , которые, как предполагалось, расходятся в направлении восток-запад, точно так же, как в сферической версии. Это было доказано британским картографом Э. Х. Томпсоном, чья неопубликованная точная (замкнутая форма) версия проекции, сообщенная Лоуренсом Патриком Ли в 1976 году, ^[8] показала, что эллипсоидальная проекция конечна (ниже). Это самое поразительное различие между сферической и эллипсоидальной версиями поперечной проекции Меркатора: Гаусс-Крюгер дает разумную проекцию всего эллипсоида на плоскость, хотя ее основное применение заключается в точном крупномасштабном картографировании «вблизи» центрального меридиана. ^{[ требуется ссылка ]}

• Вблизи центрального меридиана (Гринвич в приведенном выше примере) проекция имеет малое искажение, и формы Африки, Западной Европы, Британских островов, Гренландии и Антарктиды выгодно отличаются от глобусов.
• Центральные области поперечных проекций на сфере и эллипсоиде неразличимы на мелкомасштабных проекциях, показанных здесь.
• Меридианы на 90° к востоку и западу от выбранного центрального меридиана проецируются на горизонтальные линии через полюса. Более отдаленное полушарие проецируется выше северного полюса и ниже южного полюса.
• Экватор делит пополам Африку, пересекает Южную Америку и затем продолжается до полной внешней границы проекции; верхний и нижний края, а также правый и левый края должны быть идентифицированы (т.е. они представляют собой одни и те же линии на земном шаре). (Индонезия разделена пополам.)
• Искажение увеличивается к правой и левой границам проекции, но не увеличивается до бесконечности. Обратите внимание на Галапагосские острова, где 90° западного меридиана встречается с экватором внизу слева.
• Карта является конформной. Линии, пересекающиеся под любым заданным углом на эллипсоиде, проецируются в линии, пересекающиеся под тем же углом на проекции. В частности, параллели и меридианы пересекаются под углом 90°.
• Фактор масштабирования точки не зависит от направления в любой точке, так что форма небольшой области достаточно хорошо сохраняется. Необходимым условием является то, что величина фактора масштабирования не должна слишком сильно меняться в рассматриваемой области. Обратите внимание, что в то время как Южная Америка сильно искажена, остров Цейлон достаточно мал, чтобы иметь разумную форму, хотя он и находится далеко от центрального меридиана.
• Выбор центрального меридиана сильно влияет на вид проекции. Если выбрано 90°W, то вся Америка приемлема. Если выбрано 145°E, то Дальний Восток хорош, а Австралия ориентирована севером вверх.

В большинстве приложений система координат Гаусса–Крюгера применяется к узкой полосе вблизи центральных меридианов, где различия между сферической и эллипсоидальной версиями невелики, но тем не менее важны для точного картографирования. Прямые ряды для масштаба, конвергенции и искажения являются функциями эксцентриситета и как широты, так и долготы на эллипсоиде: обратные ряды являются функциями эксцентриситета и как x, так и y на проекции. В секущей версии линии истинного масштаба на проекции больше не параллельны центральному меридиану; они слегка искривлены. Угол конвергенции между спроецированными меридианами и линиями сетки константы x больше не равен нулю (за исключением экватора), поэтому необходимо скорректировать пеленг сетки, чтобы получить азимут от истинного севера. Разница невелика, но ею нельзя пренебрегать, особенно на высоких широтах.

В своей статье 1912 года ^[6] Крюгер представил два различных решения, различающихся здесь параметром расширения:

• Крюгер– n (пункты 5–8): Формулы для прямой проекции, дающие координаты x и y , являются разложениями четвертого порядка относительно третьего сплющивания n (отношение разности и суммы большой и малой осей эллипсоида). Коэффициенты выражены через широту ( φ ), долготу ( λ ), большую ось ( a ) и эксцентриситет ( e ). Обратные формулы для φ и λ также являются разложениями четвертого порядка относительно n, но с коэффициентами, выраженными через x , y , a и e .
• Крюгера– λ (пункты 13 и 14): Формулы, задающие координаты проекции x и y, являются разложениями (порядков 5 и 4 соответственно) по долготе λ , выраженной в радианах: коэффициенты выражаются через φ , a и e . Обратная проекция для φ и λ является разложением шестого порядка по отношению ⁠х/а⁠ , с коэффициентами, выраженными через y , a и e . (См. Поперечная проекция Меркатора: серия Редферна .)

Ряды Крюгера– λ были реализованы первыми, возможно, потому, что их было гораздо легче оценивать на ручных калькуляторах середины двадцатого века.

• Ли–Редфирн–ОСГБ : В 1945 году Л. П. Ли ^[9] подтвердил λ- расширения Крюгера и предложил их принятие OSGB ^[10], но Редфирн (1948) ^[11] указал, что они неточны из-за (a) относительно высоких широт Великобритании и (b) большой ширины картографируемой области, более 10 градусов долготы. Редфирн расширил ряд до восьмого порядка и рассмотрел, какие члены необходимы для достижения точности 1 мм (наземное измерение). Ряды Редфирна по-прежнему являются основой картографических проекций OSGB. ^[10]
• Thomas–UTM : λ- расширения Крюгера были также подтверждены Полом Томасом в 1952 году: ^[12] они легко доступны у Снайдера. ^[13] Его проекционные формулы, полностью эквивалентные представленным Редферном, были приняты Агентством по картографии Министерства обороны США в качестве основы для UTM . ^[14] Они также включены в преобразователь координат GEOTRANS ^[15] , предоставленный Управлением геоматики Национального агентства геопространственной разведки США.
• Другие страны : Серия Redfearn является основой для геодезического картографирования во многих странах: Австралия, Германия, Канада, Южная Африка и многие другие. (Список приведен в Приложении A.1 Stuifbergen 2009.) ^[16]
• Было предложено много вариантов серии Редфирна, но только те, которые были приняты национальными картографическими агентствами, имеют значение. Пример модификаций, не имеющих такого статуса, см. в разделе Поперечная проекция Меркатора: серия Боуринга . Все такие модификации были затмены мощью современных компьютеров и развитием n -серий высокого порядка, описанных ниже. Точные серии Редфирна, хотя и низкого порядка, нельзя игнорировать, поскольку они все еще закреплены в квазилегальных определениях OSGB и UTM и т. д.

Ряд Крюгера– n был реализован (до четвертого порядка по n ) следующими странами.

• Франция ^[17]
• Финляндия ^[18]
• Швеция ^[19]
• Япония ^[20]

Версии ряда Крюгера –n более высокого порядка были реализованы до седьмого порядка Энгзагером и Подером ^[21] и до десятого порядка Кавасе. ^[22] Помимо расширения ряда для преобразования между широтой и конформной широтой, Карни реализовал ряд до тридцатого порядка. ^[23]

Точное решение EH Thompson описано LP Lee. ^[8] Оно построено в терминах эллиптических функций (определенных в главах 19 и 22 справочника NIST ^[24] ), которые могут быть вычислены с произвольной точностью с использованием алгебраических вычислительных систем, таких как Maxima. ^[25] Такая реализация точного решения описана Karney (2011). ^{[23] [26]}

Точное решение является ценным инструментом для оценки точности усеченных рядов n и λ. Например, исходный ряд Krüger– n 1912 года очень выгодно отличается от точных значений: они отличаются менее чем на 0,31 мкм в пределах 1000 км от центрального меридиана и менее чем на 1 мм к 6000 км. С другой стороны, разница между рядом Redfearn, используемым GEOTRANS, и точным решением составляет менее 1 мм к разнице долготы в 3 градуса, что соответствует расстоянию 334 км от центрального меридиана на экваторе, но всего лишь 35 км на северной границе зоны UTM. Таким образом, ряд Krüger– n намного лучше ряда Redfearn λ.

Серия Редфирна становится намного хуже по мере расширения зоны. Карни рассматривает Гренландию как поучительный пример. Длинный тонкий массив суши сосредоточен на 42W и в самой широкой точке находится не более чем в 750 км от этого меридиана, в то время как размах по долготе достигает почти 50 градусов. Крюгер– n имеет точность в пределах 1 мм, но версия Редфирна серии Крюгера– λ имеет максимальную ошибку в 1 километр.

Ряд Карни 8-го порядка (по n ) имеет точность до 5 морских миль в пределах 3900 км от центрального меридиана.

Нормальные цилиндрические проекции описываются относительно цилиндра, касательного к экватору с осью вдоль полярной оси сферы. Цилиндрические проекции строятся так, что все точки на меридиане проецируются в точки с (где — радиус Земли ), а — предписанная функция . Для касательной нормальной проекции Меркатора (единственные) формулы, гарантирующие конформность, следующие: ^[27]${\displaystyle x=a\лямбда}$${\displaystyle а}$${\displaystyle у}$${\displaystyle \фи}$

${\displaystyle x=a\lambda \,,\qquad y=a\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right]={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right].}$

Конформность подразумевает, что точечный масштаб k не зависит от направления: он является функцией только широты:

${\displaystyle k(\varphi)=\sec \varphi .\,}$

Для секущей версии проекции в правой части всех этих уравнений имеется множитель k ₀ : это гарантирует, что масштаб на экваторе равен k _{0 .}

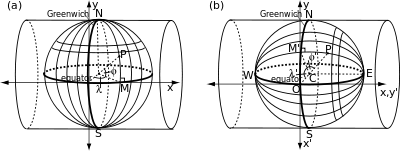
Рисунок слева показывает, как поперечный цилиндр связан с обычной сеткой на сфере. Он касается некоторого произвольно выбранного меридиана, а его ось перпендикулярна оси сферы. Оси x и y , определенные на рисунке, связаны с экватором и центральным меридианом точно так же, как для нормальной проекции. На рисунке справа повернутая сетка связана с поперечным цилиндром таким же образом, как нормальный цилиндр связан со стандартной сеткой. «Экватор», «полюса» (E и W) и «меридианы» повернутой сетки отождествляются с выбранным центральным меридианом, точками на экваторе в 90 градусах к востоку и западу от центрального меридиана и большими окружностями, проходящими через эти точки.

Положение произвольной точки ( φ , λ ) на стандартной сетке также можно определить в терминах углов на повернутой сетке: φ′ (угол M′CP) является эффективной широтой, а − λ′ (угол M′CO) становится эффективной долготой. (Знак минус необходим для того, чтобы ( φ′ , λ′ ) были связаны с повернутой сеткой так же, как ( φ , λ ) связаны со стандартной сеткой). Декартовы оси ( x′ , y′ ) связаны с повернутой сеткой так же, как оси ( x , y ) связаны со стандартной сеткой.

Касательная поперечная проекция Меркатора определяет координаты ( x′ , y′ ) через − λ′ и φ′ с помощью формул преобразования касательной нормальной проекции Меркатора:

${\displaystyle x'=-a\lambda '\,\qquad y'={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi '}{1-\sin \varphi '}}\right].}$

Это преобразование проецирует центральный меридиан на прямую линию конечной длины и в то же время проецирует большие окружности через E и W (включая экватор) на бесконечные прямые линии, перпендикулярные центральному меридиану. Истинные параллели и меридианы (кроме экватора и центрального меридиана) не имеют простого отношения к повернутой сетке и проецируются на сложные кривые.

Углы двух сеток связаны с помощью сферической тригонометрии на сферическом треугольнике NM′P, определяемом истинным меридианом через начало координат, OM′N, истинным меридианом через произвольную точку, MPN, и большим кругом WM′PE. Результаты таковы: ^[27]

${\displaystyle {\begin{aligned}\sin \varphi '&=\sin \lambda \cos \varphi, \\\tan \lambda '&=\sec \lambda \tan \varphi .\end{aligned}}}$

Прямые формулы, дающие декартовы координаты ( x , y ), немедленно следуют из вышеизложенного. Принимая x  =  y′ и y  = − x′ (и восстанавливая множители k ₀ для учета версий секущей)

${\displaystyle {\begin{aligned}x(\lambda,\varphi)&={\frac {1}{2}}k_{0}a\ln \left[{\frac {1+\sin \lambda \ cos \varphi }{1-\sin \lambda \cos \varphi }}\right],\\[5px]y(\lambda ,\varphi )&=k_{0}a\arctan \left[\sec \lambda \tan \varphi \right],\end{aligned}}}$

Вышеуказанные выражения приведены в работе Ламберта ^[1] , а также (без выводов) в работах Снайдера ^[13] , Мэлинга ^[28] и Осборна ^[27] (с полными подробностями).

Обращение приведенных выше уравнений дает

${\displaystyle {\begin{aligned}\lambda (x,y)&=\arctan \left[\sinh {\frac {x}{k_{0}a}}\sec {\frac {y}{k_{0}a}}\right],\\[5px]\varphi (x,y)&=\arcsin \left[{\mbox{sech}}\;{\frac {x}{k_{0}a}}\sin {\frac {y}{k_{0}a}}\right].\end{aligned}}}$

В терминах координат относительно повернутой сетки коэффициент масштабирования точек определяется как k  = sec  φ′ : он может быть выражен либо в терминах географических координат, либо в терминах координат проекции:

${\displaystyle {\begin{aligned}k(\lambda ,\varphi )&={\frac {k_{0}}{\sqrt {1-\sin ^{2}\lambda \cos ^{2}\varphi }}},\\[5px]k(x,y)&=k_{0}\cosh \left({\frac {x}{k_{0}a}}\right).\end{aligned}}}$

Второе выражение показывает, что масштабный фактор является просто функцией расстояния от центрального меридиана проекции. Типичное значение масштабного фактора равно k ₀  = 0,9996, так что k  = 1, когда x составляет приблизительно 180 км. Когда x составляет приблизительно 255 км и k ₀  = 1,0004: масштабный фактор находится в пределах 0,04% от единицы на полосе шириной около 510 км.

Угол конвергенции γ в точке проекции определяется углом, измеренным от проецируемого меридиана, который определяет истинный север, до линии сетки постоянной x , определяющей север сетки. Таким образом, γ положительно в квадранте к северу от экватора и к востоку от центрального меридиана, а также в квадранте к югу от экватора и к западу от центрального меридиана. Конвергенция должна быть добавлена ​​к пеленгу сетки, чтобы получить пеленг от истинного севера. Для секущей поперечной проекции Меркатора конвергенция может быть выражена ^[27] либо в терминах географических координат, либо в терминах координат проекции:

${\displaystyle {\begin{aligned}\gamma (\lambda ,\varphi )&=\arctan(\tan \lambda \sin \varphi ),\\[5px]\gamma (x,y)&=\arctan \left(\tanh {\frac {x}{k_{0}a}}\tan {\frac {y}{k_{0}a}}\right).\end{aligned}}}$

Подробности фактических реализаций

• Ряд Гаусса-Крюгера в долготе: Поперечная проекция Меркатора: Ряд Редферна
• Ряд Гаусса-Крюгера в n (третье сжатие): Поперечная проекция Меркатора: ряд сжатий
• Точная (замкнутая форма) поперечная проекция Меркатора: Поперечная проекция Меркатора: точное решение
• Ряд Редферна четвертого порядка по кратким формулам (пример): Поперечная проекция Меркатора: Ряд Боуринга

Координаты проекции, полученные в результате различных разработок эллипсоидальной поперечной проекции Меркатора, являются декартовыми координатами, такими, что центральный меридиан соответствует оси x , а экватор соответствует оси y . Как x, так и y определены для всех значений λ и ϕ . Проекция не определяет сетку: сетка является независимой конструкцией, которая может быть определена произвольно. На практике национальные реализации и UTM используют сетки, выровненные с декартовыми осями проекции, но они имеют конечную протяженность, с началами, которые не обязательно совпадают с пересечением центрального меридиана с экватором.

Истинное начало координат сетки всегда берется на центральном меридиане, так что координаты сетки будут отрицательными к западу от центрального меридиана. Чтобы избежать таких отрицательных координат сетки, стандартная практика определяет ложное начало координат к западу (и, возможно, к северу или югу) от начала координат сетки: координаты относительно ложного начала координат определяют восточное и северное направления , которые всегда будут положительными. Ложное восточное направление , E ₀ , является расстоянием истинного начала координат сетки к востоку от ложного начала координат. Ложное северное направление , N ₀ , является расстоянием истинного начала координат сетки к северу от ложного начала координат. Если истинное начало координат сетки находится на широте φ ₀ на центральном меридиане, а масштабный коэффициент центрального меридиана равен k _0, то эти определения дают восточное и северное направления следующим образом:

${\displaystyle {\begin{aligned}E&=E_{0}+x(\lambda ,\varphi ),\\[5px]N&=N_{0}+y(\lambda ,\varphi )-k_{0}m(\varphi _{0}).\end{aligned}}}$

Термины «восток» и «север» не означают строго восточное и северное направления. Линии сетки поперечной проекции, кроме осей x и y , не проходят с севера на юг или с востока на запад, как это определено параллелями и меридианами. Это очевидно из глобальных проекций, показанных выше. Вблизи центрального меридиана различия невелики, но измеримы. Разница между линиями сетки север-юг и истинными меридианами — это угол конвергенции.

• Список картографических проекций
• проекция Меркатора
• Масштаб (карта)
• Косая проекция Меркатора

На Викискладе есть медиафайлы по теме «Проекция Меркатора» .

На Викискладе есть медиафайлы по теме Карты с поперечной проекцией Меркатора .

• Проекции, использованные для иллюстрации этой статьи, были подготовлены с использованием Geocart, который доступен на сайте Mapthematics Geocart 3