Теория приливов и отливов

Теория приливов представляет собой применение механики сплошной среды для интерпретации и прогнозирования приливных деформаций планетарных и спутниковых тел, их атмосфер и океанов (особенно океанов Земли) под гравитационной нагрузкой другого астрономического тела или тел (особенно Луны и Солнца ).
История
Астрономия австралийских аборигенов
Народ йолнгу , проживающий на северо-востоке Арнем-Ленда в Северной Территории Австралии, установил связь между Луной и приливами, которую они мифически приписывали тому, что Луна наполняется водой и снова опустошается. [1] [2]
Классическая эпоха
Приливы получили сравнительно мало внимания в цивилизациях вокруг Средиземного моря , поскольку приливы там относительно невелики, а области, которые испытывают приливы, делают это ненадежно. [3] [4] [5] Однако был выдвинут ряд теорий, от сравнения движений с дыханием или кровотоком до теорий, связанных с водоворотами или речными циклами. [4] Подобная идея «дышащей земли» рассматривалась некоторыми азиатскими мыслителями. [6] Сообщается, что Платон считал, что приливы были вызваны водой, текущей в подводные пещеры и из них. [3] Кратес из Маллуса приписывал приливы «встречному движению (ἀντισπασμός) моря», а Аполлодор из Керкиры — «отливу из Океана». [7] Древний индийский текст Пураны, датируемый 400–300 гг. до н. э., упоминает подъем и опускание океана из-за теплового расширения от света Луны. [a] [8]
В конечном итоге связь между Луной (и Солнцем ) и приливами стала известна грекам , хотя точная дата открытия неясна; ссылки на нее встречаются в таких источниках, как Пифей из Массилии в 325 г. до н. э. и «Естественная история» Плиния Старшего в 77 г. н. э. Хотя график приливов и связь с лунными и солнечными движениями были известны, точный механизм, который их связывал, был неясен. [4] Классики Томас Литтл Хит утверждали, что и Пифей, и Посидоний связывали приливы с Луной, «первый напрямую, последний через установление ветров». [7] Сенека упоминает в De Providentia периодическое движение приливов, контролируемое лунной сферой. [9] Эратосфен (III в. до н. э.) и Посидоний (I в. до н. э.) оба создали подробные описания приливов и их связи с фазами Луны , Посидоний в частности проводил длительные наблюдения за морем на испанском побережье, хотя мало что из их работ сохранилось. Влияние Луны на приливы упоминалось в «Тетрабиблосе » Птолемея как доказательство реальности астрологии . [3] [10] Считается, что Селевк из Селевкии выдвинул теорию около 150 г. до н. э. о том, что приливы вызываются Луной, как часть его гелиоцентрической модели. [11] [12]
Аристотель , судя по обсуждениям его убеждений в других источниках, как полагают, считал, что приливы были вызваны ветрами, подгоняемыми жаром Солнца, и он отверг теорию о том, что приливы были вызваны Луной. Апокрифическая легенда утверждает, что он покончил с собой, разочаровавшись в своей неспособности полностью понять приливы. [3] Гераклид также считал, что « солнце создает ветры, и что эти ветры, когда они дуют, вызывают приливы, а когда они прекращаются, — отливы». [7] Дикеарх также «приписывал приливы непосредственному воздействию солнца в соответствии с его положением». [7] Филострат обсуждает приливы в пятой книге « Жизни Аполлония Тианского » (около 217-238 гг. н. э.); он смутно осознавал связь приливов и отливов с фазами Луны, но приписывал их духам, перемещающим воду в пещеры и из них, что он связывал с легендой о том, что духи умерших не могут двигаться дальше при определенных фазах Луны. [b]
Средневековый период
Достопочтенный Беда обсуждает приливы в «Расчете времени» и показывает, что дважды в день время приливов связано с Луной и что лунный ежемесячный цикл весенних и квадратурных приливов также связан с положением Луны. Он продолжает отмечать, что время приливов различается вдоль одного и того же побережья и что движение воды вызывает отлив в одном месте, когда в другом месте прилив. [13] Однако он не продвинулся в вопросе о том, как именно Луна создает приливы. [4]
Средневековые эмпирические методы прогнозирования приливов, как говорят, позволяли «узнать, что Луна делает высокую воду» по ее движениям. [14] Данте упоминает влияние Луны на приливы в своей «Божественной комедии» . [15] [3]
Средневековое европейское понимание приливов часто основывалось на трудах мусульманских астрономов , которые стали доступны благодаря латинскому переводу, начиная с XII века. [16] Абу Машар аль-Балхи в своем труде Introductorium in astronomiam учил, что приливы и отливы вызываются Луной. [16] Абу Машар обсуждал влияние ветра и фаз Луны относительно Солнца на приливы. [16] В XII веке аль-Битруджи внес вклад в идею о том, что приливы вызываются общей циркуляцией небес. [16] Средневековые арабские астрологи часто ссылались на влияние Луны на приливы как на доказательство реальности астрологии; некоторые из их трактатов по этой теме оказали влияние на Западную Европу. [10] [3] Некоторые предполагали, что влияние было вызвано лунными лучами, нагревающими дно океана. [5]
Современная эпоха
Симон Стевин в своей работе 1608 года «Теория приливов и отливов » опровергает большое количество заблуждений, которые все еще существовали относительно приливов и отливов. Стевин отстаивает идею о том, что притяжение Луны ответственно за приливы, и пишет в ясных терминах об отливах, приливах, весенних приливах и квадратурных приливах, подчеркивая необходимость проведения дальнейших исследований. [17] [18] В 1609 году Иоганн Кеплер справедливо предположил, что гравитация Луны вызывает приливы, [c] которые он сравнивал с магнитным притяжением [20] [4] [21] [22], основывая свои аргументы на древних наблюдениях и корреляциях.
В 1616 году Галилео Галилей написал «Рассуждение о приливах» . [23] Он решительно и насмешливо отвергает лунную теорию приливов, [21] [4] и пытается объяснить приливы как результат вращения Земли и обращения вокруг Солнца , полагая, что океаны движутся, как вода в большом бассейне: как движется бассейн, так движется и вода. [24] Поэтому, когда Земля вращается, сила вращения Земли заставляет океаны «попеременно ускоряться и замедляться». [25] Его взгляд на колебание и «попеременно ускоряющееся и замедляющееся» движение вращения Земли является «динамическим процессом», который отклоняется от предыдущей догмы, которая предполагала «процесс расширения и сжатия морской воды». [26] Однако теория Галилея была ошибочной. [23] В последующие столетия дальнейший анализ привел к современной приливной физике. Галилей пытался использовать свою приливную теорию, чтобы доказать движение Земли вокруг Солнца. Галилей предположил, что из-за движения Земли границы океанов, таких как Атлантический и Тихий, будут показывать один прилив и один отлив в день. Средиземное море имело два прилива и отлива, хотя Галилей утверждал, что это было результатом вторичных эффектов и что его теория будет верна в Атлантике. Однако современники Галилея отмечали, что в Атлантике также было два прилива и отлива в день, что привело к тому, что Галилей исключил это утверждение из своего Диалога 1632 года . [27]
Рене Декарт предположил, что приливы (наряду с движением планет и т. д.) были вызваны эфирными вихрями , без ссылки на теории гравитации Кеплера путем взаимного притяжения; это было чрезвычайно влиятельно, и многочисленные последователи Декарта излагали эту теорию на протяжении всего 17 века, особенно во Франции. [28] Однако Декарт и его последователи признавали влияние Луны, предполагая, что волны давления от Луны через эфир были ответственны за корреляцию. [5] [29] [6] [30]

Ньютон в «Началах » дает правильное объяснение приливной силы , которое можно использовать для объяснения приливов на планете, покрытой однородным океаном, но которое не учитывает распределение континентов или батиметрию океана . [31]
Динамическая теория
В то время как Ньютон объяснял приливы, описывая силы, порождающие приливы, а Даниил Бернулли дал описание статической реакции вод на Земле на приливной потенциал, динамическая теория приливов , разработанная Пьером-Симоном Лапласом в 1775 году, [32] описывает реальную реакцию океана на приливные силы. [33] Теория океанских приливов Лапласа учитывает трение , резонанс и естественные периоды океанических бассейнов. Она предсказывает крупные амфидромические системы в мировых океанических бассейнах и объясняет океанические приливы, которые фактически наблюдаются. [34]
Теория равновесия, основанная на гравитационном градиенте от Солнца и Луны, но игнорирующая вращение Земли, влияние континентов и другие важные эффекты, не могла объяснить реальные океанские приливы. [35] Поскольку измерения подтвердили динамическую теорию, многие вещи теперь имеют возможные объяснения, например, как приливы взаимодействуют с глубоководными хребтами, а цепи подводных гор вызывают глубокие водовороты, которые переносят питательные вещества из глубины на поверхность. [36] Теория равновесных приливов вычисляет высоту приливной волны менее полуметра, в то время как динамическая теория объясняет, почему приливы достигают 15 метров. [37]
Спутниковые наблюдения подтверждают точность динамической теории, и приливы во всем мире теперь измеряются с точностью до нескольких сантиметров. [38] [39] Измерения со спутника CHAMP близко соответствуют моделям, основанным на данных TOPEX . [40] [41] [42] Точные модели приливов во всем мире необходимы для исследований, поскольку изменения, вызванные приливами, должны быть удалены из измерений при расчете гравитации и изменений уровня моря. [43]
Приливные уравнения Лапласа
В 1776 году Лаплас сформулировал единый набор линейных уравнений в частных производных для приливного течения, описанного как баротропный двумерный поток. Введены эффекты Кориолиса , а также боковое воздействие гравитации . Лаплас получил эти уравнения, упростив уравнения динамики жидкости , но их также можно вывести из интегралов энергии с помощью уравнения Лагранжа .
Для жидкого слоя средней толщины D вертикальная приливная высота ζ , а также горизонтальные компоненты скорости u и v (в направлениях широты φ и долготы λ соответственно) удовлетворяют приливным уравнениям Лапласа : [44]
где Ω — угловая частота вращения планеты, g — ускорение свободного падения планеты на средней поверхности океана, a — радиус планеты, U — внешний гравитационный приливной потенциал .
Уильям Томсон (лорд Кельвин) переписал термины импульса Лапласа, используя ротор , чтобы найти уравнение для завихренности . При определенных условиях это можно далее переписать как сохранение завихренности.
Анализ и прогноз приливов
Гармонический анализ
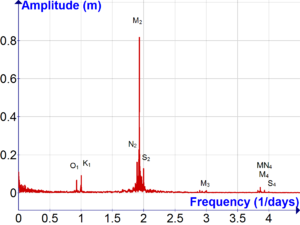
Улучшения Лапласа в теории были существенными, но они все еще оставляли предсказания в приблизительном состоянии. Это положение изменилось в 1860-х годах, когда локальные обстоятельства приливных явлений были более полно учтены Уильямом Томсоном , применившим анализ Фурье к приливным движениям как гармонический анализ . Работа Томсона в этой области была далее развита и расширена Джорджем Дарвином , применившим лунную теорию, современную ему.Символы Дарвина для приливных гармонических составляющих используются до сих пор, например:М: лунный/лунный;С: солнечный/солнечный;К: лунно-солнечный/луно-солнечный.
Гармонические разработки Дарвина приливообразующих сил были позднее улучшены, когда А. Т. Дудсон , применив лунную теорию Э. В. Брауна , [45] разработал приливообразующий потенциал (ППП) в гармонической форме, различая 388 приливных частот. [46] Работа Дудсона была выполнена и опубликована в 1921 году. [47] Дудсон разработал практическую систему для указания различных гармонических компонентов приливообразующего потенциала, чисел Дудсона , которая используется до сих пор.
С середины двадцатого века дальнейший анализ породил гораздо больше терминов, чем 388 Дудсона. Около 62 составляющих имеют достаточный размер для возможного использования в прогнозировании морских приливов, но иногда гораздо меньшее количество может предсказывать приливы с полезной точностью. Расчеты прогнозов приливов с использованием гармонических составляющих трудоемки, и с 1870-х до примерно 1960-х годов они выполнялись с использованием механической машины для прогнозирования приливов , специальной формы аналогового компьютера . В последнее время цифровые компьютеры, использующие метод обращения матрицы, используются для определения приливных гармонических составляющих непосредственно из записей мареографа.
Приливные составляющие
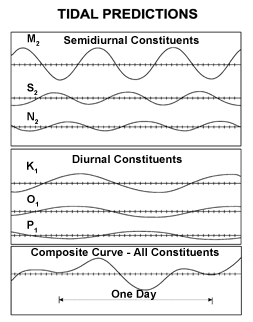
Приливные составляющие объединяются, чтобы дать бесконечно изменяющуюся совокупность из-за их различных и несоизмеримых частот: эффект визуализирован в анимации Американского математического общества, иллюстрирующей способ, которым компоненты раньше механически объединялись в машине для прогнозирования приливов. Амплитуды (половина амплитуды от пика до пика ) приливных составляющих приведены ниже для шести примеров местоположений: Истпорт, Мэн (ME), [48] Билокси, Миссисипи (MS), Сан-Хуан, Пуэрто-Рико (PR), Кадьяк, Аляска (AK), Сан-Франциско, Калифорния (CA) и Хило, Гавайи (HI).
полусуточный
| Разновидность | символ Дарвина | Период (ч) | Скорость (°/ч) | Коэффициенты Дудсона | Число Дудсона | Амплитуда в месте расположения примера (см) | заказ NOAA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| н 1 ( Л ) | н 2 ( м ) | н 3 ( у ) | н 4 ( мп ) | МНЕ | РС | PR | АК | КА | ПРИВЕТ | ||||||
| Главный лунный полусуточный | М 2 | 12.4206012 | 28.9841042 | 2 | 255.555 | 268.7 | 3.9 | 15.9 | 97.3 | 58.0 | 23.0 | 1 | |||
| Главный солнечный полусуточный | С 2 | 12 | 30 | 2 | 2 | −2 | 273.555 | 42.0 | 3.3 | 2.1 | 32,5 | 13.7 | 9.2 | 2 | |
| Более крупный лунный эллиптический полусуточный | Н 2 | 12.65834751 | 28.4397295 | 2 | −1 | 1 | 245.655 | 54.3 | 1.1 | 3.7 | 20.1 | 12.3 | 4.4 | 3 | |
| Большая лунная эекция | ν 2 | 12.62600509 | 28.5125831 | 2 | −1 | 2 | −1 | 247.455 | 12.6 | 0.2 | 0,8 | 3.9 | 2.6 | 0.9 | 11 |
| Вариационный | μ 2 | 12.8717576 | 27.9682084 | 2 | −2 | 2 | 237.555 | 2.0 | 0.1 | 0,5 | 2.2 | 0,7 | 0,8 | 13 | |
| Лунный эллиптический полусуточный второго порядка | 2 Н 2 | 12.90537297 | 27.8953548 | 2 | −2 | 2 | 235.755 | 6.5 | 0.1 | 0,5 | 2.4 | 1.4 | 0,6 | 14 | |
| Меньшая лунная эмиссия | λ2 | 12.22177348 | 29.4556253 | 2 | 1 | −2 | 1 | 263.655 | 5.3 | 0.1 | 0,7 | 0,6 | 0.2 | 16 | |
| Более крупный солнечный эллиптический | Т 2 | 12.01644934 | 29.9589333 | 2 | 2 | −3 | 272.555 | 3.7 | 0.2 | 0.1 | 1.9 | 0.9 | 0,6 | 27 | |
| Меньший солнечный эллиптический | Р 2 | 11.98359564 | 30.0410667 | 2 | 2 | −1 | 274.555 | 0.9 | 0.2 | 0.1 | 0.1 | 28 | |||
| Мелководье полусуточное | 2 СМ 2 | 11.60695157 | 31.0158958 | 2 | 4 | −4 | 291.555 | 0,5 | 31 | ||||||
| Меньший лунный эллиптический полусуточный | Л 2 | 12.19162085 | 29.5284789 | 2 | 1 | −1 | 265.455 | 13.5 | 0.1 | 0,5 | 2.4 | 1.6 | 0,5 | 33 | |
| лунно-солнечный полусуточный | К 2 | 11.96723606 | 30.0821373 | 2 | 2 | 275.555 | 11.6 | 0.9 | 0,6 | 9.0 | 4.0 | 2.8 | 35 | ||
Дневной
| Разновидность | символ Дарвина | Период (ч) | Скорость (°/ч) | Коэффициенты Дудсона | Число Дудсона | Амплитуда в месте расположения примера (см) | заказ NOAA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| н 1 ( Л ) | н 2 ( м ) | н 3 ( у ) | н 4 ( мп ) | МНЕ | РС | PR | АК | КА | ПРИВЕТ | ||||||
| лунно-солнечный суточный | К 1 | 23.93447213 | 15.0410686 | 1 | 1 | 165.555 | 15.6 | 16.2 | 9.0 | 39,8 | 36.8 | 16.7 | 4 | ||
| Лунный суточный | О 1 | 25.81933871 | 13.9430356 | 1 | −1 | 145.555 | 11.9 | 16.9 | 7.7 | 25.9 | 23.0 | 9.2 | 6 | ||
| Лунный суточный | ОО 1 | 22.30608083 | 16.1391017 | 1 | 3 | 185.555 | 0,5 | 0,7 | 0,4 | 1.2 | 1.1 | 0,7 | 15 | ||
| солнечный суточный | С 1 | 24 | 15 | 1 | 1 | −1 | 164.555 | 1.0 | 0,5 | 1.2 | 0,7 | 0.3 | 17 | ||
| Меньший лунный эллиптический суточный | М 1 | 24.84120241 | 14.4920521 | 1 | 155.555 | 0,6 | 1.2 | 0,5 | 1.4 | 1.1 | 0,5 | 18 | |||
| Меньший лунный эллиптический суточный | Дж 1 | 23.09848146 | 15.5854433 | 1 | 2 | −1 | 175.455 | 0.9 | 1.3 | 0,6 | 2.3 | 1.9 | 1.1 | 19 | |
| Более крупный лунный экционный суточный | ρ | 26.72305326 | 13.4715145 | 1 | −2 | 2 | −1 | 137.455 | 0.3 | 0,6 | 0.3 | 0.9 | 0.9 | 0.3 | 25 |
| Больший лунный эллиптический суточный | Вопрос 1 | 26.868350 | 13.3986609 | 1 | −2 | 1 | 135.655 | 2.0 | 3.3 | 1.4 | 4.7 | 4.0 | 1.6 | 26 | |
| Более крупный эллиптический суточный | 2 Кв 1 | 28.00621204 | 12.8542862 | 1 | −3 | 2 | 125.755 | 0.3 | 0,4 | 0.2 | 0,7 | 0,4 | 0.2 | 29 | |
| солнечный суточный | П 1 | 24.06588766 | 14.9589314 | 1 | 1 | −2 | 163.555 | 5.2 | 5.4 | 2.9 | 12.6 | 11.6 | 5.1 | 30 | |
Длительный период
| Разновидность | символ Дарвина | Период (ч) (дней) | Скорость (°/ч) | Коэффициенты Дудсона | Число Дудсона | Амплитуда в месте расположения примера (см) | заказ NOAA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| н 1 ( Л ) | н 2 ( м ) | н 3 ( у ) | н 4 ( мп ) | МНЕ | РС | PR | АК | КА | ПРИВЕТ | ||||||
| Лунный месяц | М м | 661.3111655 27.554631896 | 0,5443747 | 0 | 1 | −1 | 65.455 | 0,7 | 1.9 | 20 | |||||
| Солнечный полугодовой | С сб | 4383.076325 182.628180208 | 0,0821373 | 0 | 2 | 57.555 | 1.6 | 2.1 | 1.5 | 3.9 | 21 | ||||
| Солнечная годовая | С а | 8766.15265 365.256360417 | 0,0410686 | 0 | 1 | 56.555 | 5.5 | 7.8 | 3.8 | 4.3 | 22 | ||||
| Лунно-солнечный синодический двухнедельный | МС ф | 354.3670666 14.765294442 | 1.0158958 | 0 | 2 | −2 | 73.555 | 1.5 | 23 | ||||||
| Лунно-солнечный раз в две недели | М ж | 327.8599387 13.660830779 | 1.0980331 | 0 | 2 | 75.555 | 1.4 | 2.0 | 0,7 | 24 | |||||
Короткий период
| Разновидность | символ Дарвина | Период (ч) | Скорость (°/ч) | Коэффициенты Дудсона | Число Дудсона | Амплитуда в месте расположения примера (см) | заказ NOAA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| н 1 ( Л ) | н 2 ( м ) | н 3 ( у ) | н 4 ( мп ) | МНЕ | РС | PR | АК | КА | ПРИВЕТ | ||||||
| Мелководные приливы основных лунных | М 4 | 6.210300601 | 57.9682084 | 4 | 455.555 | 6.0 | 0,6 | 0.9 | 2.3 | 5 | |||||
| Мелководные приливы основных лунных | М 6 | 4.140200401 | 86.9523127 | 6 | 655.555 | 5.1 | 0.1 | 1.0 | 7 | ||||||
| Мелководье в течение дня | МК 3 | 8.177140247 | 44.0251729 | 3 | 1 | 365.555 | 0,5 | 1.9 | 8 | ||||||
| Мелководные приливы основных солнечных | С 4 | 6 | 60 | 4 | 4 | −4 | 491.555 | 0.1 | 9 | ||||||
| Мелководье четверть дня | МН 4 | 6.269173724 | 57.4238337 | 4 | −1 | 1 | 445.655 | 2.3 | 0.3 | 0.9 | 10 | ||||
| Мелководные приливы основных солнечных | С 6 | 4 | 90 | 6 | 6 | −6 | * | 0.1 | 12 | ||||||
| Лунный третичный | М 3 | 8.280400802 | 43.4761563 | 3 | 355.555 | 0,5 | 32 | ||||||||
| Мелководье в течение дня | 2 МК 3 | 8.38630265 | 42.9271398 | 3 | −1 | 345.555 | 0,5 | 0,5 | 1.4 | 34 | |||||
| Мелководье восьмой день | М 8 | 3.105150301 | 115.9364166 | 8 | 855.555 | 0,5 | 0.1 | 36 | |||||||
| Мелководье четверть дня | МС 4 | 6.103339275 | 58.9841042 | 4 | 2 | −2 | 473.555 | 1.8 | 0,6 | 1.0 | 37 | ||||
Числа Дудсона
Для того чтобы указать различные гармонические компоненты потенциала приливообразования, Дудсон разработал практическую систему, которая используется до сих пор, включающую то, что называется числами Дудсона, основанными на шести аргументах Дудсона или переменных Дудсона. Количество различных компонентов приливной частоты велико, но каждый соответствует определенной линейной комбинации шести частот с использованием малых целых кратных, положительных или отрицательных. В принципе, эти основные угловые аргументы могут быть указаны многочисленными способами; выбор Дудсоном его шести «аргументов Дудсона» широко использовался в приливной работе. В терминах этих аргументов Дудсона каждая приливная частота затем может быть указана как сумма, составленная из малых целых кратных каждого из шести аргументов. Полученные шесть малых целочисленных множителей эффективно кодируют частоту соответствующего приливного аргумента, и это числа Дудсона: на практике все, кроме первого, обычно смещены вверх на +5, чтобы избежать отрицательных чисел в записи. (В случае, если смещенный множитель превышает 9, система принимает X за 10 и E за 11.) [49]
Аргументы Дудсона указаны следующим образом, в порядке убывания частоты: [49]
- среднее лунное время, гринвичский часовой угол среднего Луны плюс 12 часов.
- средняя долгота Луны.
- средняя долгота Солнца.
- — долгота среднего перигея Луны.
- представляет собой отрицательную долготу среднего восходящего узла Луны на эклиптике.
- или — долгота среднего перигея Солнца.
В этих выражениях символы , и относятся к альтернативному набору фундаментальных угловых аргументов (обычно предпочитаемых для использования в современной лунной теории), в которых :
- — средняя аномалия Луны (расстояние от ее перигея).
- — средняя аномалия Солнца (расстояние от его перигея).
- — средний аргумент широты Луны (расстояние от ее узла).
- — средняя элонгация Луны (расстояние от Солнца).
На основе их комбинаций можно определить несколько вспомогательных переменных.
В терминах этой системы каждая приливная составляющая частота может быть идентифицирована ее числами Дудсона. Самая сильная приливная составляющая «M 2 » имеет частоту 2 цикла за лунные сутки, ее числа Дудсона обычно записываются как 255,555, что означает, что ее частота состоит из удвоенного первого аргумента Дудсона и нулевого числа всех остальных. Вторая по силе приливная составляющая «S 2 » находится под влиянием солнца, и ее числа Дудсона составляют 273,555, что означает, что ее частота состоит из удвоенного первого аргумента Дудсона, +2 раза второго, -2 раза третьего и нулевого числа каждого из трех других. [50] Это агрегируется в угловой эквивалент среднего солнечного времени +12 часов. Эти две самые сильные частоты компонентов имеют простые аргументы, для которых система Дудсона может показаться излишне сложной, но каждая из сотен других частот компонентов может быть кратко указана аналогичным образом, показывая в совокупности полезность кодирования.
Смотрите также
Примечания
- ^ Во всех океанах вода остается все время одинаковой по количеству и никогда не увеличивается и не уменьшается; но как вода в котле, которая вследствие ее соединения с теплом расширяется, так и воды океана разбухают с увеличением луны. Воды, хотя на самом деле не больше и не меньше, расширяются или сжимаются по мере увеличения или уменьшения луны в светлые и темные половины недели. - Вишну-пурана, книга II, гл. IV
- ^ Теперь я сам видел у кельтов морские приливы, как они описаны. Сделав различные предположения о том, почему столь огромная масса воды отступает и наступает, я пришел к выводу, что Аполлоний распознал настоящую истину. Ибо в одном из своих писем к индейцам он говорит, что океан выталкивается подводными влияниями или духами из нескольких пропастей, которые земля дает как под собой, так и вокруг себя, чтобы выдвигаться наружу и снова отступать, когда влияние или дух, подобно дыханию наших тел, уступает и отступает. И эта теория подтверждается течением болезней в Гадейре, ибо во время прилива души умирающих не покидают тела, и это вряд ли могло бы произойти, говорит он, если бы влияние или дух, о котором я говорил, также не продвигались к земле. Они также рассказывают вам о некоторых явлениях океана в связи с фазами луны, в соответствии с тем, как она рождается, достигает полноты и убывает. Эти явления я проверил, ибо океан точно идет в ногу с размером луны, уменьшаясь и увеличиваясь вместе с ней. - Филострат , Жизнь Аполлония Тианского , V
- ^ "Orbis virtutistractiæ, quæ est in Luna, porrigitur utque ad Terras, & prolectat aquas sub Zonam Torridam,… Celeriter vero Luna verticem transvolante, cum aquæ tam celeriter sequi non possint, fluxus quidem fit Oceani sub Torrida in Occidentem,…" ("Сфера подъемной силы, который [центр] находится в Луне, простирается до земли и притягивает воды под жаркую зону… Однако луна быстро летит через зенит; поскольку воды не могут следовать так быстро, прилив океана под жаркой [зоной] действительно направлен на запад,…») [19]
Ссылки
- ^ "Луна". Australian Indigenous Astronomy . Получено 8 октября 2020 г.
- ^ "«Преодоление разрыва» посредством австралийской культурной астрономии». Археоастрономия и этноастрономия – наведение мостов между культурами : 282–290 . 2011.
- ^ abcdef Табаррони, Г. (1989). «Приливы и Ньютон». Memorie della Società Astronomia Italiana . 60 : 770–777 . Бибкод : 1989MmSAI..60..769T . Проверено 27 декабря 2020 г.
- ^ abcdef Marmer, HA (март 1922). «Проблемы прилива». The Scientific Monthly . 14 (3): 209–222 .
- ^ abc Pugh, David T. (28 декабря 1987 г.). Приливы, нагоны и средний уровень моря (PDF) . JOHN WILEY & SONS. стр. 2– 4. ISBN 047191505X. Получено 27 декабря 2020 г. .
- ^ ab «Понимание приливов — от древних верований до современных решений уравнений Лапласа» (PDF) . Том 33, № 2. Новости SIAM.
- ^ abcd Хит, Томас Литтл (1913). Аристарх Самосский, древний Коперник. Герштейн — Университет Торонто. Оксфорд: Clarendon Press. С. 306–307 .
- ^ Картрайт, Дэвид Эдгар (1999). Приливы: Научная история. Cambridge University Press. стр. 6. ISBN 9780521797467. Получено 28 декабря 2020 г. .
- ^ Сенека , Де Провидентия , раздел IV
- ^ ab Cartwright, David E. (2001). «О происхождении знаний о морских приливах от античности до тринадцатого века». Earth Sciences History . 20 (2): 105– 126. Bibcode : 2001ESHis..20..105C. doi : 10.17704/eshi.20.2.m23118527q395675. JSTOR 24138749. Получено 27 декабря 2020 г.
- ^ Лусио Руссо , Flussi e riflussi , Feltrinelli, Милан, 2003, ISBN 88-07-10349-4 .
- ^ Ван дер Варден, BL (1987). «Гелиоцентрическая система в греческой, персидской и индуистской астрономии». Анналы Нью-Йоркской академии наук . 500 (1): 525– 545. Bibcode : 1987NYASA.500..525V. doi : 10.1111/j.1749-6632.1987.tb37224.x. S2CID 222087224.
- ^ Bede (2004). Расчет времени . Перевод Фейт Уоллис. Liverpool University Press. С. 64–65 . ISBN 978-0-85323-693-1.
- ^ ХЬЮЗ, ПОЛ. "ИЗУЧЕНИЕ РАЗВИТИЯ ПРИМИТИВНЫХ И СОВРЕМЕННЫХ ТАБЛИЦ ПРИЛИВОВ" (PDF) . Кандидатская диссертация, Ливерпульский университет Джона Мурса . Получено 27 декабря 2020 г. .
- ^ «Проект Принстон Данте: Основной браузер стихотворений (2.0)». dante.princeton.edu .
- ^ abcd Марина Толмачева (2014). Глик, Томас Ф. (ред.). География, Хорография . Routledge. стр. 188. ISBN 978-1135459321.
- ^ Саймон Стевин - Морской институт Фландрии (pdf, на голландском языке)
- ^ Пальмерино, Восприятие Галилеевой науки о движении в Европе семнадцатого века, стр. 200, op books.google.nl
- ^ Иоганн Кеплер, Astronomia nova … (1609), с. 5 Introductio in hoc opus (Введение к данной работе). Со страницы 5:
- ^ Иоганн Кеплер, Astronomia nova ... (1609), с. 5 Введения в hoc opus
- ^ ab Попова, Мария (27 декабря 2019 г.). «Как Кеплер изобрел научную фантастику... одновременно революционизируя наше понимание Вселенной». Brain Pickings . Получено 27 декабря 2020 г.
- ^ Юджин, Хехт (2019). «Кеплер и истоки теории гравитации». American Journal of Physics . 87 (3): 176– 185. Bibcode : 2019AmJPh..87..176H. doi : 10.1119/1.5089751. S2CID 126889093.
- ^ ab Rice University : Galileo's Theory of the Tides, автор Rossella Gigli, получено 10 марта 2010 г.
- ↑ Тайсон, Питер (29 октября 2002 г.). «Большая ошибка Галилея». NOVA . PBS . Получено 19 февраля 2014 г. .
- ^ Palmieri, Paolo (1998). Переосмысление теории приливов Галилея . Springer-Verlag. стр. 229.
- ^ Палмери, Паоло (1998). Переосмысление теории приливов Галилея . Springer-Verlag. стр. 227.
- ^ Нейлор, Рон (2007). «Приливная теория Галилея». Isis . 98 (1): 1– 22. Bibcode : 2007Isis...98....1N. doi : 10.1086/512829. PMID 17539198. S2CID 46174715.
- ^ Aiton, EJ (1955). «Теория приливов Декарта». Annals of Science . 11 (4): 337– 348. doi :10.1080/00033795500200335.
- ^ "Voltaire, Letter XIV". Архивировано из оригинала 13 апреля 2021 г. Получено 28 декабря 2020 г.
- ^ Картрайт, Дэвид Эдгар (1999). Приливы: Научная история. Cambridge University Press. стр. 31. ISBN 9780521797467. Получено 28 декабря 2020 г. .
- ^ "Статические приливы – теория равновесия". Архивировано из оригинала 10 апреля 2014 года . Получено 14 апреля 2014 года .
- ^ "Краткие заметки о динамической теории Лапласа". 20 ноября 2011 г. Архивировано из оригинала 2 апреля 2015 г. Получено 31 марта 2015 г.
- ^ "Динамика приливов" (PDF) . Faculty.washington.edu .
- ^ Ан, Кён-Джин (сентябрь 2009 г.). «Взгляд астронома на современные описания приливов в учебниках колледжей» (PDF) . Корейское общество наук о Земле . 30 (5): 671– 681. doi :10.5467/JKESS.2009.30.5.671.
- ^ Bryden, IG (2003). "Tidal Power Systems", в Meyers, RA (ред.) Encyclopedia of Physical Science and Technology . Aberdeen: Academic Press, стр. 753. doi:10.1016/b0-12-227410-5/00778-x
- ^ Флор Энтони. "Tides". Seafriends.org.nz . Получено 2 июня 2012 г.
- ^ «Причина и природа приливов».
- ^ "Scientific Visualization Studio TOPEX/Poseidon images". Svs.gsfc.nasa.gov . Получено 2 июня 2012 г. .
- ^ "TOPEX/Poseidon Западное полушарие: Модель высоты прилива : NASA/Goddard Space Flight Center Scientific Visualization Studio : Бесплатная загрузка и потоковая передача : Интернет-архив". 15 июня 2000 г.
- ^ "Данные TOPEX, используемые для моделирования фактических приливов за 15 дней с 2000 года". 15 июня 2000 г. Архивировано из оригинала 18 сентября 2015 г. Получено 14 сентября 2015 г.
- ^ http://www.geomag.us/info/Ocean/m2_CHAMP+longwave_SSH.swf
- ^ "OSU Tidal Data Inversion". Volkov.oce.orst.edu. Архивировано из оригинала 22 октября 2012 года . Получено 2 июня 2012 года .
- ^ "Анализ динамических и остаточных океанских приливов для улучшенного устранения наложений GRACE (DAROTA)". Архивировано из оригинала 2 апреля 2015 г.
- ^ «Уравнения приливов Лапласа и атмосферные приливы» (PDF) .
- ^ Картрайт, Дэвид Эдгар (1999). Приливы: Научная история. Cambridge University Press. С. 163–164 . ISBN 9780521797467.
- ^ S Casotto, F Biscani, «Полностью аналитический подход к гармоническому развитию потенциала приливообразования с учетом прецессии, нутации и возмущений, вызванных фигурными и планетарными членами», AAS Division on Dynamical Astronomy, апрель 2004 г., т. 36(2), 67.
- ^ AT Doodson (1921), «Гармоническое развитие потенциала приливов», Труды Лондонского королевского общества. Серия A, том 100, № 704 (1 декабря 1921 г.), стр. 305–329.
- ^ NOAA. "Eastport, ME Tidal Constituents". NOAA . Получено 22 мая 2012 г.
- ^ ab Melchior, P. (1971). «Прецессионно-нутационные колебания и приливной потенциал». Celestial Mechanics . 4 (2): 190– 212. Bibcode :1971CeMec...4..190M. doi :10.1007/BF01228823. S2CID 126219362.и уже цитируемый TD Moyer (2003).
- ^ См., например, уже цитированную работу Мельхиора (1971) на стр. 191.
Внешние ссылки
- Вклад спутниковой лазерной локации в изучение земных приливов Архивировано 28 июля 2013 г. на Wayback Machine
- Динамическая теория приливов
- Наблюдения за приливами
- Публикации Центра оперативных океанографических продуктов и услуг NOAA
- Понимание приливов и отливов
- 150 лет приливов на западном побережье
- Наши неумолимые приливы
- Система анализа приливов GeoTide
![{\displaystyle {\begin{aligned}{\frac {\partial \zeta }{\partial t}}&+{\frac {1}{a\cos(\varphi )}}\left[{\frac {\partial }{\partial \lambda }}(uD)+{\frac {\partial }{\partial \varphi }}\left(vD\cos(\varphi )\right)\right]=0,\\[2ex]{\frac {\partial u}{\partial t}}&-v\,2\Omega \sin(\varphi )+{\frac {1}{a\cos(\varphi )}}{\frac {\partial }{\partial \lambda }}\left(g\zeta +U\right)=0,\quad {\text{и}}\\[2ex]{\frac {\partial v}{\partial t}}&+u\,2\Omega \sin(\varphi )+{\frac {1}{a}}{\frac {\partial }{\partial \varphi }}\left(g\zeta +U\right)=0,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93fa08ee6fd9993a354e58f22257c7847c90666d)











