Трехзеркальный анастигмат
Конструкция рефлекторного телескопа
Трехзеркальный анастигмат формы Пола или Пола–Бейкера. Конструкция Пола имеет параболическое первичное зеркало со сферическими вторичным и третичным зеркалами; конструкция Пола–Бейкера немного изменяет вторичное зеркало, чтобы сделать фокальную плоскость плоской.

Трехзеркальный анастигмат — это телескоп- анастигмат , построенный с тремя изогнутыми зеркалами, что позволяет ему минимизировать все три основные оптические аберрации — сферическую аберрацию , кому и астигматизм . Это в основном используется для обеспечения широких полей зрения, намного больших, чем это возможно с телескопами всего с одной или двумя изогнутыми поверхностями.

Телескоп только с одним изогнутым зеркалом, например, телескоп Ньютона , всегда будет иметь аберрации. Если зеркало сферическое, оно будет страдать от сферической аберрации. Если зеркало сделано параболическим, чтобы исправить сферическую аберрацию, то оно обязательно должно страдать от комы и внеосевого астигматизма. С двумя изогнутыми зеркалами, например, телескопом Ричи-Кретьена , кома также может быть минимизирована. Это позволяет увеличить полезное поле зрения, а оставшийся астигматизм симметричен вокруг искаженных объектов, что позволяет проводить астрометрию по всему широкому полю зрения. Однако астигматизм можно уменьшить, включив третий изогнутый оптический элемент. Когда этот элемент является зеркалом, получается трехзеркальный анастигмат . На практике конструкция может также включать любое количество плоских складных зеркал , используемых для изгиба оптического пути в более удобные конфигурации.

История

Многие комбинации трех зеркальных фигур могут быть использованы для устранения всех аберраций третьего порядка. В общем случае они подразумевают решение относительно сложного набора уравнений. Однако некоторые конфигурации достаточно просты, чтобы их можно было разработать, исходя из нескольких интуитивных концепций.

Телескоп Пола

Первые были предложены в 1935 году Морисом Полем. [1] Основная идея решения Пола заключается в том, что сферические зеркала с апертурной диафрагмой в центре кривизны имеют только сферическую аберрацию — без комы или астигматизма (но они создают изображение на криволинейной поверхности с радиусом, равным половине радиуса кривизны сферического зеркала). Таким образом, если можно исправить сферическую аберрацию, можно получить очень широкое поле зрения. Это похоже на обычную конструкцию Шмидта , но Шмидт делает это с помощью рефракционной корректирующей пластины вместо третьего зеркала.

Идея Пола заключалась в том, чтобы начать с компрессора пучка Мерсенна, который выглядит как Кассегрен, сделанный из двух (конфокальных) параболоидов , с коллимированными входным и выходным пучками. Затем сжатый входной пучок направляется на сферическое третичное зеркало, что приводит к традиционной сферической аберрации. Ключевое понимание Пола заключается в том, что вторичное зеркало затем можно преобразовать обратно в сферическое зеркало.

Один из способов взглянуть на это — представить, что третичное зеркало, страдающее от сферической аберрации, заменено телескопом Шмидта с корректирующей пластиной в центре его кривизны. Если радиусы вторичного и третичного зеркал имеют одинаковую величину, но противоположный знак, и если центр кривизны третичного зеркала расположен непосредственно в вершине вторичного зеркала, то пластина Шмидта будет лежать поверх параболоидного вторичного зеркала. Таким образом, пластина Шмидта, необходимая для того, чтобы сделать третичное зеркало телескопом Шмидта, устраняется параболоидом, фигурирующим на выпуклом вторичном зеркале системы Мерсенна, поскольку каждый из них корректирует ту же величину сферической аберрации, но противоположный знак. Кроме того, поскольку система Мерсенна + Шмидта является суммой двух анастигматов (система Мерсенна является анастигматом, как и система Шмидта), результирующая система также является анастигматом, поскольку аберрации третьего порядка являются чисто аддитивными. [2] Кроме того, вторичный элемент теперь проще изготовить. Эта конструкция также называется Мерсенна–Шмидта , поскольку она использует конфигурацию Мерсенна в качестве корректора для телескопа Шмидта.

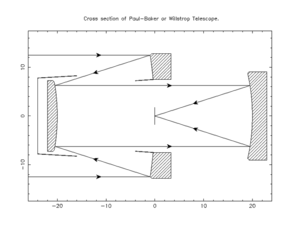
Телескоп Пола–Бейкера

Решение Пола имело изогнутую фокальную плоскость , но это было исправлено в конструкции Пола–Бейкера, представленной в 1969 году Джеймсом Гилбертом Бейкером . [3] Конструкция Пола–Бейкера добавляет дополнительное расстояние и изменяет форму вторичного зеркала на эллиптическую, что исправляет кривизну поля, делая фокальную плоскость плоской. [4]

телескоп Корша

Более общий набор решений был разработан Дитрихом Коршем в 1972 году. [5] Телескоп Корша исправлен на сферическую аберрацию , кому , астигматизм и кривизну поля и может иметь широкое поле зрения, гарантируя при этом малое количество рассеянного света в фокальной плоскости .

Телескоп Эйзенберга-Пирсона

Эйзенберг – Пирсон Двухзеркальный Трехповерхностный
Айзенберг твердый трехзеркальный анастигмат

Разновидностью конструкции Корша является телескоп с тремя поверхностями Two-Mirror [6], представленный Шаем Эйзенбергом и Эрлом Т. Пирсоном в 1987 году. Используя уравнения Корша с минимальными изменениями, количество зеркал сокращается с трех до двух путем объединения первичной поверхности и третичной поверхности на одном и том же зеркале. В одном варианте третичная поверхность идентична первичной, тогда как во втором варианте третичная поверхность показана отполированной в первичное зеркало. Телескопу Эйзенберга-Пирсона не требуется плоское складное зеркало для доступа к плоскости изображения, поскольку фокальная плоскость расположена за вторичным зеркалом. Компактная иллюстрация телескопа Корша, опубликованная в 1995 году Шаем Эйзенбергом [7], представляет собой сплошную версию конструкции с использованием полного внутреннего отражения (ПВО) для интеграции четвертого складного зеркала без виньетирования .


Примеры

  • Космический телескоп Джеймса Уэбба представляет собой трехзеркальный анастигмат, включающий эллипсоидальное первичное зеркало, гиперболоидальное вторичное зеркало и эллипсоидальное третье зеркало. [8]
  • В миссии «Евклид» используется телескоп Корша.
  • «Трехзеркальный телескоп Кембриджского университета» .Проект включает в себя 100-миллиметровую рабочую модель, построенную в 1985 году, и 500-миллиметровый прототип, построенный в 1986 году.
  • Телескоп обсерватории Веры К. Рубин (ранее известный как Большой синоптический обзорный телескоп) представляет собой конструкцию Эйзенберга-Пирсона с дополнительным рефракционным корректором.
  • Телескопы KH-11 Kennen (или, возможно, теперь отмененные Future Imagery Architecture ) могут быть трехзеркальными анастигматами, поскольку запасные телескопы, предоставленные НАСА Национальным разведывательным управлением, имеют именно такую ​​конструкцию.
  • Чрезвычайно большой телескоп будет иметь конструкцию с тремя зеркалами-анастигматами и двумя дополнительными плоскими складными зеркалами.
  • Спутники наблюдения Земли Deimos-2 и DubaiSat-2 оснащены трехзеркальным анастигматическим телескопом конструкции Корша. [9] [10]
  • Спектрометр Ralph imaging на космическом аппарате New Horizons
  • Космический телескоп Нэнси Грейс Роман , ранее называвшийся Широкоугольным инфракрасным обзорным телескопом (WFIRST), использует складной трехзеркальный анастигмат с эллипсоидальным первичным, гиперболоидальным вторичным и эллипсоидальным третичным зеркалами. [11] Более ранняя конструкция использовала внеосевой трехзеркальный анастигмат. [12]

Смотрите также

Ссылки

  1. ^ Пол, Морис (май 1935 г.). «Системы корректоров астрономических отражений». Revue d'Optique Théorique et Instrumentale . 14 (5): 169–202 .
  2. ^ Уилсон, Р. Н. (2007). Оптика телескопа-рефлектора I. Springer . стр. 227. ISBN 978-3-540-40106-3.
  3. ^ Бейкер, Дж. Г. (1969). «Об улучшении эффективности больших телескопов». Труды IEEE по аэрокосмическим и электронным системам . AES-5 (2): 261– 272. Bibcode : 1969ITAES...5..261B. doi : 10.1109/TAES.1969.309914. S2CID  51647158.
  4. ^ Сачек, В. (14 июля 2006 г.). «Пол-Бейкер и другие трехзеркальные анастигматические апланаты». Telescope-Optics.net . Получено 13 августа 2013 г. .
  5. ^ Корш, Дитрих (декабрь 1972 г.). «Замкнутое решение для трехзеркальных телескопов, исправленное на сферическую аберрацию, кому, астигматизм и кривизну поля». Прикладная оптика . 11 (12): 2986– 2987. Bibcode : 1972ApOpt..11.2986K. doi : 10.1364/AO.11.002986. PMID  20119447.
  6. ↑ Шай Эйзенберг и Эрл Т. Пирсон «Двухзеркальный трехповерхностный телескоп». Proc SPIE Vol. 751, стр. 24, январь 1987 г.
  7. ^ Йешаягу С. Айзенберг USP 5,930,055 «Линзовый аппарат»
  8. ^ Contreras, James W.; Lightsey, Paul A. (22 октября 2004 г.). "Оптическая конструкция и анализ космического телескопа Джеймса Уэбба: элемент оптического телескопа". В Sasian, Jose M.; Koshel, R. John; Manhart, Paul K.; Juergens, Richard C. (ред.). Novel Optical Systems Design and Optimization VII . Conference Proceedings of the SPIE. Vol. 5524. p. 30. Bibcode : 2004SPIE.5524...30C. doi : 10.1117/12.559871. S2CID  120352992.
  9. ^ «DEIMOS‑2: Экономически эффективная многоспектральная съемка с очень высоким разрешением» (PDF) .
  10. ^ «Технические характеристики DubaiSat 2».
  11. ^ Pasquale, Bert A.; et al. (17 сентября 2018 г.). «Оптическая конструкция и прогнозируемая производительность сборки оптики формирования изображений WFIRST phase-b и широкоугольного прибора». В Thibault, Simon; Mahajan, Virendra N.; Johnson, R. Barry (ред.). Current Developments in Lens Design and Optical Engineering XIX . Vol. 107450K. p. 18. Bibcode : 2018SPIE10745E..0KP. doi : 10.1117/12.2325859. hdl : 2060/20180006984 . ISBN 9781510620612. S2CID  126155297.
  12. ^ Content, DA; Goullioud, R.; Lehan, JP; Mentzell, JE (14 сентября 2011 г.). "Исследование торговли оптической конструкцией для широкоугольного инфракрасного обзорного телескопа [WFIRST]" (PDF) . В MacEwen, Howard A.; Breckinridge, James B. (ред.). Космические телескопы и инструменты УФ/оптического/ИК-диапазона: инновационные технологии и концепции V. Труды конференции SPIE. Том 8146. стр. 81460Y. Bibcode : 2011SPIE.8146E..0YC. doi : 10.1117/12.898528. hdl : 2060/20110023388 . S2CID  30254738.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Three-mirror_anastigmat&oldid=1230956955"