Лемма регулярности Семереди

В экстремальной теории графов лемма Семереди о регулярности утверждает, что граф можно разбить на ограниченное число частей так, чтобы ребра между частями были регулярными. Лемма показывает, что некоторые свойства случайных графов можно применять к плотным графам, например, подсчет копий заданного подграфа внутри графов. Эндре Семереди доказал лемму над двудольными графами для своей теоремы об арифметических прогрессиях в 1975 году и для общих графов в 1978 году. Варианты леммы используют различные понятия регулярности и применяются к другим математическим объектам, таким как гиперграфы .

Чтобы формально сформулировать лемму Семереди о регулярности, мы должны формализовать, что на самом деле означает распределение ребер между частями, ведущими себя «почти случайно». Под «почти случайно» мы подразумеваем понятие, называемое ε -регулярностью. Чтобы понять, что это значит, мы сначала дадим некоторые определения. В дальнейшем G — это граф с множеством вершин V .

Определение 1. Пусть X ,  Y — непересекающиеся подмножества V. Плотность ребер пары ( X ,  Y ) определяется как:

${\displaystyle d(X,Y):={\frac {\left|E(X,Y)\right|}{|X||Y|}}}$

где E ( X ,  Y ) обозначает множество ребер, имеющих одну конечную вершину в X и одну в Y .

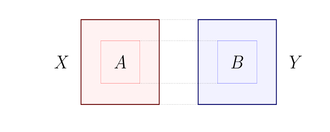
Мы называем пару частей ε -регулярной, если, когда вы берете большое подмножество каждой части, их плотность ребер не слишком сильно отличается от плотности ребер пары частей. Формально,

Определение 2. При ε > 0 пара множеств вершин X и Y называется ε -регулярной , если для всех подмножеств A  ⊆  X , B  ⊆  Y, удовлетворяющих | A | ≥ ε| X | , | B | ≥ ε| Y | , имеем

${\displaystyle \left|d(X,Y)-d(A,B)\right|\leq \varepsilon .}$

Естественным способом определения ε -регулярного разбиения должен быть тот, где каждая пара частей является ε -регулярной. Однако некоторые графы, такие как полуграфы , требуют, чтобы многие пары разбиений (но небольшая часть всех пар) были нерегулярными. ^[1] Поэтому мы определим ε -регулярные разбиения как те, где большинство пар частей являются ε -регулярными.

Определение 3. Разбиение на множества называется -регулярным разбиением, если${\displaystyle V}$${\displaystyle к}$${\displaystyle {\mathcal {P}}=\{V_{1},\ldots,V_{k}\}}$${\displaystyle \varepsilon}$

${\displaystyle \sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}|V_{i}||V_{j}|\leq \varepsilon |V(G)|^{2}}$

Теперь мы можем сформулировать лемму:

Лемма регулярности Семереди. Для любого ε > 0 и положительного целого числа m существует целое число M такое, что если G — граф с по крайней мере M вершинами, то существует целое число k в диапазоне m  ≤  k  ≤  M и ε -регулярное разбиение множества вершин графа G на k множеств.

Граница M для числа частей в разбиении графа, полученная в результате доказательств леммы Семереди о регулярности, очень велика и задается итерированной экспонентой уровня O(ε ⁻⁵ ) от m . Одно время надеялись, что истинная граница будет намного меньше, что имело бы несколько полезных приложений. Однако Гауэрс (1997) нашел примеры графов, для которых M действительно растет очень быстро и по крайней мере так же велика, как итерированная экспонента уровня ε ^−1/16 от m . ^[2]

Найдем ε-регулярное разбиение для заданного графа, следуя алгоритму:

1. Начните с раздела
2. Хотя разбиение не является ε-регулярным:
   • Найдите подмножества, которые свидетельствуют о ε-нерегулярности для каждой нерегулярной пары.
3. Уточните раздел, используя все подмножества свидетелей.

Мы применяем технику, называемую аргументом приращения энергии , чтобы показать, что этот процесс останавливается после ограниченного числа шагов. Для этого мы определяем меру, которая должна увеличиваться на определенную величину на каждом шаге, но она ограничена сверху и, таким образом, не может увеличиваться бесконечно. Эта мера называется «энергия», поскольку она является величиной .${\displaystyle L^{2}}$

Определение 4. Пусть U ,  W — подмножества V. Набор . Энергия пары ( U ,  W ) определяется как:${\displaystyle |V|=n}$

${\displaystyle q(U,W):={\frac {|U||W|}{n^{2}}}d(U,W)^{2}}$

Для разделов U и W мы определяем энергию как сумму энергий между каждой парой частей:${\displaystyle {\mathcal {P}}_{U}=\{U_{1},\ldots,U_{k}\}}$${\displaystyle {\mathcal {P}}_{W}=\{W_{1},\ldots,W_{l}\}}$

${\displaystyle q({\mathcal {P}}_{U},{\mathcal {P}}_{W}):=\sum _{i=1}^{k}\sum _{j=1}^{l}q(U_{i},W_{j})}$

Наконец , для разбиения V определим энергию как . В частности,${\displaystyle {\mathcal {P}}=\{V_{1},\ldots,V_{k}\}}$${\displaystyle {\mathcal {P}}}$${\displaystyle q({\mathcal {P}},{\mathcal {P}})}$

${\displaystyle q({\mathcal {P}})=\sum _{i=1}^{k} \sum _{j=1}^{k}q(V_{i},V_{j}) =\sum _{i=1}^{k}\sum _{j=1}^{k}{\frac {|V_{i}||V_{j}|}{n^{2}}}d(V_{i},V_{j})^{2}}$

Обратите внимание, что энергия находится в диапазоне от 0 до 1, поскольку плотность ребер ограничена сверху 1:

${\displaystyle q({\mathcal {P}})=\sum _{i=1}^{k}\sum _{j=1}^{k}{\frac {|V_{i}||V_ {j}|}{n^{2}}}d(V_{i},V_{j})^{2}\leq \sum _{i=1}^{k}\sum _{j=1}^{k}{\frac {|V_{i}||V_{j}|}{n^{2}}}=1}$

Теперь начнем с доказательства того, что энергия не уменьшается при уточнении.

Лемма 1. (Энергия не убывает при разбиении) Для любых разбиений и множеств вершин и , .${\displaystyle {\mathcal {P}}_{U}}$${\displaystyle {\mathcal {P}}_{W}}$${\displaystyle U}$${\displaystyle W}$${\displaystyle q({\mathcal {P}}_{U},{\mathcal {P}}_{W})\geq q(U,W)}$

Доказательство: Пусть и . Выберем вершины равномерно из и равномерно из , причем частично и частично . Затем определим случайную величину . Давайте рассмотрим свойства . Ожидание равно${\displaystyle {\mathcal {P}}_{U}=\{U_{1},\ldots ,U_{k}\}}$${\displaystyle {\mathcal {P}}_{W}=\{W_{1},\ldots ,W_{l}\}}$${\displaystyle x}$${\displaystyle U}$${\displaystyle y}$${\displaystyle W}$${\displaystyle x}$${\displaystyle U_{i}}$${\displaystyle y}$${\displaystyle W_{j}}$${\displaystyle Z=d(U_{i},W_{j})}$${\displaystyle Z}$

${\displaystyle \mathbb {E} [Z]=\sum _{i=1}^{k}\sum _{j=1}^{l}{\frac {|U_{i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})={\frac {e(U,W)}{|U||W|}}=d(U,W)}$

Второй момент -

${\displaystyle \mathbb {E} [Z^{2}]=\sum _{i=1}^{k}\sum _{j=1}^{l}{\frac {|U_{i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})^{2}={\frac {n^{2}}{|U||W|}}q({\mathcal {P}}_{U},{\mathcal {P}}_{W})}$

По выпуклости, . Переставляя, получаем, что для всех .${\displaystyle \mathbb {E} [Z^{2}]\geq \mathbb {E} [Z]^{2}}$${\displaystyle q({\mathcal {P}}_{U},{\mathcal {P}}_{W})\geq q(U,W)}$${\displaystyle U,W}$${\displaystyle \square }$

Если каждая часть далее разбивается, новое разбиение называется уточнением . Теперь, если , применение Леммы 1 к каждой паре доказывает, что для каждого уточнения , . Таким образом, шаг уточнения в алгоритме не теряет никакой энергии.${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {P}}=\{V_{1},\ldots ,V_{m}\}}$${\displaystyle (V_{i},V_{j})}$${\displaystyle {\mathcal {P'}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle q({\mathcal {P'}})\geq q({\mathcal {P}})}$

Лемма 2. (Лемма о повышении энергии) Если не является -регулярным, как следует из , то,${\displaystyle (U,W)}$${\displaystyle \varepsilon }$${\displaystyle U_{1}\subset U,W_{1}\subset W}$

${\displaystyle q\left(\{U_{1},U\backslash U_{1}\},\{W_{1},W\backslash W_{1}\}\right)>q(U,W)+\varepsilon ^{4}{\frac {|U||W|}{n^{2}}}}$

Доказательство: Определим , как указано выше. Тогда,${\displaystyle Z}$

${\displaystyle Var(Z)=\mathbb {E} [Z^{2}]-\mathbb {E} [Z]^{2}={\frac {n^{2}}{|U||W|}}\left(q\left(\{U_{1},U\backslash U_{1}\},\{W_{1},W\backslash W_{1}\}\right)-q(U,W)\right)}$

Но заметьте, что с вероятностью (соответствующей и ), поэтому${\displaystyle |Z-\mathbb {E} [Z]|=|d(U_{1},W_{1})-d(U,W)|}$${\displaystyle {\frac {|U_{1}|}{|U|}}{\frac {|W_{1}|}{|W|}}}$${\displaystyle x\in U_{1}}$${\displaystyle y\in W_{1}}$

${\displaystyle Var(Z)=\mathbb {E} [(Z-\mathbb {E} [Z])^{2}]\geq {\frac {|U_{1}|}{|U|}}{\frac {|W_{1}|}{|W|}}(d(U_{1},W_{1})-d(U,W))^{2}>\varepsilon \cdot \varepsilon \cdot \varepsilon ^{2}}$ ${\displaystyle \square }$

Теперь мы можем доказать аргумент о приращении энергии, который показывает, что энергия существенно увеличивается при каждой итерации алгоритма.

Лемма 3 (лемма об увеличении энергии) Если разбиение не является -регулярным, то существует уточнение , в котором каждое разбивается на не более чем части, такие, что${\displaystyle {\mathcal {P}}=\{V_{1},\ldots ,V_{k}\}}$${\displaystyle V(G)}$${\displaystyle \varepsilon }$${\displaystyle {\mathcal {Q}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle V_{i}}$${\displaystyle 2^{k}}$

${\displaystyle q({\mathcal {Q}})\geq q({\mathcal {P}})+\varepsilon ^{5}.}$

Доказательство: Для всех таких, что не является -регулярным, найдите и , которые являются свидетелями нерегулярности (сделайте это одновременно для всех нерегулярных пар). Пусть будет общим уточнением по 's. Каждый из них разбивается на не более чем части по желанию. Затем,${\displaystyle (i,j)}$${\displaystyle (V_{i},V_{j})}$${\displaystyle \varepsilon }$${\displaystyle A^{i,j}\subset V_{i}}$${\displaystyle A^{j,i}\subset V_{j}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle A^{i,j}}$${\displaystyle V_{i}}$${\displaystyle 2^{k}}$

${\displaystyle q({\mathcal {Q}})=\sum _{(i,j)\in [k]^{2}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})=\sum _{(V_{i},V_{j}){\text{ }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})+\sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})}$

Где разбиение задано . По лемме 1 указанная величина не менее${\displaystyle {\mathcal {Q}}_{V_{i}}}$${\displaystyle V_{i}}$${\displaystyle {\mathcal {Q}}}$

${\displaystyle \sum _{(V_{i},V_{j}){\text{ }}\varepsilon {\text{-regular}}}q(V_{i},V_{j})+\sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}q(\{A^{i,j},V_{i}\backslash A^{i,j}\},\{A^{j,i},V_{j}\backslash A^{j,i}\})}$

Так как при создании разрезается на , то и уточнение . По лемме 2 указанная выше сумма не менее${\displaystyle V_{i}}$${\displaystyle A^{i,j}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle {\mathcal {Q}}_{V_{i}}}$${\displaystyle \{A^{i,j},V_{i}\backslash A^{i,j}\}}$

${\displaystyle \sum _{(i,j)\in [k]^{2}}q(V_{i},V_{j})+\sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}\varepsilon ^{4}{\frac {|V_{i}||V_{j}|}{n^{2}}}}$

Но вторая сумма по крайней мере не меньше, так как не является -регулярной, поэтому выводим искомое неравенство.${\displaystyle \varepsilon ^{5}}$${\displaystyle {\mathcal {P}}}$${\displaystyle \varepsilon }$${\displaystyle \square }$

Теперь, начиная с любого разбиения, мы можем продолжать применять Лемму 3 до тех пор, пока полученное разбиение не будет -регулярным. Но на каждом шаге энергия увеличивается на , и она ограничена сверху 1. Затем этот процесс может повторяться максимальное количество раз, прежде чем он прекратится, и мы должны иметь -регулярное разбиение.${\displaystyle \varepsilon }$${\displaystyle \varepsilon ^{5}}$${\displaystyle \varepsilon ^{-5}}$${\displaystyle \varepsilon }$

Если у нас достаточно информации о регулярности графа, мы можем подсчитать количество копий определенного подграфа внутри графа с небольшой погрешностью.

Лемма о подсчете графов. Пусть будет графом с , и пусть . Пусть будет -вершинным графом с множествами вершин, таким что является -регулярным всякий раз, когда . Тогда число помеченных копий в находится в пределах${\displaystyle H}$${\displaystyle V(H)=[k]}$${\displaystyle \varepsilon >0}$${\displaystyle G}$${\displaystyle n}$${\displaystyle V_{1},\dots ,V_{k}\subseteq V(G)}$${\displaystyle (V_{i},V_{j})}$${\displaystyle \varepsilon }$${\displaystyle \{i,j\}\in E(H)}$${\displaystyle H}$${\displaystyle G}$${\displaystyle e(H)\varepsilon |V_{1}|\cdots |V_{k}|}$

${\displaystyle \left(\prod _{\{i,j\}\in E(H)}d(V_{i},V_{j})\right)\left(\prod _{i=1}^{k}|V_{i}|\right).}$

Это можно объединить с леммой Семереди о регулярности, чтобы доказать лемму об удалении графа . Лемма об удалении графа может быть использована для доказательства теоремы Рота об арифметических прогрессиях , ^[3] а ее обобщение, лемма об удалении гиперграфа , может быть использовано для доказательства теоремы Семереди . ^[4]

Лемма об удалении графа обобщается на индуцированные подграфы , рассматривая редактирование ребер вместо удаления только ребер. Это было доказано Алоном, Фишером, Кривелевичем и Сегеди в 2000 году. ^[5] Однако для этого потребовалась более сильная вариация леммы о регулярности.

Лемма регулярности Семереди не дает значимых результатов в разреженных графах . Поскольку разреженные графы имеют субконстантную плотность ребер, -регулярность тривиально выполняется. Хотя результат кажется чисто теоретическим, были предприняты некоторые попытки ^{[6] [7]} использовать метод регулярности в качестве техники сжатия для больших графов.${\displaystyle \varepsilon }$

Другое понятие регулярности было введено Фризом и Каннаном, известное как лемма о слабой регулярности. ^[8] Эта лемма определяет более слабое понятие регулярности, чем у Семереди, которое использует лучшие границы и может использоваться в эффективных алгоритмах.

Для данного графа разбиение его вершин называется регулярным по Фризу-Каннану, если для любой пары множеств :${\displaystyle G=(V,E)}$${\displaystyle {\mathcal {P}}=\{V_{1},\ldots ,V_{k}\}}$ ${\displaystyle \epsilon }$${\displaystyle S,T\subseteq V}$

${\displaystyle \left|e(S,T)-\sum _{i,j=1}^{k}d(V_{i},V_{j})|S\cap V_{i}||T\cap V_{j}|\right|\leq \epsilon |V|^{2}}$

Лемма о слабой регулярности для графов утверждает, что каждый граф имеет слабо -регулярное разбиение не более чем на части.${\displaystyle \epsilon }$${\displaystyle 4^{\epsilon ^{-2}}}$

Это понятие можно распространить на графоны , определив оператор шага. Учитывая графон и разбиение , мы можем определить как шаг-графон с шагами, заданными как и значениями, заданными усреднением по каждому шагу.${\displaystyle W}$${\displaystyle {\mathcal {P}}}$${\displaystyle [0,1]}$${\displaystyle W_{\mathcal {P}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle W}$

Разбиение является слабо -регулярным, если:${\displaystyle {\mathcal {P}}}$${\displaystyle \epsilon }$

${\displaystyle \|W-W_{\mathcal {P}}\|_{\square }\leq \epsilon }$

Лемма о слабой регулярности для графонов утверждает, что каждый графон имеет слабое -регулярное разбиение на не более чем части. Как и в случае с леммой о регулярности Семереди, слабая регулярность также индуцирует лемму о подсчете.${\displaystyle \epsilon }$${\displaystyle 4^{\epsilon ^{-2}}}$

Одной из первоначальных мотиваций для разработки леммы о слабой регулярности был поиск эффективного алгоритма для оценки максимального разреза в плотном графе . ^[8] Было показано, что аппроксимация задачи максимального разреза за пределами 16/17 является NP-трудной , ^[9] однако алгоритмическая версия леммы о слабой регулярности дает эффективный алгоритм для аппроксимации максимального разреза для плотных графов в пределах аддитивной ошибки. ^[8] Эти идеи были далее развиты в эффективные алгоритмы выборки для оценки максимального разреза в плотных графах. ^[10]${\displaystyle \epsilon n^{2}}$

Меньшие границы леммы о слабой регулярности допускают эффективные алгоритмы для нахождения -регулярного разбиения. ^[11] Регулярность графа далее использовалась в различных областях теоретической информатики , таких как умножение матриц ^[12] и сложность связи . ^[13]${\displaystyle \epsilon }$

Сильная лемма о регулярности является более сильной вариацией леммы о регулярности, доказанной Алоном , Фишером, Кривелевичем и Сегеди в 2000 году. ^[5] Интуитивно она предоставляет информацию о нерегулярных парах и может быть применена для доказательства леммы об удалении индуцированного графа .

Для любой бесконечной последовательности констант существует целое число такое, что для любого графа можно получить два (справедливых) разбиения , и такое, что выполняются следующие свойства:${\displaystyle \epsilon _{0}\geq \epsilon _{1}\geq ...>0}$${\displaystyle M}$${\displaystyle G}$${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {Q}}}$

• ${\displaystyle {\mathcal {Q}}}$уточняет , то есть каждая часть представляет собой объединение некоторого набора частей в .${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {Q}}}$
• ${\displaystyle {\mathcal {P}}}$является -регулярным и является -регулярным.${\displaystyle \epsilon _{0}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle \epsilon _{|{\mathcal {P}}|}}$
• ${\displaystyle q({\mathcal {Q}})<q({\mathcal {P}})+\epsilon _{0}}$
• ${\displaystyle |{\mathcal {Q}}|\leq M}$

Мы применяем лемму регулярности повторно, чтобы доказать более сильную версию. Грубый план:

• Начните с обычного раздела${\displaystyle {\mathcal {P}}_{0}}$${\displaystyle \epsilon _{0}}$

• Повторно находим его уточнение, которое является регулярным. Если приращение энергии , мы просто возвращаем . В противном случае заменяем на и продолжаем.${\displaystyle {\mathcal {Q}}}$${\displaystyle \epsilon _{|{\mathcal {P}}|}}$${\displaystyle {\mathcal {Q}}\leq \epsilon _{0}}$${\displaystyle ({\mathcal {P}},{\mathcal {Q}})}$${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {Q}}}$

Начнем с регулярного разбиения с частями. Здесь соответствует границе частей в лемме о регулярности, когда . ${\displaystyle {\mathcal {P}}_{0}}$${\displaystyle \epsilon _{0}}$${\displaystyle G}$${\displaystyle \leq M(\epsilon _{0})}$${\displaystyle M(t)}$${\displaystyle \epsilon =t}$

Теперь для , мы устанавливаем , чтобы быть регулярным уточнением с частями. По аргументу приращения энергии, . Поскольку энергия ограничена в , должно быть некоторое такое, что . Мы возвращаем как . ${\displaystyle i=0,1,\cdots }$${\displaystyle {\mathcal {P_{i+1}}}}$${\displaystyle \epsilon _{|P_{i}|}}$${\displaystyle {\mathcal {P_{i}}}}$${\displaystyle \leq M(\epsilon _{|P_{i}|})|{\mathcal {P}}_{i}|}$${\displaystyle q({\mathcal {P}}_{i+1})\geq q({\mathcal {P}}_{i})}$${\displaystyle [0,1]}$${\displaystyle i\leq 1/\epsilon _{0}+1}$${\displaystyle q({\mathcal {P}}_{i+1})-q({\mathcal {P}}_{i})<\epsilon _{0}}$${\displaystyle ({\mathcal {P}}_{i},{\mathcal {P}}_{i+1})}$${\displaystyle ({\mathcal {P}},{\mathcal {Q}})}$

По нашему выбору регулярных и уточняющих условий выполняется. Условие энергии выполняется тривиально. Теперь мы рассуждаем о числе частей. Мы используем индукцию, чтобы показать, что , существует такое, что . Задавая , мы имеем . Обратите внимание, что когда , , поэтому мы могли бы задать и утверждение верно для . Задавая , мы имеем${\displaystyle {\mathcal {P}}_{i+1},}$${\displaystyle \forall i}$${\displaystyle M_{i}}$${\displaystyle |{\mathcal {P}}_{i}|\leq M_{i}}$${\displaystyle M_{0}=M(\epsilon _{0})}$${\displaystyle |{\mathcal {P}}_{0}|\leq M_{0}}$${\displaystyle |P_{i}|\leq M_{i}}$${\displaystyle |P_{i+1}|\leq M(\epsilon _{|P_{i}|})|{\mathcal {P}}_{i}|\leq M(\epsilon _{|M_{i}|})M_{i}}$${\displaystyle M_{i+1}=M(\epsilon _{|M_{i}|})M_{i}}$${\displaystyle i+1}$${\displaystyle M=\max _{i\leq 1/\epsilon _{0}+2}M_{i}}$${\displaystyle |P|,|Q|\leq M.}$

Разбиение является справедливым, если размеры любых двух множеств отличаются не более чем на . Уравнивая в каждом раунде итерации, доказательство леммы о регулярности можно было бы использовать для доказательства справедливой версии леммы о регулярности. А заменив лемму о регулярности ее справедливой версией, доказательство выше могло бы доказать справедливую версию сильной леммы о регулярности, где и являются справедливыми разбиениями. ${\displaystyle 1}$${\displaystyle {\mathcal {P}}}$${\displaystyle {\mathcal {Q}}}$

Для любой бесконечной последовательности констант существует такая, что существуют разбиение и подмножества для каждой из них , где выполняются следующие свойства:${\displaystyle \epsilon _{0}\geq \epsilon _{1}\geq ...>0}$${\displaystyle \delta >0}$${\displaystyle {\mathcal {P}}={V_{1},...,V_{k}}}$${\displaystyle W_{i}\subset V_{i}}$${\displaystyle i}$

• ${\displaystyle |W_{i}|>\delta n}$
• ${\displaystyle (W_{i},W_{j})}$является -регулярным для каждой пары${\displaystyle \epsilon _{|{\mathcal {P}}|}}$${\displaystyle 1\leq i\leq j\leq k}$
• ${\displaystyle |d(W_{i},W_{j})-d(V_{i},V_{j})|\leq \epsilon _{0}}$для всех, кроме пар${\displaystyle \epsilon _{0}|{\mathcal {P}}|^{2}}$${\displaystyle 1\leq i\leq j\leq k}$

Следствие глубже исследует малое приращение энергии. Оно дает нам раздел вместе с подмножествами с большими размерами из каждой части, которые попарно регулярны. Кроме того, плотность между соответствующими парами подмножеств отличается "не сильно" от плотности между соответствующими частями.

Мы докажем только более слабый результат, где второе условие требует только быть -регулярным для . Полную версию можно доказать, выбрав больше подмножеств из каждой части, которые в основном попарно регулярны, и объединив их вместе. ${\displaystyle (W_{i},W_{j})}$${\displaystyle \epsilon _{|{\mathcal {P}}|}}$${\displaystyle 1\leq i<j\leq k}$

Пусть . Применим лемму о сильной регулярности, чтобы найти справедливое , которое является регулярным разбиением , и справедливое , которое является регулярным измельчением , такое, что и . ${\displaystyle r=\epsilon _{0}^{3}/20}$${\displaystyle {\mathcal {P}}}$${\displaystyle r}$${\displaystyle {\mathcal {Q}}}$${\displaystyle r/|P|^{4}}$${\displaystyle {\mathcal {P}}}$${\displaystyle q({\mathcal {Q}})-q({\mathcal {P}})\leq r}$${\displaystyle |{\mathcal {Q}}|\leq M}$

Теперь предположим , что мы случайным образом выбираем вершину из каждого и пусть будет набором, содержащим в . Мы утверждаем, что подмножества удовлетворяют всем условиям с вероятностью . ${\displaystyle P=\{V_{1},\cdots ,V_{k}\}}$${\displaystyle v_{i}}$${\displaystyle V_{i}}$${\displaystyle W_{i}}$${\displaystyle v_{i}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle W_{i}}$${\displaystyle >0}$

Задавая первое условие, тривиально верно, поскольку является справедливым разделением. Поскольку не более пар вершин находятся между нерегулярными парами в , вероятность того, что пара и является нерегулярной , по объединению границ, вероятность того, что по крайней мере одна пара , является нерегулярной . Обратите внимание, что ${\displaystyle \delta ={\frac {1}{2M}}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle {\frac {r}{|P|^{4}}}{\binom {n}{2}}\leq \epsilon _{0}{\frac {|V_{i}||V_{j}|}{3|P|^{2}}}}$${\displaystyle {\mathcal {Q}}}$${\displaystyle W_{i}}$${\displaystyle W_{j}}$${\displaystyle \leq {\frac {1}{3|P|^{2}}}}$${\displaystyle W_{i}}$${\displaystyle W_{i}}$${\displaystyle \leq 1/3}$

${\displaystyle {\begin{aligned}r&\geq q({\mathcal {Q}})-q({\mathcal {P}})\\&=\sum _{i,j}{\frac {|V_{i}||V_{j}|}{n^{2}}}\mathbb {E} |d(W_{i},W_{j})-d(V_{i},V_{j})|^{2}\\&\geq \sum _{i,j}{\frac {1}{4|P|^{2}}}\mathbb {E} |d(W_{i},W_{j})-d(V_{i},V_{j})|^{2}\\&={\frac {1}{4|P|^{2}}}\mathbb {E} \sum _{i,j}|d(W_{i},W_{j})-d(V_{i},V_{j})|^{2}\end{aligned}}}$

Итак, по неравенству Маркова , с вероятностью максимум пары могли бы иметь . По объединению границ вероятность того, что все условия выполняются . ${\displaystyle P(\sum _{i,j}|d(W_{i},W_{j})-d(V_{i},V_{j})|^{2}\geq 8|P|^{2}r)\leq 1/2}$${\displaystyle \geq 1/2}$${\displaystyle \epsilon _{0}|P|^{2}}$${\displaystyle d(W_{i},W_{j})-d(V_{i},V_{j})\geq \epsilon _{0}}$${\displaystyle \geq 1-1/2-1/3>0}$

Семереди (1975) впервые ввел более слабую версию этой леммы, ограниченную двудольными графами, чтобы доказать теорему Семереди , ^[14] а в (Семереди 1978) он доказал полную лемму. ^[15] Расширения метода регулярности на гиперграфы были получены Редлем и его коллегами ^{[16] [17] [18]} и Гауэрсом . ^{[19] [20]}

Янош Комлош , Габор Шаркёзи и Эндре Семереди позже (в 1997 году) доказали в лемме о раздутии ^{[21] [22]} , что регулярные пары в лемме о регулярности Семереди ведут себя как полные двудольные графы при правильных условиях. Лемма позволила глубже изучить природу вложений больших разреженных графов в плотные графы.

Первая конструктивная версия была предоставлена ​​Алоном, Дьюком, Лефманном, Рёдлем и Юстером. ^[23] Впоследствии Фриз и Каннан предложили другую версию и расширили ее до гиперграфов. ^[24] Позже они создали другую конструкцию благодаря Алану Фризу и Рави Каннану, которая использует сингулярные значения матриц. ^[25] Можно найти более эффективные недетерминированные алгоритмы, как формально описано в блоге Теренса Тао ^[26] и неявно упомянуто в различных статьях. ^{[27] [28] [29]}

Неравенство Теренса Тао расширяет лемму регулярности Семереди, пересматривая ее с точки зрения теории вероятностей и теории информации вместо теории графов. ^[30] Теренс Тао также предоставил доказательство леммы, основанное на спектральной теории, используя матрицы смежности графов. ^[31]

Невозможно доказать вариант леммы о регулярности, в котором все пары множеств разбиений являются регулярными. Некоторые графы, такие как полуграфы , требуют, чтобы многие пары разбиений (но небольшая часть всех пар) были нерегулярными. ^[1]

Распространенным вариантом определения -регулярного разбиения является требование, чтобы все наборы вершин имели одинаковый размер, при этом оставшиеся вершины собираются в "ошибочном"-наборе, размер которого составляет не более -доли размера набора вершин .${\displaystyle \varepsilon }$${\displaystyle V_{0}}$${\displaystyle \varepsilon }$${\displaystyle G}$

Более сильная вариация леммы регулярности была доказана Алоном, Фишером, Кривелевичем и Сегеди при доказательстве леммы об удалении индуцированного графа. Это работает с последовательностью вместо одного и показывает, что существует разбиение с чрезвычайно регулярным уточнением, где уточнение не имеет слишком большого приращения энергии.${\displaystyle \varepsilon }$

Лемму регулярности Семереди можно интерпретировать как утверждение, что пространство всех графов полностью ограничено (и, следовательно, предкомпактно ) в подходящей метрике ( расстоянии разреза ). Пределы в этой метрике могут быть представлены графонами ; другая версия леммы регулярности просто утверждает, что пространство графонов компактно . ^[32]

• Комлос, Дж .; Симоновиц, М. (1996), «Лемма Семереди о регулярности и ее приложения в теории графов», Комбинаторика, Паулю Эрдешу восемьдесят, Vol. 2 (Кестхей, 1993) , Боляи Соц. Математика. Студ., вып. 2, Янош Бояи Матем. Soc., Будапешт, стр.  295–352 , MR  1395865..
• Komlós, J. ; Shokoufandeh, Ali; Simonovits, Miklós ; Szemerédi, Endre (2002), "The regularity lemma and its applications in graph theory", Theoretical aspects of computer science (Tehran, 2000) , Lecture Notes in Computer Science , vol. 2292, Springer, Berlin, pp.  84– 112, doi :10.1007/3-540-45878-6_3, ISBN 978-3-540-43328-6, MR  1966181.

• Эдмондс, Челси; Куцуку-Аргираки, Ангелики; Полсон, Лоуренс К. Лемма регулярности Семереди (Формальное доказательство развития в Isabelle/HOL, Архив формальных доказательств)