Элемент симметрии
В химии и кристаллографии элемент симметрии — это точка , линия или плоскость, относительно которых могут выполняться операции симметрии . В частности, элемент симметрии может быть плоскостью зеркала , осью вращения (как собственной, так и несобственной) или центром инверсии . [1] [2] [3] Для такого объекта, как молекула или кристалл , элемент симметрии соответствует набору операций симметрии, которые являются жесткими преобразованиями, использующими элемент симметрии, которые оставляют объект неизменным. Набор, содержащий эти операции, образует одну из групп симметрии объекта. Элементы этой группы симметрии не следует путать с самим «элементом симметрии». Грубо говоря, элемент симметрии — это геометрический набор неподвижных точек операции симметрии. Например, при вращении вокруг оси точки на оси не движутся, а при отражении точки, которые остаются неизменными, составляют плоскость симметрии.
Личность
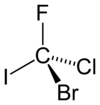
Элемент симметрии тождественности присутствует во всех объектах и обозначается E. [4] Он соответствует операции ничего не делать с объектом. Поскольку каждая молекула неотличима от самой себя, если с ней ничего не делать, каждый объект обладает по крайней мере элементом тождественности. Объект , не имеющий элементов симметрии, отличных от E, называется асимметричным. Такой объект обязательно хиральный. [5]

Молекула бромхлорфториодометана асимметрична: у нее нет симметрий, кроме идентичности.
Зеркальные плоскости
Зеркальные плоскости обозначаются как σ . В молекуле, которая также имеет ось симметрии, зеркальная плоскость, которая включает ось, называется вертикальной зеркальной плоскостью и обозначается σ v , в то время как перпендикулярная оси называется горизонтальной зеркальной плоскостью и обозначается σ h . Вертикальная зеркальная плоскость, которая делит пополам угол между двумя осями C2, называется двугранной зеркальной плоскостью, σ d . [6]

Вращательная симметрия
Вращательная симметрия, также известная как радиальная симметрия, представлена осью, вокруг которой вращается объект в соответствующей ему операции симметрии. Группа собственных вращений обозначается как C n , где степень вращения, восстанавливающая объект, составляет 360/n ( C 2 = вращение на 180º, C 3 = вращение на 120º, C 4 = вращение на 90º, C 5 = вращение на 72º). [4] Обозначение C n также используется для связанной, более абстрактной, циклической группы .
Неправильное вращение — это композиция вращения вокруг оси и отражения в плоскости, перпендикулярной этой оси. [2] Порядок, в котором выполняются вращение и отражение, не имеет значения (то есть эти операции коммутируют). Неправильное вращение также определяется как композиция вращения вокруг оси и инверсии вокруг точки на оси. [3] Эти определения эквивалентны, поскольку инверсия вокруг точки эквивалентна вращению на 180° вокруг любой оси с последующим зеркальным отражением относительно плоскости, перпендикулярной этой оси. Элементами симметрии для неправильного вращения являются ось вращения и либо плоскость зеркала, либо точка инверсии, либо и то, и другое. Группа неправильного вращения порядка 2 n обозначается S 2 n .
Инверсия
Для инверсии, обозначаемой i , в центре объекта должна быть точка, которая является центром инверсии. Инверсия состоит из прохождения каждой точки через центр инверсии и на то же расстояние с другой стороны молекулы. В операции инверсии для трехмерных координат центром инверсии является начало координат (0,0,0). Когда объект инвертируется, вектор положения точки в объекте, ⟨x,y,z⟩, инвертируется в ⟨-x,-y,-z⟩.
Галерея
- Пример вертикальной зеркальной плоскости.
- Молекула ферроцена , объект, имеющий симметрию S 10. Элементами ее симметрии являются: вертикальная ось вращения, горизонтальная плоскость и точка инверсии в центре.
Смотрите также
Ссылки
- ↑ Роберт Г. Мортимер (10 июня 2005 г.). Математика для физической химии. Academic Press. стр. 276–. ISBN 978-0-08-049288-9.
- ^ ab "Элемент симметрии". Онлайн-словарь кристаллографии . 2021-09-25 . Получено 2021-09-25 .
- ^ ab Wolff, PM de; et al. (1989). «Определение элементов симметрии в пространственных группах и точечных группах. Отчет Специального комитета Международного союза кристаллографии по номенклатуре симметрии». Acta Crystallographica Section A. 45 ( 7): 494–499. doi : 10.1107/S0108767389002230 . ISSN 0108-7673 . Получено 29.09.2021 .
- ^ ab Бернс, Джеральд; Глейзер, AM (2013). Пространственные группы для ученых, изучающих твердое тело . Elsevier. doi :10.1016/c2011-0-05712-5. ISBN 978-0-12-394400-9.
- ^ Аткинс, Питер (2006). ФИЗИЧЕСКАЯ ХИМИЯ АТКИНСА . Опубликовано в Великобритании Oxford University Press: WH Freeman and Company. стр. 405. ISBN 0-7167-8759-8.
- ^ Смарт, Лесли (2005). Химия твердого тела: введение. Элейн Мур (3-е изд.). Бока-Ратон: CRC Press. ISBN 0-7487-7516-1. OCLC 56661923.