Изображение сверхвысокого разрешения
Любая технология, позволяющая улучшить разрешение системы визуализации за пределы обычных пределов.

Визуализация сверхвысокого разрешения ( SR ) — это класс методов, которые улучшают (увеличивают) разрешение системы формирования изображений . В оптическом SR дифракционный предел систем преодолевается, в то время как в геометрическом SR улучшается разрешение цифровых датчиков формирования изображений .

В некоторых приложениях радиолокационной и гидролокационной визуализации (например, магнитно-резонансная томография (МРТ), компьютерная томография высокого разрешения ) для достижения SR по сравнению со стандартным алгоритмом периодограммы используются методы, основанные на подпространственной декомпозиции (например, MUSIC [1] ) и алгоритмы, основанные на сжатом измерении (например, SAMV [2] ) .

Методы получения изображений сверхвысокого разрешения используются в общей обработке изображений и в микроскопии сверхвысокого разрешения .

Основные понятия

Поскольку некоторые идеи, связанные с суперразрешением, поднимают фундаментальные вопросы, необходимо с самого начала рассмотреть соответствующие физические и информационно-теоретические принципы:

  • Дифракционный предел : Детали физического объекта, которые оптический прибор может воспроизвести на изображении, имеют пределы, которые предписаны законами физики, будь то сформулированные уравнениями дифракции в волновой теории света [3] или эквивалентно принципу неопределенности для фотонов в квантовой механике . [4] Передача информации никогда не может быть увеличена за пределы этой границы, но пакеты за пределами пределов могут быть ловко заменены (или мультиплексированы) на некоторые внутри него. [5] Дифракционный предел не столько «нарушается», сколько «обходится». Новые процедуры исследования электромагнитных возмущений на молекулярном уровне (в так называемом ближнем поле) [6] остаются полностью соответствующими уравнениям Максвелла .
    • Пространственно-частотная область: краткое выражение предела дифракции дается в пространственно-частотной области. В Фурье-оптике распределения света выражаются как суперпозиции ряда решетчатых световых узоров в диапазоне ширины полос, технически пространственных частот . Обычно учат, что теория дифракции предусматривает верхний предел, граничную пространственную частоту, за пределами которой элементы узора не переносятся в оптическое изображение, т. е. не разрешаются. Но на самом деле то, что устанавливает теория дифракции, является шириной полосы пропускания, а не фиксированным верхним пределом. Никакие законы физики не нарушаются, когда полоса пространственных частот за граничной пространственной частотой заменяется на полосу внутри нее: это давно реализовано в микроскопии темного поля . Информационно-теоретические правила не нарушаются и при наложении нескольких полос [7] [8] [9], их разделение на полученном изображении требует допущения об инвариантности объекта при многократной экспозиции, т. е. замены одного вида неопределенности другим.
  • Информация : Когда термин «сверхразрешение» используется в методах извлечения деталей объекта из статистической обработки изображения в пределах стандартного разрешения, например, усреднение нескольких экспозиций, он подразумевает обмен одного вида информации (извлечение сигнала из шума) на другой (предположение, что цель осталась неизменной).
  • Разрешение и локализация: Истинное разрешение подразумевает различение того, является ли цель, например, звезда или спектральная линия, одиночной или двойной, что обычно требует разделяемых пиков на изображении. Когда известно, что цель одиночная, ее местоположение можно определить с большей точностью, чем ширина изображения, путем нахождения центроида (центра тяжести) распределения света на ее изображении. Для этого процесса было предложено слово «ультраразрешение» [10], но оно не прижилось, и процедура высокоточной локализации обычно называется «суперразрешением».

Технические достижения в области повышения производительности устройств формирования и считывания изображений, которые в настоящее время классифицируются как устройства сверхвысокого разрешения, используются в полной мере, но всегда остаются в рамках, установленных законами физики и теорией информации.

Методы

Оптическое или дифракционное сверхразрешение

Замена полос пространственных частот: Хотя полоса пропускания, допустимая дифракцией, фиксирована, ее можно расположить в любом месте спектра пространственных частот. Примером может служить темнопольное освещение в микроскопии. См. также синтез апертуры .

Техника "структурированного освещения" сверхразрешения связана с муаровыми узорами . Цель, полоса тонких полос (верхний ряд), находится за пределами дифракционного предела. Когда полоса несколько более грубых разрешаемых полос (второй ряд) искусственно накладывается, комбинация (третий ряд) содержит компоненты муара , которые находятся в пределах дифракционного предела и, следовательно, содержатся в изображении (нижний ряд), что позволяет предположить наличие тонких полос, даже если они сами не представлены на изображении.

Мультиплексирование пространственно-частотных диапазонов

Изображение формируется с использованием обычной полосы пропускания оптического устройства. Затем некоторая известная структура света, например, набор световых полос, которые даже не обязательно должны быть в пределах полосы пропускания, накладывается на цель. [8] [9] Изображение теперь содержит компоненты, полученные в результате комбинации цели и наложенной световой структуры, например, муаровые полосы , и несет информацию о деталях цели, которую простое неструктурированное освещение не дает. Однако «сверхразрешенные» компоненты необходимо распутать, чтобы их можно было обнаружить. Например, см. структурированное освещение (рисунок слева).

Использование нескольких параметров в пределах традиционного дифракционного предела

Если у цели нет особых свойств поляризации или длины волны, два состояния поляризации или неперекрывающиеся области длин волн могут быть использованы для кодирования деталей цели, одно в полосе пространственной частоты внутри предела отсечки, другое за его пределами. Оба будут использовать обычную передачу полосы пропускания, но затем будут отдельно декодироваться для воссоздания структуры цели с расширенным разрешением.

Зондирование электромагнитных возмущений ближнего поля

Обычное обсуждение сверхразрешения включало обычное получение изображения объекта с помощью оптической системы. Но современные технологии позволяют исследовать электромагнитное возмущение в пределах молекулярных расстояний от источника [6] , что имеет превосходные свойства разрешения, см. также затухающие волны и разработку новой сверхразрешающей линзы .

Геометрическое или сверхвысокое разрешение обработки изображений

По сравнению с одним изображением, испорченным шумом во время его получения или передачи (слева), отношение сигнал/шум улучшается за счет подходящей комбинации нескольких отдельно полученных изображений (справа). Это может быть достигнуто только в пределах внутренней разрешающей способности процесса формирования изображения для выявления таких деталей.

Подавление шума на многоэкспозиционном изображении

Когда изображение ухудшается шумом, в среднем по многим экспозициям может быть больше деталей, даже в пределах дифракционного предела. См. пример справа.

Устранение размытия в отдельных кадрах

Известные дефекты в данной ситуации получения изображения, такие как расфокусировка или аберрации , иногда могут быть полностью или частично смягчены с помощью подходящей пространственно-частотной фильтрации даже одного изображения. Все такие процедуры остаются в пределах полосы пропускания, предписанной дифракцией, и не расширяют ее.

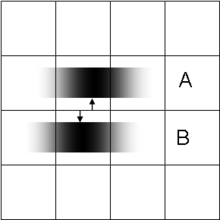
Оба объекта охватывают область размером более 3 пикселей, но в разной степени, что позволяет локализовать их с точностью, превосходящей размер пикселя.

Локализация субпиксельного изображения

Местоположение одного источника можно определить, вычислив «центр тяжести» ( центроид ) распределения света, простирающегося на несколько соседних пикселей (см. рисунок слева). При условии, что света достаточно, этого можно достичь с произвольной точностью, намного лучшей, чем ширина пикселя детектирующего прибора и предел разрешения для решения о том, является ли источник одиночным или двойным. Эта техника, которая требует предположения, что весь свет исходит из одного источника, лежит в основе того, что стало известно как микроскопия сверхвысокого разрешения , например, стохастическая оптическая реконструкционная микроскопия (STORM), где флуоресцентные зонды, прикрепленные к молекулам, дают информацию о расстоянии в наномасштабе . Это также механизм, лежащий в основе зрительной гиперостроты . [11]

Байесовская индукция за пределами традиционного дифракционного предела

Некоторые характеристики объекта, хотя и находящиеся за пределами дифракционного предела, могут быть известны как связанные с другими характеристиками объекта, которые находятся в пределах и, следовательно, содержатся в изображении. Затем, используя статистические методы, можно сделать выводы из имеющихся данных изображения о наличии полного объекта. [12] Классическим примером является предложение Торальдо ди Франчиа [13] о том, является ли изображение изображением одиночной или двойной звезды, путем определения того, превышает ли его ширина разброс от одиночной звезды. Этого можно достичь на расстояниях значительно ниже классических границ разрешения и требует предварительного ограничения на выбор «одиночная или двойная?»

Подход может принимать форму экстраполяции изображения в частотной области, предполагая, что объект является аналитической функцией , и что мы можем точно знать значения функции в некотором интервале . Этот метод серьезно ограничен постоянно присутствующим шумом в цифровых системах формирования изображений, но он может работать для радаров , астрономии , микроскопии или магнитно-резонансной томографии . [14] Совсем недавно был предложен быстрый алгоритм сверхвысокого разрешения для одного изображения, основанный на решении задач в замкнутой форме, и было продемонстрировано, что он значительно ускоряет большинство существующих байесовских методов сверхвысокого разрешения. [15] ℓ 2 − ℓ 2 {\displaystyle \ell _{2}-\ell _{2}}

Алиасинг

Геометрические алгоритмы реконструкции SR возможны тогда и только тогда, когда входные изображения с низким разрешением были недостаточно дискретизированы и, следовательно, содержат алиасинг . Из-за этого алиасинга высокочастотный контент желаемого изображения реконструкции встроен в низкочастотный контент каждого из наблюдаемых изображений. При наличии достаточного количества изображений наблюдения, и если набор наблюдений изменяется по своей фазе (т. е. если изображения сцены смещены на величину субпикселя), то информация о фазе может быть использована для отделения алиасированного высокочастотного контента от истинного низкочастотного контента, и изображение с полным разрешением может быть точно реконструировано. [16]

На практике этот частотный подход не используется для реконструкции, но даже в случае пространственных подходов (например, слияние методом сдвига и добавления [17] ) наличие наложения спектров по-прежнему является необходимым условием для реконструкции SR.

Технические реализации

Существует множество вариантов SR как с одним кадром, так и с несколькими кадрами. Многокадровый SR использует субпиксельные сдвиги между несколькими изображениями с низким разрешением одной и той же сцены. Он создает изображение с улучшенным разрешением, объединяя информацию из всех изображений с низким разрешением, и созданные изображения с более высоким разрешением лучше описывают сцену. Методы однокадрового SR пытаются увеличить изображение, не создавая размытости. Эти методы используют другие части изображений с низким разрешением или другие несвязанные изображения, чтобы предположить, как должно выглядеть изображение с высоким разрешением. Алгоритмы также можно разделить по их домену: частотному или пространственному домену . Первоначально методы сверхвысокого разрешения хорошо работали только на изображениях в градациях серого, [18] но исследователи нашли методы адаптации их к изображениям с цветной камеры. [17] Недавно также было показано использование сверхвысокого разрешения для 3D-данных. [19]

Исследовать

Существуют перспективные исследования по использованию глубоких сверточных сетей для достижения сверхвысокого разрешения. [20] В частности, была продемонстрирована работа, показывающая преобразование 20-кратного микроскопического изображения пыльцевых зерен в 1500-кратное сканирующее электронное изображение с его помощью. [21] Хотя этот метод может увеличить информационное содержание изображения, нет никакой гарантии, что увеличенные характеристики присутствуют в исходном изображении, и глубокие сверточные масштабирующие устройства не следует использовать в аналитических приложениях с неоднозначными входными данными. [22] [23] Эти методы могут искажать характеристики изображения, что может сделать их небезопасными для медицинского использования. [24]

Смотрите также

Ссылки

  1. ^ Шмидт, РО, «Определение местоположения множественных излучателей и оценка параметров сигнала», IEEE Trans. Antennas Propagation, том AP-34 (март 1986 г.), стр. 276-280.
  2. ^ Абейда, Хабти; Чжан, Цилинь; Ли, Цзянь ; Мерабтин, Наджим (2013). «Итеративные разреженные асимптотические подходы на основе минимальной дисперсии для обработки массивов» (PDF) . Труды IEEE по обработке сигналов . 61 (4): 933–944. arXiv : 1802.03070 . Bibcode : 2013ITSP...61..933A. doi : 10.1109/tsp.2012.2231676. ISSN  1053-587X. S2CID  16276001.
  3. ^ Борн М., Вольф Э., Принципы оптики , Cambridge Univ. Press, любое издание
  4. ^ Фокс М., 2007 Квантовая оптика Оксфорд
  5. ^ Залевский З., Мендлович Д. 2003 Оптическое сверхразрешение Springer
  6. ^ ab Betzig, E; Trautman, JK (1992). «Оптика ближнего поля: микроскопия, спектроскопия и модификация поверхности за пределами дифракционного предела». Science . 257 (5067): 189–195. Bibcode :1992Sci...257..189B. doi :10.1126/science.257.5067.189. PMID  17794749. S2CID  38041885.
  7. ^ Lukosz, W., 1966. Оптические системы с разрешающей способностью, превышающей классический предел. J. opt. soc. Am. 56, 1463–1472.
  8. ^ ab Guerra, John M. (1995-06-26). "Сверхразрешение через освещение дифракционно-рожденными затухающими волнами". Applied Physics Letters . 66 (26): 3555–3557. Bibcode : 1995ApPhL..66.3555G. doi : 10.1063/1.113814. ISSN  0003-6951.
  9. ^ ab Gustaffsson, M., 2000. Преодоление предела латерального разрешения в два раза с использованием структурированной иллюминационной микроскопии. J. Microscopy 198, 82–87.
  10. ^ Кокс, И.Дж., Шеппард, К.Дж.Р., 1986. Информационная емкость и разрешение в оптической системе. J.opt. Soc. Am. A 3, 1152–1158
  11. ^ Вестхаймер, Г. (2012). «Оптическое сверхразрешение и повышенная острота зрения». Prog Retin Eye Res . 31 (5): 467–80. doi : 10.1016/j.preteyeres.2012.05.001 . PMID  22634484.
  12. ^ Харрис, Дж. Л., 1964. Разрешающая сила и принятие решений. J. opt. soc. Am. 54, 606–611.
  13. ^ Торальдо ди Франсия, Г., 1955. Разрешающая сила и информация. Ж. опт. соц. Являюсь. 45, 497–501.
  14. ^ Д. Пут, Б. Юриссен, Ю. Бастиенсен, Дж. Вераарт, В. Ван Хек, П. М. Паризель и Дж. Сийберс, «Сверхразрешение для многосрезовой диффузионной тензорной визуализации», Магнитный резонанс в медицине, (2012)
  15. ^ Н. Чжао, Ц. Вэй, А. Басараб, Н. Добижон, Д. Куаме и Дж. Й. Турнере, «Быстрое сверхвысокое разрешение одиночных изображений с использованием нового аналитического решения для задач ℓ 2 − ℓ 2 {\displaystyle \ell _{2}-\ell _{2}}», IEEE Trans. Image Process., 2016, ожидается в печати.
  16. ^ J. Simpkins, RL Stevenson, "Введение в сверхразрешающую визуализацию". Математическая оптика: классические, квантовые и вычислительные методы, под ред. V. Lakshminarayanan, M. Calvo и T. Alieva. CRC Press, 2012. 539-564.
  17. ^ ab S. Farsiu, D. Robinson, M. Elad и P. Milanfar, «Быстрое и надежное многокадровое сверхразрешение», IEEE Transactions on Image Processing, т. 13, № 10, стр. 1327–1344, октябрь 2004 г.
  18. ^ П. Чизман, Б. Канефски, Р. Крафт и Дж. Штутц, 1994
  19. ^ S. Schuon, C. Theobalt, J. Davis и S. Thrun, «LidarBoost: сверхвысокое разрешение по глубине для сканирования трехмерных форм методом ToF», в трудах IEEE CVPR 2009
  20. ^ Джонсон, Джастин; Алахи, Александр; Фей-Фей, Ли (2016-03-26). «Потери восприятия при передаче стиля в реальном времени и сверхразрешении». arXiv : 1603.08155 [cs.CV].
  21. ^ Грант-Джейкоб, Джеймс А.; Маккей, Бенита С.; Бейкер, Джеймс АГ.; Кси, Юньхуэй; Хит, Дэниел Дж.; Локсхэм, Мэтью; Исон, Роберт У.; Миллс, Бен (18.06.2019). «Нейронная линза для биологической визуализации сверхвысокого разрешения». Journal of Physics Communications . 3 (6): 065004. Bibcode : 2019JPhCo...3f5004G. doi : 10.1088/2399-6528/ab267d . ISSN  2399-6528.
  22. ^ Блау, Йохай; Михаэли, Томер (2018). Компромисс между восприятием и искажением . Конференция IEEE по компьютерному зрению и распознаванию образов. стр. 6228–6237. arXiv : 1711.06077 . doi : 10.1109/CVPR.2018.00652.
  23. ^ Zeeberg, Amos (2023-08-23). ​​«Инструменты ИИ, делающие изображения лучше». Журнал Quanta . Получено 2023-08-28 .
  24. ^ Коэн, Джозеф Пол; Лак, Марго; Хонари, Сина (2018). «Потери соответствия распределений могут вызывать галлюцинации при переводе медицинских изображений». В Алехандро Ф. Франги; Джулия А. Шнабель; Христос Давацикос; Карлос Альберола-Лопес; Габор Фихтингер (ред.). Медицинские вычисления изображений и компьютерное вмешательство – MICCAI 2018. 21-я международная конференция, Гранада, Испания, 16–20 сентября 2018 г., Труды, часть I. Лекционные заметки по информатике. Том 11070. стр. 529–536. arXiv : 1805.08841 . doi :10.1007/978-3-030-00928-1_60. ISBN 978-3-030-00927-4. S2CID  43919703 . Получено 1 мая 2022 г. .
  • Кертис, Крейг Х.; Милстер, Том Д. (октябрь 1992 г.). «Анализ сверхразрешения в магнитооптических устройствах хранения данных». Прикладная оптика . 31 (29): 6272–6279. Bibcode : 1992ApOpt..31.6272M. doi : 10.1364/AO.31.006272. PMID  20733840.
  • Залевский, З.; Мендлович, Д. (2003). Оптическое сверхразрешение . Springer. ISBN 978-0-387-00591-1.
  • Caron, JN (сентябрь 2004 г.). «Быстрая супервыборка многокадровых последовательностей с использованием слепой деконволюции». Optics Letters . 29 (17): 1986–1988. Bibcode :2004OptL...29.1986C. doi :10.1364/OL.29.001986. PMID  15455755.
  • Клемент, ГТ; Хуттунен, Дж.; Хайнинен, К. (2005). «Сверхчеткое ультразвуковое изображение с использованием реконструкции с обратной проекцией». Журнал Акустического общества Америки . 118 (6): 3953–3960. Bibcode : 2005ASAJ..118.3953C. doi : 10.1121/1.2109167. PMID  16419839.
  • Geisler, WS; Perry, JS (2011). "Статистика для оптимального прогнозирования точек на естественных изображениях". Journal of Vision . 11 (12): 14. doi : 10.1167/11.12.14 . PMC  5144165. PMID  22011382 .
  • Cheung, V.; Frey, BJ; Jojic, N. (20–25 июня 2005 г.). Видеократкие обзоры (PDF) . Конференция по компьютерному зрению и распознаванию образов (CVPR). Том 1. стр. 42–49. doi :10.1109/CVPR.2005.366.
  • Бертеро, М.; Боккаччи, П. (октябрь 2003 г.). «Сверхразрешение в вычислительной визуализации». Micron . 34 (6–7): 265–273. doi :10.1016/s0968-4328(03)00051-9. PMID  12932769.
  • Борман, С.; Стивенсон, Р. (1998). «Улучшение пространственного разрешения последовательностей изображений с низким разрешением – всесторонний обзор с направлениями будущих исследований» (технический отчет) . Университет Нотр-Дам.
  • Борман, С.; Стивенсон, Р. (1998). Суперразрешение из последовательностей изображений — обзор (PDF) . Симпозиум Среднего Запада по схемам и системам.
  • Park, SC; Park, MK; Kang, MG (май 2003 г.). «Реконструкция изображений со сверхвысоким разрешением: технический обзор». Журнал обработки сигналов IEEE . 20 (3): 21–36. Bibcode : 2003ISPM...20...21P. doi : 10.1109/MSP.2003.1203207. S2CID  12320918.
  • Фарсиу, С.; Робинсон, Д.; Элад, М.; Миланфар, П. (август 2004 г.). «Достижения и проблемы в области сверхвысокого разрешения». Международный журнал систем и технологий визуализации . 14 (2): 47–57. doi :10.1002/ima.20007. S2CID  12351561.
  • Элад, М.; Хел-Ор, И. (август 2001 г.). «Быстрый алгоритм реконструкции сверхвысокого разрешения для чистого поступательного движения и общего пространственно-инвариантного размытия». Труды IEEE по обработке изображений . 10 (8): 1187–1193. Bibcode : 2001ITIP...10.1187E. CiteSeerX  10.1.1.11.2502 . doi : 10.1109/83.935034. PMID  18255535.
  • Ирани, М.; Пелег, С. (июнь 1990 г.). Суперразрешение из последовательностей изображений (PDF) . Международная конференция по распознаванию образов. Том 2. С. 115–120.
  • Sroubek, F.; Cristobal, G.; Flusser, J. (2007). «Унифицированный подход к сверхразрешению и многоканальной слепой деконволюции». IEEE Transactions on Image Processing . 16 (9): 2322–2332. Bibcode : 2007ITIP...16.2322S. doi : 10.1109/TIP.2007.903256. PMID  17784605. S2CID  6367149.
  • Калабуиг, Алехандро; Мико, Висенте; Гарсия, Хавьер; Залевски, Зеев; Феррейра, Карлос (март 2011 г.). «Интерферометрическая микроскопия с суперразрешением и одиночной экспозицией с использованием мультиплексирования красного–зеленого–синего». Optics Letters . 36 (6): 885–887. Bibcode :2011OptL...36..885C. doi :10.1364/OL.36.000885. PMID  21403717.
  • Чан, Вай-Сан; Лам, Эдмунд; Нг, Майкл К.; Мак, Джузеппе Й. (сентябрь 2007 г.). «Реконструкция со сверхвысоким разрешением в вычислительной системе формирования изображений сложного глаза». Многомерные системы и обработка сигналов . 18 (2–3): 83–101. doi :10.1007/s11045-007-0022-3. S2CID  16452552.
  • Ng, Michael K.; Shen, Huanfeng; Lam, Edmund Y.; Zhang, Liangpei (2007). "Алгоритм реконструкции сверхвысокого разрешения на основе регуляризации полной вариации для цифрового видео". Журнал EURASIP об успехах в обработке сигналов . 2007 : 074585. Bibcode : 2007EJASP2007..104N. doi : 10.1155/2007/74585 . hdl : 10722/73871 .
  • Гласнер, Д.; Бэгон, С.; Ирани, М. (октябрь 2009 г.). Суперразрешение из одного изображения (PDF) . Международная конференция по компьютерному зрению (ICCV).; "пример и результаты".
  • Ben-Ezra, M.; Lin, Zhouchen; Wilburn, B.; Zhang, Wei (июль 2011 г.). «Penrose Pixels for Super-Resolution» (PDF) . IEEE Transactions on Pattern Analysis and Machine Intelligence . 33 (7): 1370–1383. CiteSeerX  10.1.1.174.8804 . doi :10.1109/TPAMI.2010.213. PMID  21135446. S2CID  184868.
  • Берлинер, Л.; Буффа, А. (2011). «Сверхразрешающая визуализация с переменной дозой в цифровой рентгенографии: качество и снижение дозы с помощью плоскопанельного флюороскопического детектора». Int J Comput Assist Radiol Surg . 6 (5): 663–673. doi :10.1007/s11548-011-0545-9. PMID  21298404.
  • Тимофте, Р.; Де Смет, В.; Ван Гул, Л. (ноябрь 2014 г.). A+: Регрессия скорректированной закрепленной окрестности для быстрого сверхразрешения (PDF) . 12-я Азиатская конференция по компьютерному зрению (ACCV).; "коды и данные".
  • Хуан, Дж.-Б.; Сингх, А.; Ахуджа, Н. (июнь 2015 г.). Суперразрешение отдельных изображений из преобразованных самообразцов . Конференция IEEE по компьютерному зрению и распознаванию образов .; "страница проекта".
  • CHRISTENSEN-JEFFRIES, T.; COUTURE, O.; DAYTON, PA; ELDAR, YC; HYNYNEN, K.; KIESSLING, F.; O'REILLY, M.; PINTON, GF; SCHMITZ, G.; TANG, M.-X.; TANTER, M.; VAN SLOUN, RJG (2020). "Ультразвуковая визуализация сверхвысокого разрешения". Ultrasound Med. Biol . 46 (4): 865–891. doi : 10.1016/j.ultrasmedbio.2019.11.013 . PMC  8388823. PMID  31973952 .


Взято с "https://en.wikipedia.org/w/index.php?title=Сверхразрешающая_изображение&oldid=1253361306"