Расстройство
В комбинаторной математике расстройство — это перестановка элементов множества , в которой ни один элемент не появляется в своей исходной позиции. Другими словами, расстройство — это перестановка, которая не имеет неподвижных точек .
Число расстройств множества размера n известно как субфакториал n или n - ое число расстройств или n -ое число де Монмора (в честь Пьера Ремона де Монмора ). Обозначения для субфакториалов в общем использовании включают ! n , D n , d n или n ¡ . [a] [1] [2]
Для n > 0 субфакториал ! n равен ближайшему целому числу к n !/ e , где n ! обозначает факториал n , а e ≈ 2,718281828... — число Эйлера . [3]
Проблема подсчета отклонений была впервые рассмотрена Пьером Раймоном де Монмором в его «Очерке анализа азартных игр» [4] в 1708 году; он решил ее в 1713 году, как и Николай Бернулли примерно в то же время.
Пример

Предположим, что профессор дал тест 4 студентам — A, B, C и D — и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколькими способами профессор может вернуть тесты студентам для проверки, так чтобы ни один студент не получил свой собственный тест обратно? Из 24 возможных перестановок (4!) для возврата тестов,
АБВГД , АБ , округ Колумбия, А ЦБ Д , А ЦКБ, А DBC, А Д С Б, BA CD , БАДК , БСА D , BCDA , БДАК , БД С А, КАБИНА D , КАДБ , С Б А Д , С Б ДА, ЦДАБ , ЦДБА , ДАБК , ДА С Б, Д Б АС, Д БК А, ДКАБ , DCBA .
есть только 9 нарушений (показаны синим курсивом выше). В каждой другой перестановке этого набора из 4 членов, по крайней мере, один студент получает свой собственный тест обратно (показаны жирным красным).
Другая версия проблемы возникает, когда мы спрашиваем, сколькими способами n писем, каждое из которых адресовано разным лицам, можно поместить в n конвертов с заранее проставленным адресом так, чтобы ни одно письмо не оказалось в конверте с правильным адресом.
Подсчет расстройств
Подсчет расстройств множества сводится к задаче о шляпе-чеке , в которой рассматривается количество способов, которыми n шляп (назовем их от h 1 до h n ) могут быть возвращены n людям ( от P 1 до P n ) таким образом, что ни одна шляпа не вернется к своему владельцу. [5]
Каждый человек может получить любую из n − 1 шляп, которая не является его собственной. Назовем шляпу, которую получает человек P 1 , h i и сочтем ее владельцем : P i получает либо шляпу P 1 , h 1 , либо какую-то другую. Соответственно, задача распадается на два возможных случая:
- P i получает шляпу, отличную от h 1 . Этот случай эквивалентен решению задачи с n − 1 людьми и n − 1 шляпами, поскольку для каждого из n − 1 людей, кроме P 1 , есть ровно одна шляпа из оставшихся n − 1 шляп, которые они могут не получить (для любого P j , кроме P i , неполучаемая шляпа — это h j , тогда как для P i это h 1 ). Другой способ увидеть это — переименовать h 1 в h i , где расстройство более явное: для любого j от 2 до n , P j не может получить h j .
- P i получает h 1. В этом случае проблема сводится к n − 2 людям и n − 2 шляпам, поскольку P 1 получил шляпу своего i , а P i получил шляпу своего h 1 , что фактически исключает их дальнейшее рассмотрение.
Для каждой из n − 1 шляп, которые может получить P 1 , количество способов, которыми P 2 , ..., P n могут получить шляпы, равно сумме подсчетов для двух случаев.
Это дает нам решение проблемы «шляпной чеки»: выражаясь алгебраически, число ! n расстройств множества из n элементов равно для , где и [6]
Количество нарушений малой длины приведено в таблице ниже.
| н | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ! н | 1 | 0 | 1 | 2 | 9 | 44 | 265 | 1,854 | 14,833 | 133,496 | 1,334,961 | 14,684,570 | 176,214,841 | 2,290,792,932 |
Существуют различные другие выражения для ! n , эквивалентные формуле, приведенной выше. Они включают в себя для и
- для
где — ближайшая целочисленная функция , а — функция пола . [3] [6]
Другие связанные формулы включают [3] [7] и
Также имеет место следующее повторение: [6]
Вывод по принципу включения-исключения
Можно также вывести нерекурсивную формулу для числа расстройств n -множества. Для мы определяем быть множеством перестановок n объектов, которые фиксируют k -й объект. Любое пересечение коллекции i этих множеств фиксирует определенный набор из i объектов и, следовательно, содержит перестановки. Такие коллекции существуют , поэтому принцип включения-исключения дает и поскольку расстройство является перестановкой, которая не оставляет ни одного из n объектов фиксированным, это подразумевает
С другой стороны, поскольку мы можем выбрать n - i элементов, которые будут находиться на своих местах, и нарушить порядок других i элементов всего ! i способами, по определению. [8]
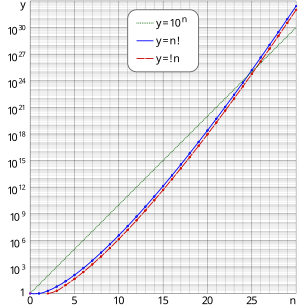
Рост числа расстройств по меренприближается к ∞
Из и путем подстановки немедленно получаем, что Это предел вероятности того , что случайно выбранная перестановка большого числа объектов является расстройством. Вероятность сходится к этому пределу чрезвычайно быстро с ростом n , поэтому ! n является ближайшим целым числом к n !/ e . Приведенный выше полулогарифмический график показывает, что график расстройства отстает от графика перестановки на почти постоянную величину.
Более подробную информацию об этом расчете и указанном выше пределе можно найти в статье о статистике случайных перестановок .
Асимптотическое разложение по числам Белла
Асимптотическое разложение для числа расстройств в терминах чисел Белла выглядит следующим образом: где - любое фиксированное положительное целое число, а обозначает -е число Белла . Более того, константа, подразумеваемая большим O -членом, не превышает . [9]
Обобщения
Задача о встречах заключается в том, сколько перестановок множества размера n имеют ровно k неподвижных точек.
Расстройства являются примером более широкого поля ограниченных перестановок. Например, задача о менажах спрашивает, если n пар противоположного пола сидят за столом мужчина-женщина-мужчина-женщина-..., сколькими способами их можно рассадить так, чтобы никто не сидел рядом со своим партнером?
Более формально, если заданы множества A и S , а также некоторые множества U и V сюръекций A → S , мы часто хотим узнать количество пар функций ( f , g ) таких, что f принадлежит U , а g принадлежит V , и для всех a из A , f ( a ) ≠ g ( a ); другими словами, где для каждого f и g существует нарушение φ множества S , такое, что f ( a ) = φ( g ( a )).
Другим обобщением является следующая проблема:
- Сколько существует анаграмм без фиксированных букв данного слова?
Например, для слова, состоящего всего из двух различных букв, скажем, из n букв A и m букв B, ответ, конечно, 1 или 0 в зависимости от того, n = m или нет, поскольку единственный способ образовать анаграмму без фиксированных букв — это поменять все A на B , что возможно, если и только если n = m . В общем случае для слова с n 1 буквой X 1 , n 2 буквами X 2 , ..., n r буквами X r оказывается (после надлежащего использования формулы включения-исключения ), что ответ имеет вид для определенной последовательности многочленов P n , где P n имеет степень n . Но приведенный выше ответ для случая r = 2 дает отношение ортогональности, откуда P n являются многочленами Лагерра ( с точностью до знака, который легко определяется). [10]

В частности, для классических расстройств имеем, что где — верхняя неполная гамма-функция .
Сложность вычислений
Определение того, содержит ли данная группа перестановок (описываемая данным набором перестановок, которые ее порождают) какие-либо нарушения, является NP-полной задачей . [11] [12]
Таблица значений факториала и отклонения Перестановки, Расстройства, 0 1 =1×10 0
1 =1×10 0
= 1 1 1 =1×10 0
0 = 0 2 2 =2×10 0
1 =1×10 0
= 0,5 3 6 =6×10 0
2 =2×10 0
≈0,33333 33333 4 24 =2,4×10 1
9 =9×10 0
= 0,375 5 120 =1,20×10 2
44 =4,4×10 1
≈0,36666 66667 6 720 =7,20×10 2
265 =2,65×10 2
≈0,36805 55556 7 5,040 =5,04×10 3
1,854 ≈1,85×10 3
≈0.36785,71429 8 40,320 ≈4,03×10 4
14,833 ≈1,48×10 4
≈0,36788 19444 9 362,880 ≈3,63×10 5
133,496 ≈1,33×10 5
≈0.36787 91887 10 3,628,800 ≈3,63×10 6
1,334,961 ≈1,33×10 6
≈0.36787 94643 11 39,916,800 ≈3,99×10 7
14,684,570 ≈1,47×10 7
≈0.36787 94392 12 479,001,600 ≈4,79×10 8
176,214,841 ≈1,76×10 8
≈0,36787 94413 13 6,227,020,800 ≈6,23×10 9
2,290,792,932 ≈2,29×10 9
≈0,36787 94412 14 87,178,291,200 ≈8,72×10 10
32,071,101,049 ≈3,21×10 10
≈0,36787 94412 15 1,307,674,368,000 ≈1,31×10 12
481,066,515,734 ≈4,81×10 11
≈0,36787 94412 16 20,922,789,888,000 ≈2,09×10 13
7,697,064,251,745 ≈7,70×10 12
≈0,36787 94412 17 355,687,428,096,000 ≈3,56×10 14
130,850,092,279,664 ≈1,31×10 14
≈0,36787 94412 18 6,402,373,705,728,000 ≈6,40×10 15
2,355,301,661,033,953 ≈2,36×10 15
≈0,36787 94412 19 121,645,100,408,832,000 ≈1,22×10 17
44,750,731,559,645,106 ≈4,48×10 16
≈0,36787 94412 20 2,432,902,008,176,640,000 ≈2,43×10 18
895,014,631,192,902,121 ≈8,95×10 17
≈0,36787 94412 21 51,090,942,171,709,440,000 ≈5,11×10 19
18,795,307,255,050,944,540 ≈1,88×10 19
≈0,36787 94412 22 1,124,000,727,777,607,680,000 ≈1,12×10 21
413,496,759,611,120,779,881 ≈4,13×10 20
≈0,36787 94412 23 25 852 016 738 884 976 640 000 ≈2,59×10 22
9,510,425,471,055,777,937,262 ≈9,51×10 21
≈0,36787 94412 24 620 448 401 733 239 439 360 000 ≈6,20×10 23
228 250 211 305 338 670 494 289 ≈2,28×10 23
≈0,36787 94412 25 15 511 210 043 330 985 984 000 000 ≈1,55×10 25
5706255282633466762357224 ≈5,71×10 24
≈0,36787 94412 26 403 291 461 126 605 635 584 000 000 ≈4,03×10 26
148 362 637 348 470 135 821 287 825 ≈1,48×10 26
≈0,36787 94412 27 10 888 869 450 418 352 160 768 000 000 ≈1,09×10 28
4 005 791 208 408 693 667 174 771 274 ≈4,01×10 27
≈0,36787 94412 28 304 888 344 611 713 860 501 504 000 000 ≈3,05×10 29
112 162 153 835 443 422 680 893 595 673 ≈1,12×10 29
≈0,36787 94412 29 8 841 761 993 739 701 954 543 616 000 000 ≈8,84×10 30
3 252 702 461 227 859 257 745 914 274 516 ≈3,25×10 30
≈0,36787 94412 30 265 252 859 812 191 058 636 308 480 000 000 ≈2,65×10 32
97 581 073 836 835 777 732 377 428 235 481 ≈9,76×10 31
≈0,36787 94412
Сноски
- ^ Название «субфакториал» берет свое начало от Уильяма Аллена Уитворта . [1]
Ссылки
- ^ ab Cajori, Florian (2011). История математических обозначений: два тома в одном. Cosimo, Inc. стр. 77. ISBN 9781616405717– через Google.
- ^ Грэм, Рональд Л.; Кнут, Дональд Э .; Паташник, Орен (1994). Конкретная математика . Рединг, Массачусетс: Addison–Wesley. ISBN 0-201-55802-5.
- ^ abc Hassani, Mehdi (2003). «Расстройства и приложения». Журнал целочисленных последовательностей . 6 (1). Статья 03.1.2. Bibcode :2003JIntS...6...12H – через cs.uwaterloo.ca.
- ^ де Монмор, PR (1713) [1708]. Essay d'analyse sur les jeux de Risk (на французском языке) (Revue & augmentée de plusieurs Lettres, второе изд.). Париж, Франция: Жак Кийо (1708 г.) / Жак Кийо (1713 г.).
- ^ Сковилл, Ричард (1966). «Проблема шляпы и чека». American Mathematical Monthly . 73 (3): 262– 265. doi :10.2307/2315337. JSTOR 2315337.
- ^ abc Стэнли, Ричард (2012). Перечислительная комбинаторика, том 1 (2-е изд.). Cambridge University Press. Пример 2.2.1. ISBN 978-1-107-60262-5.
- ^ Вайсштейн, Эрик В. «Субфакториал». MathWorld .
- ^ Bizley, MTL (май 1967). «Заметка о расстройствах». Math. Gaz . 51 (376): 118– 120. doi :10.2307/3614384. JSTOR 3614384.
- ^ Хассани, М. «Расстройства и чередующиеся суммы перестановок путем интегрирования». J. Integer Seq. 23, статья 20.7.8, 1–9, 2020
- ^ Even, S.; Gillis, J. (1976). «Расстройства и полиномы Лагерра». Математические труды Кембриджского философского общества . 79 (1): 135– 143. Bibcode :1976MPCPS..79..135E. doi :10.1017/S0305004100052154. S2CID 122311800 . Получено 27 декабря 2011 г. .
- ^ Любив, Анна (1981). «Некоторые NP-полные проблемы, похожие на изоморфизм графов». SIAM Journal on Computing . 10 (1): 11– 21. doi :10.1137/0210002. MR 0605600.
- ^ Бабай, Ласло (1995). «Группы автоморфизмов, изоморфизм, реконструкция». Справочник по комбинаторике (PDF) . Том 1, 2. Амстердам, Нидерланды: Elsevier. Гл. 27, стр. 1447–1540. MR 1373683 – через cs.uchicago.edu.
Внешние ссылки
- Баез, Джон (2003). «Давайте сойдем с ума!» (PDF) – через math.ucr.edu.
- Богарт, Кеннет П.; Дойл, Питер Г. (1985). «Несексистское решение проблемы менаж» – через math.dartmouth.edu.
- Вайсштейн, Э.В. «Психоз». MathWorld / Wolfram Research – через mathworld.wolfram.com.






![{\displaystyle !n=\left[{\frac {n!}{e}}\right]=\left\lfloor {\frac {n!}{e}}+{\frac {1}{2}}\right\rfloor }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d522701b28d640964b2e50f781b9e10c385898f5)

![{\displaystyle \left[x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee30b48da3d61e9dfa898ca4d209afdcc6503dc)




























