Анализ прочности и напряжений

Анализ прочности на напряжение — это анализ прочности материалов и интерференции напряжений, приложенных к материалам, где «материалы» не обязательно являются сырьем или деталями, но могут быть целой системой. Анализ прочности на напряжение — это инструмент, используемый в технике надежности .

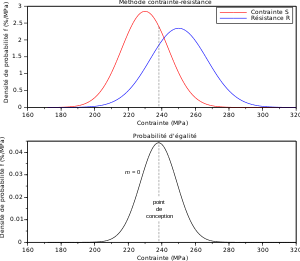
Напряжения окружающей среды имеют распределение со средним значением и стандартным отклонением , а прочность компонентов имеет распределение со средним значением и стандартным отклонением . Перекрытие этих распределений является вероятностью отказа . Это перекрытие также называется интерференцией напряжения и прочности.${\displaystyle \left(\mu _{x}\right)}$ ${\displaystyle \left(s_{x}\right)}$${\displaystyle \left(\mu _{y}\right)}$${\displaystyle \left(s_{y}\right)}$${\displaystyle \left(Z\right)}$

Если распределения как напряжения, так и прочности следуют нормальному распределению, то надежность (R) компонента можно определить с помощью следующего уравнения: ^[1] , где${\displaystyle R=1-P(Z)}$

${\displaystyle Z=-{\frac {\mu _{y}-\mu _{x}}{\sqrt {s_{x}^{2}+s_{y}^{2}}}}}$

P(Z) можно определить с помощью таблицы Z или статистического программного обеспечения.

• Метод надежности первого порядка

• http://reliawiki.org/index.php/Stress-Strength_Anaанализ
• http://www.engr.iupui.edu/me/courses/stressstrengthinterference.pdf