Теорема Сиаччи

В кинематике ускорение частицы, движущейся по кривой в пространстве, является производной по времени от ее скорости. В большинстве приложений вектор ускорения выражается как сумма его нормальной и тангенциальной компонент , которые ортогональны друг другу. Теорема Сиаччи, сформулированная итальянским математиком Франческо Сиаччи (1839–1907), представляет собой кинематическое разложение вектора ускорения на его радиальную и тангенциальную компоненты. В общем случае радиальная и тангенциальная компоненты не ортогональны друг другу. Теорема Сиаччи особенно полезна в движениях, где угловой момент постоянен.

Теорема Сиаччи на плоскости

Движение частицы P в плоскости.

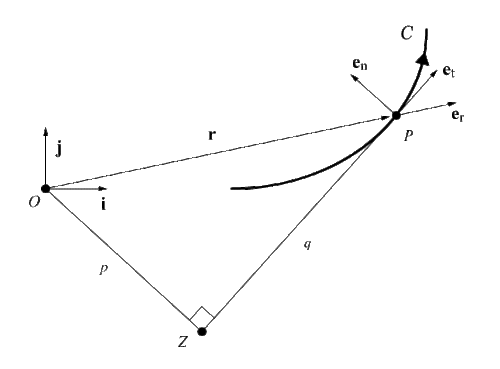
Пусть частица P массы m   движется в двумерном евклидовом пространстве (плоское движение). Предположим, что C — кривая, вычерченная P , а s — длина дуги C, соответствующая времени t . Пусть O — произвольное начало координат на плоскости, а { i , j } — фиксированный ортонормированный базис . Вектор положения частицы равен

г = г е г . {\displaystyle \mathbf {r} =r\mathbf {e} _ {r}.}

Единичный вектор e r является радиальным базисным вектором полярной системы координат в плоскости. Вектор скорости частицы равен

в = г г г т = с ˙ е т = в е т , {\displaystyle \mathbf {v} = {\frac {d\mathbf {r} {dt}} = {\dot {s}} \mathbf {e} _ {t} = v\mathbf {e} _{ т},}

где e t — единичный касательный вектор к C. Определим момент импульса P как

час = г × м в = час к , {\displaystyle \mathbf {h} =\mathbf {r} \times m\mathbf {v} =h\mathbf {k} ,}

где k = i x j . Предположим, что h ≠ 0 . Тогда вектор положения r может быть выражен как

г = д е т − п е н {\displaystyle \mathbf {r} =q\mathbf {e} _{t}-p\mathbf {e} _{n}}

в базисе Серре-Френе { e t , e n , e b }. Величина момента импульса равна h = mpv , где p — перпендикуляр из начала координат на касательную ZP . Согласно теореме Сиаччи, ускорение a точки P можно выразить как

а = − к в 2 г п е г + ( час 2 ) ′ 2 п 2 е т = С г е г + С т е т . {\displaystyle \mathbf {a} =- {\frac {\kappa v^{2}r}{p}}\mathbf {e} _{r}+{\frac {(h^{2})'} {2p^{2}}}\mathbf {e} _{t}=S_{r}\mathbf {e} _{r}+S_{t}\mathbf {e} _{t}.}

где штрих обозначает дифференциацию по длине дуги s , а κ — функция кривизны кривой C. В общем случае S r и S t не равны ортогональным проекциям a на e r и e t .

Пример: Центральные силы

Предположим, что момент импульса частицы P является ненулевой константой и что S r является функцией r . Тогда

С г = − ф ( г ) = − к г час 2 п 3 , С т = 0. {\displaystyle S_{r}=-f(r)=-{\frac {\kappa rh^{2}}{p^{3}}},\qquad S_{t}=0.}

Поскольку кривизна в точке орбиты определяется выражением

к = 1 г г п г г , {\displaystyle \kappa = {\frac {1}{r}}{\frac {dp}{dr}},}

Функцию f удобно записать в виде ОДУ первого порядка

ф ( г ) = час 2 п 3 г п г г . {\displaystyle f(r)={\frac {h^{2}}{p^{3}}}{\frac {dp}{dr}}.}

Уравнение сохранения энергии для частицы получается тогда, если f ( r ) интегрируема.

1 2 час 2 п 2 + ∫ ф ( г ) = с о н с т а н т . {\displaystyle {\frac {1}{2}}{\frac {h^{2}}{p^{2}}}+\int f(r)=\mathrm {constant} .}

Теорема Сиаччи в пространстве

Теорему Сиаччи можно распространить на трехмерные движения. Таким образом, пусть C — пространственная кривая, вычерченная точкой P , а s — длина дуги C, соответствующая времени t . Также предположим, что бинормальная компонента момента импульса не обращается в нуль. Тогда вектор ускорения точки P можно выразить как

а = − к в 2 г п е г + ( в г в г с + к в 2 д п ) е т . {\displaystyle \mathbf {a} =- {\frac {\kappa v^{2}r}{p}}\mathbf {e} _{r}+\left(v{\frac {dv}{ds} }+{\frac {\kappa v^{2}q}{p}}\right)\mathbf {e} _{t}.}

Тангенциальная составляющая касается кривой C. Радиальная составляющая направлена ​​от точки P к точке, где перпендикуляр из произвольного фиксированного начала координат пересекает соприкасающуюся плоскость . Другие выражения для a можно найти в [1] , где дано новое доказательство теоремы Сиаччи.

Смотрите также

Ссылки

  1. ^ Кейси, Джеймс (2011). «Разрешение Сиаччи вектора ускорения для пространственной кривой». Meccanica . 46 (2): 471–476. doi : 10.1007/s11012-010-9296-x .
  • Ф. Сиаччи. Мото для линейного плана. Атти делла Реале, Туринская академия наук, XIV, 750–760, 1879.
  • Ф. Сиаччи. Мото для одной линии игры. Атти делла Реале Туринская академия наук, XIV, 946–951, 1879.
  • ET Whittaker . Трактат об аналитической динамике частиц и твердых тел . 4-е издание, Cambridge University Press, Кембридж. Перепечатано Dover Publications, Inc., Нью-Йорк (1944).
  • Натанаэль Гроссман. Чистая радость небесной механики. Биркхойзер, Базель, 1996.
Взято с "https://en.wikipedia.org/w/index.php?title=Siacci%27s_theorem&oldid=1182183668"