Полулогарифмический график


В науке и технике полулогарифмический график или полулогарифмический график имеет одну ось в логарифмическом масштабе , другую в линейном масштабе . Это полезно для данных с экспоненциальными отношениями , где одна переменная охватывает большой диапазон значений. [ 1]
Все уравнения этой формы образуют прямые линии, если их построить в полулогарифмическом масштабе, поскольку взятие логарифмов обеих сторон дает
Это линия с наклоном и вертикальным пересечением. Логарифмическая шкала обычно обозначается в десятичной системе счисления; иногда в двухлинейной системе счисления:
Логарифмически -линейный (иногда логарифмически-линевый) график имеет логарифмическую шкалу по оси y и линейную шкалу по оси x ; линейно-логарифмический (иногда линально-логарифмический) график имеет противоположное значение. Наименование — выход-вход ( y – x ), обратный порядок ( x , y ).
На полулогарифмическом графике интервал шкалы на оси y (или оси x ) пропорционален логарифму числа, а не самому числу. Это эквивалентно преобразованию значений y (или значений x ) в их логарифм и построению данных на линейной шкале. Логарифмический график использует логарифмическую шкалу для обеих осей и, следовательно, не является полулогарифмическим графиком.
Уравнения
Уравнение линии на линейно-логарифмическом графике, где ось абсцисс масштабируется логарифмически (с основанием логарифма n ), будет иметь вид
Уравнение линии на логарифмически-линейном графике с осью ординат , масштабированной в логарифмическом масштабе (с основанием логарифма n ), будет иметь вид:
Нахождение функции из полулогарифмического графика
Линейно-логарифмический график
На линейно-логарифмическом графике выберите некоторую фиксированную точку ( x 0 , F 0 ), где F 0 — это сокращение для F ( x 0 ), где-нибудь на прямой линии на приведенном выше графике, а затем некоторую другую произвольную точку ( x 1 , F 1 ) на том же графике. Формула наклона графика:
что приводит к
или
что означает, что
Другими словами, F пропорциональна логарифму x , умноженному на наклон прямой линии ее графика lin–log, плюс константа. В частности, прямая линия на графике lin–log, содержащая точки ( F 0 , x 0 ) и ( F 1 , x 1 ), будет иметь функцию:
логарифмически линейный график
На логарифмически-линейном графике (логарифмическая шкала по оси y) выберите некоторую фиксированную точку ( x 0 , F 0 ), где F 0 — это сокращение от F ( x 0 ), где-нибудь на прямой линии на приведенном выше графике, а затем некоторую другую произвольную точку ( x 1 , F 1 ) на том же графике. Формула наклона графика:
что приводит к
Обратите внимание, что n log n ( F 1 ) = F 1 . Поэтому журналы можно инвертировать, чтобы найти:
или
Это можно обобщить для любой точки, а не только для F 1 :
Примеры из реальной жизни
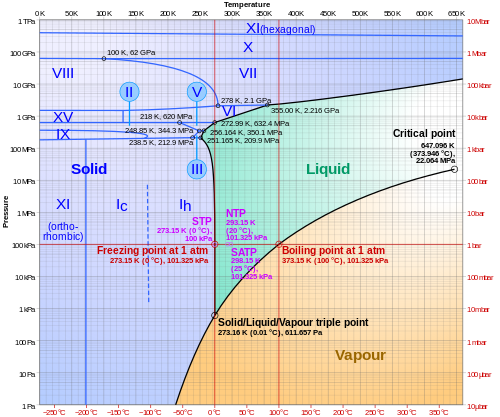
Фазовая диаграмма воды
В физике и химии график логарифма давления в зависимости от температуры можно использовать для иллюстрации различных фаз вещества, как в следующем примере для воды :
Развитие "свиного гриппа" в 2009 году
Хотя наиболее распространенной основой является «десять» , бывают случаи, когда более уместны другие основы, как в этом примере: [ необходимы дополнительные пояснения ]

Обратите внимание, что горизонтальная (временная) ось линейна, с равномерно распределенными датами, вертикальная (случаи) ось логарифмическая, с равномерно распределенными делениями, помеченными последовательными степенями двойки. Полулогарифмический график позволяет легче увидеть, когда инфекция перестала распространяться с максимальной скоростью, т. е. прямая линия на этом экспоненциальном графике, и начинает изгибаться, указывая на более медленную скорость. Это может указывать на то, что работает какая-то форма смягчающих действий, например, социальное дистанцирование.
Рост микроорганизмов
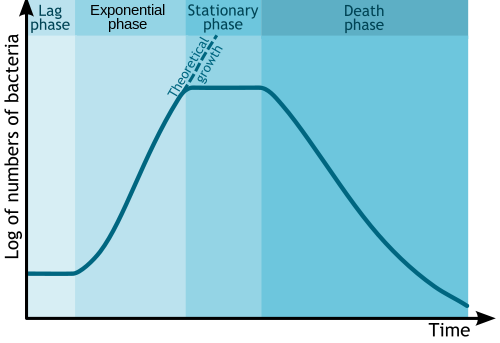
В биологии и биологической инженерии изменение численности микробов вследствие бесполого размножения и истощения питательных веществ обычно иллюстрируется полулогарифмическим графиком. Время обычно является независимой осью, а логарифм числа или массы бактерий или других микробов — зависимой переменной. Это формирует график с четырьмя отдельными фазами, как показано ниже.
Смотрите также
- Номограмма , более сложные графики
- Нелинейная регрессия#Преобразование , для преобразования нелинейной формы в полулогарифмическую форму, пригодную для неитеративного вычисления.
- Логарифмический график
Ссылки
- ^ (1) Bourne, M. "Graphs on Logarithmic and Semi-Logarithmic Paper". Интерактивная математика . www.intmath.com. Архивировано из оригинала 6 августа 2021 г. Получено 26 октября 2021 г.
(2) Борн, Мюррей (25 января 2007 г.). «Интересный полулогарифмический график – рейтинг трафика YouTube». SquareCirclez: блог IntMath . www.intmath.com. Архивировано из оригинала 26 февраля 2021 г. Получено 26 октября 2021 г.












![{\displaystyle F(x)=(F_{1}-F_{0}){\left[{\frac {\log _{n}(x/x_{0})}{\log _{n}(x_{1}/x_{0})}}\right]}+F_{0}=(F_{1}-F_{0})\log _{\frac {x_{1}}{x_{0}}}{\left({\frac {x}{x_{0}}}\right)}+F_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da143562dac9e25d0e2a741861ef66bb7077d6f6)




