Салинон

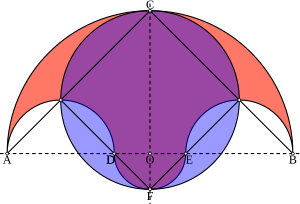
Сальон (что означает «солонка» на греческом языке) — геометрическая фигура , состоящая из четырех полукругов . Впервые она была введена в « Книге лемм» , работе, приписываемой Архимеду . [ ^1]

Пусть A , D , E , и B будут четырьмя точками на прямой в плоскости, в указанном порядке, с AD = EB . Пусть O будет биссектрисой отрезка AB (и DE ). Нарисуйте полуокружности выше прямой AB с диаметрами AB , AD , и EB , и еще одну полуокружность ниже с диаметром DE . Сальон — это фигура, ограниченная этими четырьмя полуокружностями. ^[2]

Архимед ввел салинон в своей Книге лемм , применив Книгу II, Предложение 10 «Начал » Евклида . Архимед заметил, что «площадь фигуры, ограниченной окружностями всех полукругов, [равна] площади круга на CF как диаметре». ^[3]

А именно, если — радиус большого охватывающего полукруга, а — радиус малого центрального полукруга, то площадь салинона равна: ^[4]${\displaystyle r_{1}}$${\displaystyle r_{2}}$$${\displaystyle A={\frac {1}{4}}\пи \left(r_{1}+r_{2}\right)^{2}.}$$

Если бы точки D и E сошлись с точкой O , то образовался бы арбелос , еще одно творение Архимеда, с симметрией относительно оси Y. [ ^3]

• Луна Гиппократа

• Л'Арбелос. Часть II, автор Хамза Хелиф, www.images.math.cnrs.fr, CNRS.