Функция Розенброка
Функция, используемая в качестве задачи проверки производительности для алгоритмов оптимизации
График функции Розенброка двух переменных. Здесь , а минимальное значение нуля находится при . а = 1 , б = 100 {\displaystyle а=1,b=100} ( 1 , 1 ) {\displaystyle (1,1)}

В математической оптимизации функция Розенброка — это невыпуклая функция , введенная Говардом Х. Розенброком в 1960 году, которая используется в качестве задачи проверки производительности для алгоритмов оптимизации . [1] Она также известна как функция долины Розенброка или банана Розенброка .

Глобальный минимум находится внутри длинной, узкой, параболической -образной плоской долины. Найти долину тривиально. Сблизиться к глобальному минимуму, однако, сложно.

Функция определяется как

ф ( х , у ) = ( а − х ) 2 + б ( у − х 2 ) 2 {\displaystyle f(x,y)=(ax)^{2}+b(yx^{2})^{2}}

Она имеет глобальный минимум при , где . Обычно эти параметры задаются так, что и . Только в тривиальном случае, когда функция симметрична и минимум находится в начале координат. ( х , у ) = ( а , а 2 ) {\displaystyle (x,y)=(a,a^{2})} ф ( х , у ) = 0 {\displaystyle f(x,y)=0} а = 1 {\displaystyle а=1} б = 100 {\displaystyle b=100} а = 0 {\displaystyle а=0}

Многомерные обобщения

Обычно встречаются два варианта.

Анимация функции Розенброка трех переменных. [2]

Одна из них представляет собой сумму несвязанных двумерных задач Розенброка и определена только для четных s: Н / 2 {\displaystyle N/2} Н {\displaystyle N}

ф ( х ) = ф ( х 1 , х 2 , … , х Н ) = ∑ я = 1 Н / 2 [ 100 ( х 2 я − 1 2 − х 2 я ) 2 + ( х 2 я − 1 − 1 ) 2 ] . {\displaystyle f(\mathbf {x} )=f(x_{1},x_{2},\dots ,x_{N})=\sum _{i=1}^{N/2}\left[100(x_{2i-1}^{2}-x_{2i})^{2}+(x_{2i-1}-1)^{2}\right].} [3]

Этот вариант имеет предсказуемо простые решения.

Второй, более сложный вариант —

ф ( х ) = ∑ я = 1 Н − 1 [ 100 ( х я + 1 − х я 2 ) 2 + ( 1 − х я ) 2 ] где х = ( х 1 , … , х Н ) ∈ Р Н . {\displaystyle f(\mathbf {x} )=\sum _{i=1}^{N-1}[100(x_{i+1}-x_{i}^{2})^{2}+(1-x_{i})^{2}]\quad {\mbox{где}}\quad \mathbf {x} =(x_{1},\ldots ,x_{N})\in \mathbb {R} ^{N}.} [4]

имеет ровно один минимум для (при ) и ровно два минимума для — глобальный минимум при и локальный минимум вблизи . Этот результат получается путем установки градиента функции равным нулю, заметив, что полученное уравнение является рациональной функцией . Для малых многочлены могут быть определены точно, и теорема Штурма может быть использована для определения числа действительных корней , в то время как корни могут быть ограничены в области . [5] Для больших этот метод перестает работать из-за размера задействованных коэффициентов. Н = 3 {\displaystyle N=3} ( 1 , 1 , 1 ) {\displaystyle (1,1,1)} 4 ≤ Н ≤ 7 {\displaystyle 4\leq N\leq 7} ( 1 , 1 , . . . , 1 ) {\displaystyle (1,1,...,1)} х ^ = ( − 1 , 1 , … , 1 ) {\displaystyle {\hat {\mathbf {x} }}=(-1,1,\dots ,1)} х {\displaystyle x} Н {\displaystyle N} | х я | < 2.4 {\displaystyle |x_{i}|<2.4} Н {\displaystyle N}

Стационарные точки

Многие из стационарных точек функции демонстрируют регулярную структуру при построении графика. [5] Эту структуру можно использовать для их определения.

Корни Розенброка, имеющие горбовидную структуру

Примеры оптимизации

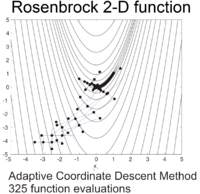
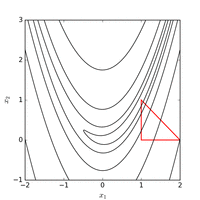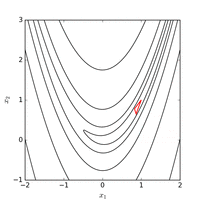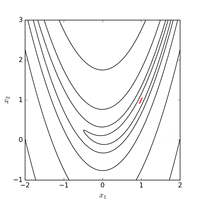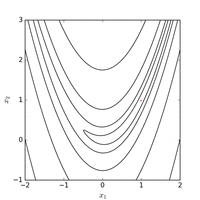
Функция Розенброка Нелдера-Мида
Метод Нелдера-Мида, примененный к функции Розенброка

Функция Розенброка может быть эффективно оптимизирована путем адаптации соответствующей системы координат без использования какой-либо информации о градиенте и без построения локальных аппроксимационных моделей (в отличие от многих оптимизаторов без производных). На следующем рисунке показан пример оптимизации двумерной функции Розенброка путем адаптивного спуска по координатам от начальной точки . Решение со значением функции может быть найдено после 325 оценок функции. х 0 = ( − 3 , − 4 ) {\displaystyle x_{0}=(-3,-4)} 10 − 10 {\displaystyle 10^{-10}}

Используя метод Нелдера–Мида из начальной точки с регулярным начальным симплексом, найден минимум со значением функции после 185 оценок функции. Рисунок ниже визуализирует эволюцию алгоритма. х 0 = ( − 1 , 1 ) {\displaystyle x_{0}=(-1,1)} 1.36 ⋅ 10 − 10 {\displaystyle 1.36\cdot 10^{-10}}

Смотрите также

Ссылки

  1. ^ Розенброк, ХХ (1960). «Автоматический метод нахождения наибольшего или наименьшего значения функции». The Computer Journal . 3 (3): 175–184. doi : 10.1093/comjnl/3.3.175 . ISSN  0010-4620.
  2. ^ Симионеску, П.А. (2014). Инструменты компьютерного моделирования и построения графиков для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.
  3. ^ Диксон, Л. К. У.; Миллс, Д. Дж. (1994). «Влияние ошибок округления на метод переменной метрики». Журнал теории оптимизации и ее применения . 80 : 175–179. doi : 10.1007/BF02196600.
  4. ^ "Обобщенная функция Розенброка" . Получено 2008-09-16 .
  5. ^ ab Kok, Schalk; Sandrock, Carl (2009). «Расположение и характеристика стационарных точек расширенной функции Розенброка». Evolutionary Computation . 17 (3): 437–53. doi :10.1162/evco.2009.17.3.437. hdl : 2263/13845 . PMID  19708775.
Взято с "https://en.wikipedia.org/w/index.php?title=Rosenbrock_function&oldid=1248348139"