Алгоритм обратного удаления

Алгоритм обратного удаления — это алгоритм в теории графов, используемый для получения минимального остовного дерева из заданного связного графа с весовыми рёбрами . Впервые он появился в работе Крускала (1956), но его не следует путать с алгоритмом Крускала , который появляется в той же статье. Если граф несвязен, этот алгоритм найдёт минимальное остовное дерево для каждой несвязной части графа. Набор этих минимальных остовных деревьев называется минимальным остовным лесом, который содержит каждую вершину в графе.

Этот алгоритм является жадным алгоритмом , выбирающим наилучший выбор в любой ситуации. Он является обратным алгоритму Крускала , который является другим жадным алгоритмом для поиска минимального остовного дерева. Алгоритм Крускала начинается с пустого графа и добавляет ребра, в то время как алгоритм обратного удаления начинается с исходного графа и удаляет из него ребра. Алгоритм работает следующим образом:

• Начнем с графа G, который содержит список ребер E.
• Пройдитесь по E в порядке убывания веса ребер.
• Для каждого ребра проверьте, не приведет ли удаление ребра к дальнейшему разрыву графа.
• Выполняйте любое удаление, которое не приводит к дополнительному отключению.

Функция ReverseDelete ( edges[] E ) сортирует  E в порядке убывания  Определить индекс i ← 0 while  i < size ( E ) do Определить ребро ← E [ i ] удалить  E [ i ] если граф не связен , то  E [ i ] ← ребро  i ← i + 1 возвратные ребра[] E

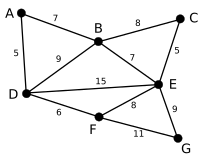
На рисунке выше граф представляет собой множество ребер E , каждое ребро которого содержит вес и соединенные вершины v1 и v2 .

В следующем примере алгоритм оценивает зеленые края, а красные края удаляются.

	Это наш исходный график. Числа около ребер указывают вес ребер.
	Алгоритм начнет работу с ребра с максимальным весом, которым в данном случае является DE с весом ребра 15. Поскольку удаление ребра DE не приводит к дальнейшему разрыву графа, оно удаляется.
	Следующее по величине ребро — FG , поэтому алгоритм проверит, приведет ли удаление этого ребра к дальнейшему разъединению графа. Поскольку удаление ребра не приведет к дальнейшему разъединению графа, ребро затем удаляется.
	Следующим по величине ребром является ребро BD, поэтому алгоритм проверит это ребро и удалит его.
	Следующим ребром для проверки является ребро EG , которое не будет удалено, поскольку оно отключит узел G от графа. Поэтому следующим ребром для удаления является ребро BC .
	Следующим по величине ребром является ребро EF , поэтому алгоритм проверит это ребро и удалит его.
	Затем алгоритм выполнит поиск по оставшимся ребрам и не найдет другого ребра для удаления; таким образом, это окончательный граф, возвращаемый алгоритмом.

Можно показать, что алгоритм работает за время O ( E log V (log log V ) ³ ) (используя нотацию big-O ), где E — количество ребер, а V — количество вершин. Эта граница достигается следующим образом:

• Сортировка ребер по весу с использованием сортировки сравнением занимает O ( E log E ) времени, что можно упростить до O ( E log V ), учитывая тот факт, что наибольшее возможное E равно V ² .
• Существует E итераций цикла.
• Удаление ребра, проверка связности полученного графа и (если он отключен) повторная вставка ребра могут быть выполнены за время O (log V (log log V ) ³ ) на операцию (Thorup 2000).

Рекомендуется сначала прочитать доказательство алгоритма Крускала .

Доказательство состоит из двух частей. Во-первых, доказывается, что оставшиеся после применения алгоритма ребра образуют остовное дерево. Во-вторых, доказывается, что остовное дерево имеет минимальный вес.

Оставшийся подграф (g), полученный алгоритмом, не является несвязным, поскольку алгоритм проверяет это в строке 7. Результирующий подграф не может содержать цикл, поскольку если он это делает, то при движении по ребрам мы столкнемся с максимальным ребром в цикле и удалим это ребро. Таким образом, g должен быть остовным деревом основного графа G.

Покажем, что следующее предложение P истинно по индукции: если F — множество ребер, оставшихся в конце цикла while, то существует некоторое минимальное остовное дерево, которое (его ребра ) является подмножеством F.

1. Очевидно, что P выполняется до начала цикла while. Поскольку взвешенный связный граф всегда имеет минимальное остовное дерево и поскольку F содержит все ребра графа, то это минимальное остовное дерево должно быть подмножеством F.
2. Теперь предположим, что P истинно для некоторого неконечного множества ребер F , и пусть T — минимальное остовное дерево, которое содержится в F. Мы должны показать, что после удаления ребра e в алгоритме существует некоторое (возможно, другое) остовное дерево T', которое является подмножеством F.
   1. если следующее удаленное ребро e не принадлежит T, то T=T' является подмножеством F и выполняется P.
   2. в противном случае, если e принадлежит T: сначала отметим, что алгоритм удаляет только те ребра, которые не вызывают несвязность в F. поэтому e не вызывает несвязность. Но удаление e вызывает несвязность в дереве T (так как оно является членом T). предположим, что e разделяет T на подграфы t1 и t2. Поскольку весь граф связан после удаления e, то должен существовать путь между t1 и t2 (отличный от e), поэтому должен существовать цикл C в F (до удаления e). теперь у нас должно быть другое ребро в этом цикле (назовем его f), которое не находится в T, но находится в F (так как если бы все ребра цикла были в дереве T, то оно больше не было бы деревом). теперь мы утверждаем, что T' = T - e + f является минимальным остовным деревом, которое является подмножеством F.
   3. Во-первых, мы докажем, что T' является остовным деревом . Мы знаем, что, удалив ребро в дереве и добавив другое ребро, которое не приводит к образованию цикла, мы получим другое дерево с теми же вершинами. Поскольку T было остовным деревом, T' также должно быть остовным деревом . Поскольку добавление "f" не приводит к образованию циклов, так как "e" удалено. (Обратите внимание, что дерево T содержит все вершины графа).
   4. во-вторых, мы доказываем, что T' является минимальным остовным деревом. У нас есть три случая для ребер "e" и "f". wt - весовая функция.
      1. wt( f ) < wt( e ) это невозможно, так как это приводит к тому, что вес дерева T' будет строго меньше T . Поскольку T является минимальным остовным деревом, это просто невозможно.
      2. wt( f ) > wt( e ) это также невозможно. поскольку тогда, когда мы проходим по ребрам в порядке убывания весов ребер, мы должны сначала увидеть « f ». поскольку у нас есть цикл C, удаление « f » не приведет к какой-либо несвязности в F. поэтому алгоритм удалил бы его из F раньше. поэтому « f » не существует в F, что невозможно (мы доказали, что f существует на шаге 4).
      3. поэтому wt(f) = wt(e), поэтому T' также является минимальным остовным деревом. поэтому снова выполняется P.
3. поэтому P выполняется, когда цикл while завершен (то есть когда мы увидели все ребра), и мы доказали в конце, что F становится остовным деревом , и мы знаем, что F имеет минимальное остовное дерево в качестве своего подмножества. поэтому F должно быть само по себе минимальным остовным деревом .

• Алгоритм Крускала
• Алгоритм Прима
• Алгоритм Борувки
• Алгоритм Дейкстры

• Кляйнберг, Джон; Тардос, Ева (2006), Разработка алгоритмов , Нью-Йорк: Pearson Education, Inc..
• Крускал, Джозеф Б. (1956), «О кратчайшем остовном поддереве графа и задаче коммивояжера», Труды Американского математического общества , 7 (1): 48– 50, doi : 10.2307/2033241 , JSTOR  2033241.
• Торуп, Миккель (2000), «Почти оптимальная полностью динамическая связность графа», Труды 32-го симпозиума ACM по теории вычислений , стр.  343–350 , doi :10.1145/335305.335345.