Пентадекагон

Правильный пентадекагон
Правильный пентадекагон
Тип	Правильный многоугольник
Ребра и вершины	15
Символ Шлефли	{15}
Диаграммы Кокстера–Дынкина
Группа симметрии	Двугранный (D 15 ), порядок 2×15
Внутренний угол ( градусы )	156°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии пентадекагон или пентакайдекагон или 15-угольник — это пятнадцатиугольник .

Правильный пентадекагон обозначается символом Шлефли {15} .

Правильный пятиугольник имеет внутренние углы 156 ° и длину стороны a , его площадь определяется выражением

${\displaystyle {\begin{aligned}A={\frac {15}{4}}a^{2}\cot {\frac {\pi }{15}}&={\frac {15}{4}}{\sqrt {7+2{\sqrt {5}}+2{\sqrt {15+6{\sqrt {5}}}}}}a^{2}\\&={\frac {15a^{2}}{8}}\left({\sqrt {3}}+{\sqrt {15}}+{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}\right)\\&\simeq 17.6424\,a^{2}.\end{aligned}}}$

Так как 15 = 3 × 5, произведение различных простых чисел Ферма , то правильный пентадекагон можно построить с помощью циркуля и линейки : Следующие построения правильных пентадекагонов с заданной описанной окружностью аналогичны иллюстрации предложения XVI в книге IV « Начал » Евклида . ^[1]

Сравните конструкцию по Евклиду на этом изображении: Пятиугольник

В построении для данной описанной окружности: — сторона равностороннего треугольника, — сторона правильного пятиугольника. ^[2] Точка делит радиус в золотом сечении :${\displaystyle {\overline {FG}}={\overline {CF}}{\text{,}}\;{\overline {AH}}={\overline {GM}}{\text{,}}\;|E_{1}E_{6}|}$${\displaystyle |E_{2}E_{5}|}$${\displaystyle H}$${\displaystyle {\overline {AM}}}$${\displaystyle {\frac {\overline {AH}}{\overline {HM}}}={\frac {\overline {AM}}{\overline {AH}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}}$

По сравнению с первой анимацией (с зелеными линиями) на следующих двух изображениях показаны две дуги окружности (для углов 36° и 24°), повернутые на 90° против часовой стрелки. Они не используют сегмент , а вместо этого используют сегмент как радиус для второй дуги окружности (угол 36°).${\displaystyle {\overline {CG}}}$${\displaystyle {\overline {MG}}}$${\displaystyle {\overline {AH}}}$

Построение циркулем и линейкой для данной длины стороны. Построение почти равно построению пятиугольника при данной стороне , затем представление продолжается путем расширения одной стороны и создает сегмент, здесь который делится в соответствии с золотым сечением:${\displaystyle {\overline {FE_{2}}}{\text{,}}}$

${\displaystyle {\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}}$

Радиус описанной окружности Длина стороны Угол${\displaystyle {\overline {E_{2}M}}=R\;;\;\;}$${\displaystyle {\overline {E_{1}E_{2}}}=a\;;\;\;}$${\displaystyle DE_{1}M=ME_{2}D=78^{\circ }}$

${\displaystyle {\begin{aligned}R&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)={\frac {1}{2}}\cdot {\sqrt {8+2\cdot {\sqrt {5}}+2{\sqrt {15+6\cdot {\sqrt {5}}}}}}\cdot a\\&={\frac {\sin(78^{\circ })}{\sin(24^{\circ })}}\cdot a\approx 2.40486\cdot a\end{aligned}}}$

Правильный пентадекагон имеет диэдральную симметрию Dih ₁₅ , порядок 30, представленную 15 линиями отражения. Dih ₁₅ имеет 3 диэдральные подгруппы: Dih ₅ , Dih ₃ и Dih ₁ . И еще четыре циклические симметрии: Z ₁₅ , Z ₅ , Z ₃ и Z ₁ , где Z _n представляет собой вращательную симметрию π/ n радиан.

На пентадекагоне существует 8 различных симметрий. Джон Конвей обозначает эти симметрии буквой, а порядок симметрии следует за буквой. ^[3] Он дает r30 для полной отражательной симметрии, Dih ₁₅ . Он дает d (диагональ) с линиями отражения через вершины, p с линиями отражения через ребра (перпендикулярно), а для нечетного пентадекагона i с зеркальными линиями через вершины и ребра, и g для циклической симметрии. a1 обозначает отсутствие симметрии.

Эти более низкие симметрии допускают степени свободы при определении неправильных пентадекагонов. Только подгруппа g15 не имеет степеней свободы, но может рассматриваться как направленные ребра .

Существует три правильных звездчатых многоугольника : {15/2}, {15/4}, {15/7}, построенные из тех же 15 вершин правильного пентадекагона, но соединенные путем пропуска каждой второй, четвертой или седьмой вершины соответственно.

Существуют также три правильные звездные фигуры : {15/3}, {15/5}, {15/6}, первая из которых представляет собой соединение трех пятиугольников , вторая — соединение пяти равносторонних треугольников , а третья — соединение трех пентаграмм .

Составную фигуру {15/3} можно условно рассматривать как двумерный эквивалент трехмерного соединения пяти тетраэдров .

Картина	{15/2}	{15/3} или 3{5}	{15/4}	{15/5} или 5{3}	{15/6} или 3{5/2}	{15/7}
Внутренний угол	132°	108°	84°	60°	36°	12°

Более глубокие усечения правильного пентадекагона и пентадекаграммы могут производить изогональные ( вершинно-транзитивные ) промежуточные формы звездчатого многоугольника с равноотстоящими вершинами и двумя длинами ребер. ^[4]

Вершинно-транзитивные усечения пентадекагона
Квазирегулярный	Изогональный							Квазирегулярный
т{15/2}={30/2}								т{15/13}={30/13}
т{15/7} = {30/7}								т{15/8}={30/8}
т{15/11}={30/22}								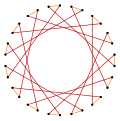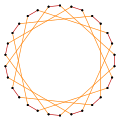т{15/4}={30/4}

Правильный пентадекагон — это многоугольник Петри для некоторых многогранников большей размерности, спроецированный в косоортогональной проекции :

14-симплекс (14D)

Правильный треугольник, десятиугольник и пентадекагон могут полностью заполнить плоскую вершину . Однако из-за нечетного числа сторон треугольника фигуры не могут чередоваться вокруг треугольника, поэтому вершина не может образовывать полуправильную мозаику .

• Построение пентадекагона по заданной длине стороны, вычисление радиуса описанной окружности R {\displaystyle R} (на немецком языке)
• Построение пентадекагона по заданной длине стороны, пример: радиус описанной окружности C G ¯ = R {\displaystyle {\overline {CG}}=R}

• Вайсштейн, Эрик В. «Пентадекагон». MathWorld .