Диаграмма Рэндольфа

Диаграмма Рэндольфа ( R-диаграмма ) — это простой способ визуализации логических выражений и комбинаций множеств. Диаграммы Рэндольфа были созданы математиком Джоном Ф. Рэндольфом в 1965 году во время его работы в Университете Арканзаса .

Диаграммы Рэндольфа проще всего интерпретировать, определяя каждую линию как принадлежащую или относящуюся к одному логическому утверждению или набору. Любая точка над линией указывает на истину или включение, а под линией указывает на ложность или исключение. Используя эту систему, можно представить любую комбинацию множеств или логических утверждений с помощью пересекающихся линий.

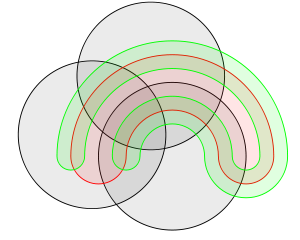
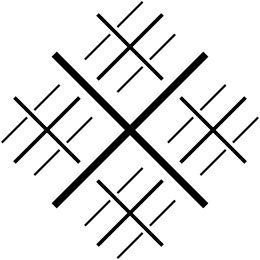
Хотя диаграммы Венна чаще используются для представления комбинаций множеств, диаграммы Рэндольфа имеют преимущество в том, что они могут четко представлять комбинации из более чем 3 множеств. Диаграммы Венна требуют либо расширения в более высокие пространственные измерения, либо использования более сложных форм, в то время как диаграммы Рэндольфа равномерно подразделяют для каждого дополнительного множества. ^[1] Вот сравнение между диаграммой Венна и R-диаграммой для 5 множеств логических утверждений:

В своей вводной статье по теме « Перекрестный допрос исчисления высказываний и операций над множествами » ^[2] Рэндольф упоминает, что первое использование крестиков и точек для представления логических отношений было введено У. С. МакКаллохом , нейрофизиологом и современником Рэндольфа. Рэндольф модифицировал систему МакКаллоха новым способом представления комбинаций и отношений более чем двух логических утверждений или множеств, а именно подразделением каждой секции R-диаграммы новой диагональной линией для каждого нового введенного элемента. Статья Рэндольфа предполагает, что его первоначальная идея состояла в использовании R-диаграмм для представления логических отношений, а затем расширил идею, применив ее также и к теории множеств. На протяжении всей статьи R-диаграммы используются в сочетании с обычными логическими и двоичными символами операций множеств.

При применении R-диаграмм к теории логики логические утверждения p, q и r могут стать линией или несколькими линиями, чтобы визуально отобразить действительность каждого элемента в более крупном утверждении. Обычно p представляется восходящей наклонной линией (/), а q — нисходящей наклонной линией (\). Точка на диаграмме над наклонной линией указывает на истинность этого утверждения; аналогично, точка под ней указывает на ложность. R-диаграммы для p и q показаны ниже соответственно:

Для более чем двух утверждений четыре пробела, образованные пересечением линий p и q, должны быть подразделены на большее количество линий. В случае r в каждом из четырех пробелов добавляется одна восходящая наклонная линия (/). R-диаграмма для r показана ниже:

Этот метод можно расширить для любого количества значений истинности:

, и т. д.

R-диаграммы в основном используются для представления логических выражений. При наличии логического предложения R-диаграммы способны отображать результат каждой возможной истинной/ложной вариации каждого элемента, создавая альтернативный способ представления таблицы истинности .

Все основные логические операции, или связки , можно выразить с помощью R-диаграмм как более удобной для чтения альтернативы таблице истинности, как показано в таблице ниже:

Базовые логические операции

Имя	Символы	R-диаграмма	Таблица истинности
Отрицание (не)	¬ , ~		п ¬п Т Ф Ф Т
Союз (и)	& , ∧		п д п ∧ д Т Т Т Т Ф Ф Ф Т Ф Ф Ф Ф
Дизъюнкция (или)	∨		п д п ∨ д Т Т Т Т Ф Т Ф Т Т Ф Ф Ф
Материальное значение (если...тогда)	${\displaystyle \rightarrow}$ , ,${\displaystyle \Стрелка вправо}$${\displaystyle \supset}$		п д п д${\displaystyle \rightarrow}$ Т Т Т Т Ф Ф Ф Т Т Ф Ф Т
Двуусловный (если и только если, xnor)	${\displaystyle \leftrightarrow}$, ,${\displaystyle \equiv}$${\displaystyle =}$		п д п д${\displaystyle \leftrightarrow}$ Т Т Т Т Ф Ф Ф Т Ф Ф Ф Т

R-диаграммы можно использовать для легкого упрощения сложных логических выражений, используя пошаговый процесс. Используя порядок операций, логические операторы применяются к R-диаграммам в правильной последовательности. В конечном итоге результатом является R-диаграмма, которую можно преобразовать обратно в более простое логическое выражение.

Например, возьмем следующее выражение:

${\displaystyle (Q\leftrightarrow P)\lor (\lnot P\land Q)\,}$

Это можно упростить с помощью R-диаграмм следующим образом:

${\displaystyle (}$${\displaystyle \leftrightarrow}$${\displaystyle )\lor (}$${\displaystyle \земля}$${\displaystyle )}$

${\displaystyle \лор }$

что равно:

${\displaystyle P\rightarrow Q.\,}$

Аналогично, R-диаграммы могут использоваться для доказательства или опровержения логических аргументов. Возьмем, к примеру, известный аргумент modus ponens , также известный как устранение импликации:

${\displaystyle {\frac {P\to Q,P}{\therefore Q}}}$

Это можно преобразовать в тавтологическое логическое выражение,

${\displaystyle ((P\to Q)\land P)\to Q}$

которые затем можно упростить с помощью R-диаграмм:

${\displaystyle ((}$${\displaystyle \to }$${\displaystyle )\land }$${\displaystyle )\to }$

${\displaystyle (}$${\displaystyle \land }$${\displaystyle )\to }$

${\displaystyle \to }$

Результатом является R-диаграмма, в которой каждый пробел имеет точку. Это означает, что аргумент является тавтологией; он верен во всех случаях. R-диаграмма, в которой ни один пробел не имеет точки, является противоречием , утверждением, которое никогда не является истинным.

R-диаграммы также используются в теории множеств как альтернатива диаграммам Венна. В теории множеств каждая линия представляет множество вместо логического утверждения; A заменяет p, а B заменяет q. При использовании для множеств точка над линией представляет включение, а точка под ней представляет исключение. Как и в логике, основные операции с множествами можно представить визуально с помощью R-диаграмм:

Базовые операции с множествами

Имя	Обозначение	R-диаграмма
Союз	${\displaystyle A\cup B}$
Пересечение	${\displaystyle A\cap B}$
Абсолютное дополнение	${\displaystyle A^{c}}$
Относительное дополнение (разность множеств)	${\displaystyle A\smallsetminus B}$
Симметричная разница	${\displaystyle A\Delta B}$

R-диаграммы иллюстрируют эквивалентность между теоретико-множественными и логическими понятиями: пересечение в теории множеств эквивалентно конъюнкции в логике, а объединение в теории множеств эквивалентно логической дизъюнкции.