Квикхалл

Quickhull — это метод вычисления выпуклой оболочки конечного множества точек в n -мерном пространстве. Он использует подход «разделяй и властвуй», аналогичный подходу быстрой сортировки , от которой и произошло его название. Его наихудшая временная сложность для 2-мерного и 3-мерного пространства составляет , но когда точность ввода ограничена битами, его наихудшая временная сложность предположительно составляет , где — число входных точек, а — число обработанных точек (до ). ^[1]${\displaystyle O(n^{2})}$${\displaystyle O(\log n)}$${\displaystyle O(n\log r)}$${\displaystyle n}$${\displaystyle r}$${\displaystyle n}$

N-мерный Quickhull был изобретен в 1996 году К. Брэдфордом Барбером, Дэвидом П. Добкиным и Ханну Хухданпаа. ^[1] Он был расширением планарного алгоритма Quickhull Джонатана Скотта Гринфилда 1990 года, хотя авторы 1996 года не знали о его методах. ^[2] Вместо этого Барбер и др. описывают его как детерминированный вариант алгоритма Кларксона и Шора 1989 года. ^[1]

Двумерный алгоритм можно разбить на следующие шаги: ^[2]

1. Найдите точки с минимальными и максимальными координатами x, поскольку они всегда будут частью выпуклой оболочки. Если существует много точек с одинаковыми минимальными/максимальными x, используйте те, у которых соответственно минимальные/максимальные y.
2. Используйте линию, образованную двумя точками, чтобы разделить множество на два подмножества точек, которые будут обработаны рекурсивно. Далее мы опишем, как определить часть корпуса над линией; часть корпуса под линией может быть определена аналогично.
3. Определите точку над прямой, максимально удаленную от прямой. Эта точка образует треугольник с двумя точками на прямой.
4. Точки, лежащие внутри этого треугольника, не могут быть частью выпуклой оболочки и поэтому могут быть проигнорированы на следующих этапах.
5. Рекурсивно повторите предыдущие два шага на двух линиях, образованных двумя новыми сторонами треугольника.
6. Продолжайте до тех пор, пока не останется ни одной точки, рекурсия не завершится и выбранные точки не составят выпуклую оболочку.

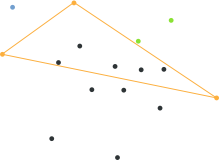
Проблема более сложна в случае более высокой размерности, поскольку оболочка состоит из многих граней; структура данных должна учитывать это и записывать линию/плоскость/гиперплоскость (хребет), общие для соседних граней. Для d измерений: ^[1]

1. Выбираем d + 1 точек из набора, которые не разделяют плоскость или гиперплоскость. Это формирует начальную оболочку с гранями Fs[] .
2. Для каждого F в Fs[] найти все неназначенные точки, которые находятся «выше» него; т. е. направлены от центра оболочки, и назначить их «внешнему» набору FO, связанному с F. Алгоритм сохраняет инвариант, что каждая точка, которая не была добавлена ​​к оболочке, но потенциально может быть ее вершиной, назначается ровно одному внешнему набору.
3. Для каждого F с непустым FO :
   1. Найдите точку p в FO с максимальным расстоянием от F и добавьте ее к оболочке. Обратите внимание, что p не обязательно будет вершиной окончательной оболочки, так как она может быть удалена позже.
   2. Создайте видимый набор V и инициализируйте его F. Расширьте V во всех направлениях для соседних граней Fv до тех пор, пока из p не перестанут быть видны другие грани . Видимость Fv из p означает, что p находится выше Fv.
   3. Граница V тогда образует множество хребтов горизонта H.
   4. Пусть Fnew[] будет набором граней, созданных из p и всех гребней в H.
   5. Отменить назначение всех точек во внешних наборах граней в V. Для каждой новой грани в Fnew[] выполните шаг (2), рассматривая только эти новые неназначенные точки для инициализации ее внешнего набора. Обратите внимание, что каждая точка, которая остается неназначенной в конце этого процесса, лежит внутри текущей оболочки.
   6. Удалим теперь внутренние грани в V из Fs[] . Добавьте новые грани в Fnew[] в Fs[] и продолжите итерацию.

Вход = набор S из n точекПредположим, что во входном наборе точек S имеется не менее 2 точек.функция QuickHull( S ) is  // Найти выпуклую оболочку из множества S из n точек Выпуклая оболочка := {} Найти самые левые и самые правые точки, скажем, A и B, и добавить A и B к выпуклой оболочке. Отрезок AB делит оставшиеся ( n − 2) точек на 2 группы S1 и S2 , где S1 — это точки в S, которые находятся справа от ориентированной прямой от A до B , и S2 — точки в S , которые находятся справа от ориентированной линии из B в A FindHull( S1 , A , B ) FindHull( S2 , B , A ) Вывод := Выпуклая оболочкаконечная функцияФункция FindHull( Sk , P , Q ) //  Находит точки на выпуклой оболочке из множества точек Sk  , // которые находятся на правой стороне ориентированной прямой от P до Q,  если  Sk не имеет точек , то  возвращается Из заданного множества точек в Sk находим самую дальнюю точку, скажем C , от отрезка PQ Добавляем точку C к выпуклой оболочке в месте между P и Q Три точки P , Q и C разбивают оставшиеся точки Sk на 3 подмножества: S0 , S1 и S2 , где S0 — точки внутри треугольника PCQ, S1 — точки на правой стороне ориентированной линия от P до C , а S2 — точки на правой стороне ориентированной линии от C до Q. FindHull( S1 , P , C ) FindHull( S2 , C , Q ) конечная функция

Псевдокод, специализированный для 3D-случая, доступен у Джордана Смита. Он включает в себя похожую стратегию «максимальной точки» для выбора стартовой оболочки. Если эти максимальные точки вырождены, то и все облако точек вырождено. ^[3]

• Алгоритмы выпуклой оболочки

• Дэйв Маунт. "Лекция 3: Еще больше алгоритмов выпуклой оболочки". Архивировано из оригинала 11 апреля 2001 г.

• Реализация QuickHull (GDC 2014) – презентация алгоритма с подробностями трехмерной реализации.