QR-алгоритм
Алгоритм расчета собственных значений

В числовой линейной алгебре алгоритм QR или итерация QR — это алгоритм собственных значений : то есть процедура вычисления собственных значений и собственных векторов матрицы . Алгоритм QR был разработан в конце 1950-х годов Джоном Г. Фрэнсисом и Верой Н. Кублановской , работавшими независимо друг от друга. [1] [2] [ 3] Основная идея заключается в выполнении разложения QR , записи матрицы в виде произведения ортогональной матрицы и верхней треугольной матрицы , умножении множителей в обратном порядке и итерации.

Практический QR-алгоритм

Формально, пусть A будет вещественной матрицей, собственные значения которой мы хотим вычислить, и пусть A 0  := A . На k -м шаге (начиная с k = 0 ) мы вычисляем QR-разложение A k = Q k  R k , где Q k - ортогональная матрица (т. е. Q T = Q −1 ), а R k - верхняя треугольная матрица. Затем мы формируем A k +1 = R k  Q k . Обратите внимание, что все A k подобны и , следовательно, имеют одинаковые собственные значения. Алгоритм численно устойчив, поскольку он выполняется с помощью ортогональных преобразований подобия. А к + 1 = Р к В к = В к − 1 В к Р к В к = В к − 1 А к В к = В к Т А к В к , {\displaystyle A_{k+1}=R_{k}Q_{k}=Q_{k}^{-1}Q_{k}R_{k}Q_{k}=Q_{k}^{-1} A_{k}Q_{k}=Q_{k}^{\mathsf {T}}A_{k}Q_{k},}

При определенных условиях [4] матрицы A k сходятся к треугольной матрице, форме Шура матрицы A . Собственные значения треугольной матрицы перечислены на диагонали, и проблема собственных значений решена. При проверке сходимости непрактично требовать точных нулей, [ требуется цитата ], но теорема Гершгорина о круге дает ограничение на ошибку.

В этой грубой форме итерации относительно дороги. Это можно смягчить, сначала приведя матрицу A к верхней форме Хессенберга (что требует арифметических операций с использованием техники, основанной на редукции Хаусхолдера ), с конечной последовательностью ортогональных преобразований подобия, что-то вроде двустороннего разложения QR. [5] [6] (Для разложения QR рефлекторы Хаусхолдера умножаются только слева, но для случая Хессенберга они умножаются как слева, так и справа.) Определение QR-разложения верхней матрицы Хессенберга требует арифметических операций. Более того, поскольку форма Хессенберга уже почти верхнетреугольная (она имеет только один ненулевой элемент под каждой диагональю), использование ее в качестве отправной точки сокращает количество шагов, необходимых для сходимости алгоритма QR. 10 3 н 3 + О ( н 2 ) {\textstyle {\tfrac {10}{3}}n^{3}+{\mathcal {O}}(n^{2})} 6 н 2 + О ( н ) {\textstyle 6n^{2}+{\mathcal {O}}(n)}

Если исходная матрица симметрична , то верхняя матрица Хессенберга также симметрична и, следовательно, трехдиагональна , и все A k тоже . Эта процедура требует арифметических операций с использованием метода, основанного на редукции Хаусхолдера. [5] [6] Определение QR-разложения симметричной трехдиагональной матрицы требует операций. [7] 4 3 н 3 + О ( н 2 ) {\textstyle {\tfrac {4}{3}}n^{3}+{\mathcal {O}}(n^{2})} О ( н ) {\displaystyle {\mathcal {O}}(n)}

Скорость сходимости зависит от разделения между собственными значениями, поэтому практический алгоритм будет использовать сдвиги, явные или неявные, для увеличения разделения и ускорения сходимости. Типичный симметричный алгоритм QR изолирует каждое собственное значение (затем уменьшает размер матрицы) всего за одну или две итерации, что делает его эффективным и надежным. [ требуется пояснение ]

Визуализация

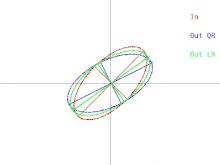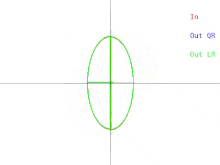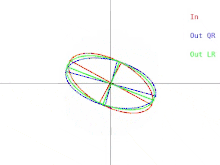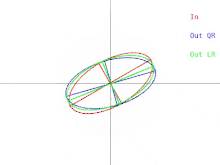
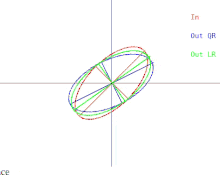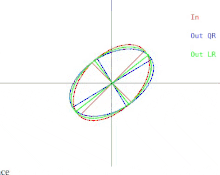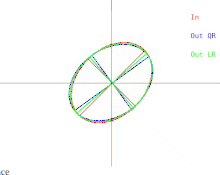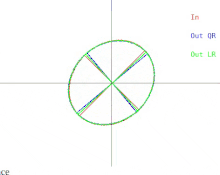
Рисунок 1: Как выходные данные одной итерации алгоритма QR или LR изменяются вместе с входными данными

Базовый алгоритм QR можно визуализировать в случае, когда A — положительно определенная симметричная матрица. В этом случае A можно изобразить как эллипс в 2 измерениях или эллипсоид в более высоких измерениях. Связь между входными данными алгоритма и одной итерацией можно изобразить, как на рисунке 1 (нажмите, чтобы увидеть анимацию). Обратите внимание, что алгоритм LR изображен рядом с алгоритмом QR.

Одна итерация заставляет эллипс наклоняться или «падать» по направлению к оси x. В случае, когда большая полуось эллипса параллельна оси x, одна итерация QR ничего не делает. Другая ситуация, когда алгоритм «ничего не делает», — это когда большая полуось параллельна оси y, а не оси x. В этом случае эллипс можно рассматривать как балансирующий ненадежно, не имея возможности упасть ни в одном направлении. В обеих ситуациях матрица диагональна. Ситуация, когда итерация алгоритма «ничего не делает», называется неподвижной точкой . Стратегия, используемая алгоритмом, — это итерация по направлению к неподвижной точке . Заметьте, что одна неподвижная точка устойчива, а другая неустойчива. Если бы эллипс был отклонен от нестабильной неподвижной точки на очень небольшую величину, одна итерация QR заставила бы эллипс наклониться от неподвижной точки, а не к ней. Однако в конечном итоге алгоритм сойдется к другой неподвижной точке, но это займет много времени.

Нахождение собственных значений и нахождение собственных векторов

Рисунок 2: Как влияет на результат одной итерации QR или LR, когда два собственных значения приближаются друг к другу

Стоит отметить, что нахождение даже одного собственного вектора симметричной матрицы невычислимо (в точной вещественной арифметике согласно определениям в вычислимом анализе ). [8] Эта трудность существует всякий раз, когда кратности собственных значений матрицы неизвестны. С другой стороны, такой же проблемы не существует для нахождения собственных значений. Собственные значения матрицы всегда вычислимы.

Теперь мы обсудим, как эти трудности проявляются в базовом алгоритме QR. Это показано на рисунке 2. Напомним, что эллипсы представляют собой положительно определенные симметричные матрицы. Когда два собственных значения входной матрицы приближаются друг к другу, входной эллипс превращается в круг. Круг соответствует кратному единичной матрицы. Почти круг соответствует почти кратному единичной матрицы, собственные значения которой почти равны диагональным элементам матрицы. Поэтому в этом случае задача приблизительного нахождения собственных значений оказывается простой. Но обратите внимание, что происходит с полуосями эллипсов. Итерация QR (или LR) наклоняет полуоси все меньше и меньше по мере того, как входной эллипс приближается к кругу. Собственные векторы могут быть известны только тогда, когда полуоси параллельны осям x и y. Число итераций, необходимых для достижения почти параллельности, неограниченно увеличивается по мере того, как входной эллипс становится более круглым.

Хотя вычислить собственное разложение произвольной симметричной матрицы может быть невозможно, всегда можно возмущение матрицы на произвольно малую величину и вычислить собственное разложение результирующей матрицы. В случае, когда матрица изображена как почти круг, матрицу можно заменить на ту, изображением которой является идеальный круг. В этом случае матрица является кратной единичной матрицы, и ее собственное разложение происходит немедленно. Однако следует помнить, что полученный собственный базис может быть довольно далек от исходного собственного базиса.

Ускорение: смещение и сдувание

Замедление, когда эллипс становится более круглым, имеет обратную сторону: оказывается, что когда эллипс становится более растянутым - и менее круглым - то вращение эллипса становится быстрее. Такое растяжение может быть вызвано, когда матрица , которую представляет эллипс, заменяется на , где приблизительно является наименьшим собственным значением . В этом случае отношение двух полуосей эллипса приближается к . В более высоких измерениях сдвиг, подобный этому, делает длину наименьшей полуоси эллипсоида малой относительно других полуосей, что ускоряет сходимость к наименьшему собственному значению, но не ускоряет сходимость к другим собственным значениям. Это становится бесполезным, когда наименьшее собственное значение полностью определено, поэтому матрицу затем необходимо дефляционировать , что просто означает удаление ее последней строки и столбца. М {\displaystyle М} М − λ я {\displaystyle M-\лямбда I} λ {\displaystyle \лямбда} М {\displaystyle М} ∞ {\displaystyle \infty}

Проблема с нестабильной неподвижной точкой также должна быть решена. Эвристика сдвига часто предназначена для решения этой проблемы: Практические сдвиги часто являются прерывистыми и рандомизированными. Сдвиг Уилкинсона, который хорошо подходит для симметричных матриц, таких как те, которые мы визуализируем, в частности, является прерывистым.

Неявный алгоритм QR

В современной вычислительной практике алгоритм QR выполняется в неявной версии, что упрощает введение использования множественных сдвигов. [4] Сначала матрица приводится к верхней форме Хессенберга , как в явной версии; затем на каждом шаге первый столбец преобразуется с помощью преобразования подобия Хаусхолдера малого размера в первый столбец [ необходимо разъяснение ] (или ), где , степени , является полиномом, определяющим стратегию сдвига (часто , где и являются двумя собственными значениями конечной главной подматрицы , так называемый неявный двойной сдвиг ). Затем выполняются последовательные преобразования Хаусхолдера размера для того, чтобы вернуть рабочую матрицу к верхней форме Хессенберга. Эта операция известна как погоня за выпуклостью , из-за особой формы ненулевых элементов матрицы вдоль шагов алгоритма. Как и в первой версии, дефляция выполняется, как только один из поддиагональных элементов становится достаточно малым. А 0 = В А В Т {\displaystyle A_{0}=QAQ^{\mathsf {T}}} А к {\displaystyle A_{k}} п ( А к ) {\displaystyle p(A_{k})} п ( А к ) е 1 {\displaystyle p(A_{k})e_{1}} п ( А к ) {\displaystyle p(A_{k})} г {\displaystyle r} п ( х ) = ( х − λ ) ( х − λ ¯ ) {\displaystyle p(x)=(x-\lambda )(x-{\bar {\lambda }})} λ {\displaystyle \лямбда} λ ¯ {\displaystyle {\bar {\lambda }}} 2 × 2 {\displaystyle 2\times 2} А к {\displaystyle A_{k}} г + 1 {\displaystyle r+1} А к {\displaystyle A_{k}} А к {\displaystyle A_{k}}

Предложение о переименовании

Поскольку в современной неявной версии процедуры QR-разложения явно не выполняются, некоторые авторы, например Уоткинс [9], предложили изменить его название на алгоритм Фрэнсиса . Голуб и Ван Лоан используют термин Francis QR step .

Интерпретация и конвергенция

Алгоритм QR можно рассматривать как более сложную вариацию базового алгоритма собственных значений "степени" . Напомним, что алгоритм степени многократно умножает A на один вектор, нормализуя после каждой итерации. Вектор сходится к собственному вектору наибольшего собственного значения. Вместо этого алгоритм QR работает с полным базисом векторов, используя разложение QR для повторной нормализации (и ортогонализации). Для симметричной матрицы A при сходимости AQ = QΛ , где Λ — диагональная матрица собственных значений, к которой сходится A , и где Q — это композиция всех ортогональных преобразований подобия, необходимых для этого. Таким образом, столбцы Q являются собственными векторами.

История

Алгоритму QR предшествовал алгоритм LR , который использует LU-разложение вместо QR-разложения. Алгоритм QR более стабилен, поэтому в настоящее время алгоритм LR используется редко. Однако он представляет собой важный шаг в развитии алгоритма QR.

Алгоритм LR был разработан в начале 1950-х годов Хайнцем Рутисхаузером , который в то время работал научным сотрудником Эдуарда Штифеля в ETH Zurich . Штифель предложил Рутисхаузеру использовать последовательность моментов y 0 T A k x 0 , k = 0, 1, ... (где x 0 и y 0 — произвольные векторы) для нахождения собственных значений A . Рутисхаузер взял алгоритм Александра Эйткена для этой задачи и развил его в алгоритм фактор-разности или алгоритм qd . После организации вычислений в подходящей форме он обнаружил, что алгоритм qd на самом деле является итерацией A k = L k U k (LU-разложение), A k +1 = U k L k , примененной к трехдиагональной матрице, из которой следует алгоритм LR. [10]

Другие варианты

Один из вариантов алгоритма QR , алгоритм Голуба-Кахана-Райнша, начинается с приведения общей матрицы к двухдиагональной. [11] Этот вариант алгоритма QR для вычисления сингулярных значений был впервые описан Голубом и Каханом (1965). Подпрограмма LAPACK DBDSQR реализует этот итерационный метод с некоторыми изменениями для покрытия случая, когда сингулярные значения очень малы (Demmel & Kahan 1990). Вместе с первым шагом, использующим отражения Хаусхолдера и, при необходимости, разложение QR , это формирует процедуру DGESVD для вычисления разложения сингулярных значений . Алгоритм QR также может быть реализован в бесконечных измерениях с соответствующими результатами сходимости. [12] [13]

Ссылки

  1. ^ JGF Francis, «Преобразование QR, I», The Computer Journal , 4 (3), страницы 265–271 (1961, получено в октябре 1959). doi:10.1093/comjnl/4.3.265
  2. ^ Фрэнсис, JGF (1962). «Преобразование QR, II». The Computer Journal . 4 (4): 332–345. doi : 10.1093/comjnl/4.4.332 .
  3. ↑ Вера Н. Кублановская, "О некоторых алгоритмах решения полной проблемы собственных значений", Журнал вычислительной математики и математической физики СССР , т. 1, № 3, стр. 637–657 (1963, получено в феврале 1961). Также опубликовано в: Журнал вычислительной математики и математической физики , т. 1, № 4, стр. 555–570 (1961). doi:10.1016/0041-5553(63)90168-X
  4. ^ ab Голуб, GH; Ван Лоан, CF (1996). Матричные вычисления (3-е изд.). Балтимор: Johns Hopkins University Press. ISBN 0-8018-5414-8.
  5. ^ ab Demmel, James W. (1997). Прикладная численная линейная алгебра . SIAM.
  6. ^ ab Трефетен, Ллойд Н .; Бау, Дэвид (1997). Численная линейная алгебра . SIAM.
  7. ^ Ортега, Джеймс М.; Кайзер, Генри Ф. (1963). «Методы LLT и QR для симметричных трехдиагональных матриц». The Computer Journal . 6 (1): 99–101. doi : 10.1093/comjnl/6.1.99 .
  8. ^ "линейная алгебра - Почему невычислимость спектрального разложения не является проблемой?". MathOverflow . Получено 2021-08-09 .
  9. ^ Уоткинс, Дэвид С. (2007). Задача о собственных значениях матрицы: методы ОТО и подпространства Крылова . Филадельфия, Пенсильвания: SIAM. ISBN 978-0-89871-641-2.
  10. ^ Парлетт, Бересфорд Н.; Гуткнехт, Мартин Х. (2011), «От qd к LR, или как были открыты алгоритмы qd и LR?» (PDF) , IMA Journal of Numerical Analysis , 31 (3): 741–754, doi :10.1093/imanum/drq003, hdl :20.500.11850/159536, ISSN  0272-4979
  11. ^ Бочканов Сергей Анатольевич. Руководство пользователя ALGLIB - Общие операции с матрицами - Сингулярное разложение. Проект ALGLIB. 2010-12-11. URL:[1] Дата обращения: 2010-12-11. (Архивировано WebCite по адресу https://www.webcitation.org/5utO4iSnR?url=http://www.alglib.net/matrixops/general/svd.php
  12. ^ Дейфт, Перси; Ли, Луенчау К.; Томей, Карлос (1985). «Потоки Тоды с бесконечным числом переменных». Журнал функционального анализа . 64 (3): 358–402. doi : 10.1016/0022-1236(85)90065-5 .
  13. ^ Колбрук, Мэтью Дж.; Хансен, Андерс К. (2019). «О бесконечномерном QR-алгоритме». Числовая математика . 143 (1): 17–83. arXiv : 2011.08172 . дои : 10.1007/s00211-019-01047-5 .

Источники

  • Деммель, Джеймс ; Кахан, Уильям (1990). «Точные сингулярные значения двухдиагональных матриц». Журнал SIAM по научным и статистическим вычислениям . 11 (5): 873–912. CiteSeerX  10.1.1.48.3740 . doi :10.1137/0911052.
  • Голуб, Джин Х.; Кахан , Уильям (1965). «Вычисление сингулярных значений и псевдообратной матрицы». Журнал Общества промышленной и прикладной математики, Серия B: Численный анализ . 2 (2): 205–224. Bibcode : 1965SJNA....2..205G. doi : 10.1137/0702016. JSTOR  2949777.
  • Задача на собственные значения на PlanetMath .
  • Заметки об ортогональных базисах и работе QR-алгоритма Питера Дж. Олвера
  • Модуль для QR-метода
  • Библиотека С++
Взято с "https://en.wikipedia.org/w/index.php?title=QR_algorithm&oldid=1247126137"