Алгоритм максимального потока Push-Relabel

В математической оптимизации алгоритм push–relabel (альтернативно, preflow–push algorithm ) — это алгоритм для вычисления максимальных потоков в потоковой сети . Название «push–relabel» происходит от двух основных операций, используемых в алгоритме. На протяжении всего выполнения алгоритм поддерживает «предпоток» и постепенно преобразует его в максимальный поток, перемещая поток локально между соседними узлами с помощью операций push под руководством допустимой сети, поддерживаемой операциями relabel . Для сравнения, алгоритм Форда–Фалкерсона выполняет глобальные дополнения, которые отправляют поток по путям от источника до стока. ^[1]

Алгоритм push-relabel считается одним из самых эффективных алгоритмов максимального потока. Общий алгоритм имеет сильно полиномиальную временную сложность O ( V  ² E ) , которая асимптотически более эффективна, чем алгоритм Эдмондса–Карпа O ( VE  ² ) . ^[2] Конкретные варианты алгоритмов достигают еще более низкой временной сложности. Вариант, основанный на правиле выбора узла с наивысшей меткой, имеет временную сложность O ( V  ² √ E ) и обычно рассматривается как эталон для алгоритмов максимального потока. ^{[3] [4]} Субкубическая временная сложность O ( VE log( V  ² / E )) может быть достигнута с помощью динамических деревьев , ^[2] хотя на практике это менее эффективно. ^{[ необходима цитата ]}

Алгоритм push-relabel был расширен для вычисления потоков с минимальной стоимостью . ^[5] Идея меток расстояний привела к более эффективному алгоритму увеличивающегося пути, который, в свою очередь, может быть включен обратно в алгоритм push-relabel для создания варианта с еще более высокой эмпирической производительностью. ^{[4] [6]}

Концепция предпотока была первоначально разработана Александром В. Карзановым и опубликована в 1974 году в «Советских математических докладах» 15. Этот алгоритм предпотока также использовал операцию проталкивания; однако он использовал расстояния во вспомогательной сети для определения того, куда проталкивать поток, вместо системы маркировки. ^{[2] [7]}

Алгоритм push-relabel был разработан Эндрю В. Голдбергом и Робертом Тарьяном . Алгоритм был первоначально представлен в ноябре 1986 года в STOC '86: Proceedings of the eighteenth annual ACM symposium on Theory of computing, а затем официально в октябре 1988 года в качестве статьи в Journal of the ACM. Обе статьи подробно описывают общую форму алгоритма, завершающуюся за O ( V  ² E ), вместе с последовательной реализацией O ( V  ³ ) , реализацией O ( VE  log( V  ² / E )) с использованием динамических деревьев и параллельной/распределенной реализацией. ^{[2] [8]} Как поясняется в ^[9] , Голдберг-Тарьян ввел метки расстояний, включив их в параллельный алгоритм максимального потока Йосси Шилоаха и Узи Вишкина . ^[10]

Позволять:

• G = ( V , E ) — сеть с функцией пропускной способности c : V × V → _∞${\displaystyle \mathbb {R} }$ ,
• F = ( G , c , s , t ) — сеть потоков , где s ∈ V и t ∈ V — выбранные вершины источника и стока соответственно,
• f  : V × V →${\displaystyle \mathbb {R} }$ обозначает предпоток в F ,
• x _f  : V →${\displaystyle \mathbb {R} }$ обозначим избыточную функцию относительно потока f , определяемую как x _f ( u ) = Σ _{v ∈ V} f ( v , u ) − Σ _{v ∈ V} f ( u , v ) ,
• c _f  : V × V → _∞${\displaystyle \mathbb {R} }$ обозначает функцию остаточной пропускной способности относительно потока f , определяемую как c _f  ( e ) = c ( e ) − f  ( e ) ,
• E _f ⊂ E — ребра, где f < c ,

и

• G _f ( V , E _f  ) обозначаютостаточную сеть Gотносительно потока f .

Алгоритм push–relabel использует неотрицательную целочисленную допустимую функцию маркировки , которая использует метки расстояний или высоты на узлах для определения того, какие дуги следует выбрать для операции push. Эта функция маркировки обозначается как 𝓁 : V →${\displaystyle \mathbb {N} }$ . Эта функция должна удовлетворять следующим условиям, чтобы считаться допустимой:

Действительная маркировка :

𝓁( u ) ≤ 𝓁( v ) + 1 для всех ( u , v ) ∈ E _f

Исходное состояние :

𝓁( s ) = |  V  |

Сохранение раковины :

𝓁( т ) = 0

В алгоритме значения меток s и t фиксированы. 𝓁( u ) — нижняя граница невзвешенного расстояния от u до t в G _{f ,}   если t достижим из u . Если u был отключен от t , то 𝓁( u ) − |  V  | — нижняя граница невзвешенного расстояния от u до s . В результате, если существует допустимая функция маркировки, в G _f нет путей s - t ,   поскольку ни один из таких путей не может быть длиннее |  V  | − 1 .

Дуга ( u , v ) ∈ E _f   называется допустимой, если 𝓁( u ) = 𝓁( v ) + 1 . Допустимая сеть G̃ _f ( V , Ẽ _f  ) состоит из множества дуг e ∈ E _f   , которые являются допустимыми. Допустимая сеть ациклична.

Для фиксированного потока f вершина v ∉ { s, t } называется активной , если она имеет положительный избыток относительно f , т. е. x _f ( u ) > 0 .

Алгоритм начинается с создания остаточного графа, инициализации значений предпотока нулем и выполнения набора насыщающих операций push на остаточных дугах ( s , v ), выходящих из источника, где v ∈ V \ { s } . Аналогично метки инициализируются таким образом, что метка в источнике представляет собой количество узлов в графе, 𝓁( s ) = |  V  | , а всем остальным узлам присваивается метка, равная нулю. После завершения инициализации алгоритм многократно выполняет операции push или relabel в отношении активных узлов до тех пор, пока не будет выполнена ни одна применимая операция.

Операция push применяется к допустимой внешней дуге ( u , v ) активного узла u в G _f . Она перемещает min{ x _f ( u ), c _​​f ( u , v )} единиц потока из u в v .

нажимаем (u, v): утверждать x f [u] > 0 и 𝓁[u] == 𝓁[v] + 1 Δ = min(x f [u], c[u][v] - f[u][v]) ф[у][в] += Δ f[v][u] -= Δ х ф [и] -= Δ х ф [в] += Δ

Операция push, которая заставляет f  ( u , v ) достичь c ( u , v ) , называется насыщающим push , поскольку она использует всю доступную емкость остаточной дуги. В противном случае весь избыток в узле проталкивается через остаточную дугу. Это называется ненасыщающим push или ненасыщающим push .

Операция перемаркировки применяется к активному узлу u, который не является ни источником, ни стоком без каких-либо допустимых исходящих дуг в G _f . Она изменяет 𝓁( u ) на минимальное значение, при котором создается допустимая исходящая дуга. Обратите внимание, что это всегда увеличивает 𝓁( u ) и никогда не создает крутую дугу, которая является дугой ( u , v ) такой, что c _f  ( u , v ) > 0 , и 𝓁( u ) > 𝓁( v ) + 1 .

переименовать(u): утверждают x f [u] > 0 и 𝓁[u] <= 𝓁[v] для всех v таких, что c f [u][v] > 0 𝓁[u] = 1 + min(𝓁[v] для всех v таких, что c f [u][v] > 0)

После операции push или перемаркировки 𝓁 остается допустимой функцией маркировки по отношению к f .

Для операции push на допустимой дуге ( u , v ) она может добавить дугу ( v , u ) к E _f , где 𝓁( v ) = 𝓁( u ) − 1 ≤ 𝓁( u ) + 1 ; она также может удалить дугу ( u , v ) из E _f , где она эффективно снимает ограничение 𝓁( u ) ≤ 𝓁( v ) + 1 .

Чтобы увидеть, что операция перемаркировки на узле u сохраняет действительность 𝓁( u ) , обратите внимание, что это тривиально гарантируется определением для исходящих дуг u в G _f . Для входящих дуг u в G _f увеличившееся 𝓁( u ) может только менее строго удовлетворять ограничениям, но не нарушать их.

Алгоритм generic push–relabel используется только в качестве доказательства концепции и не содержит подробностей реализации о том, как выбрать активный узел для операций push и relabel. Эта общая версия алгоритма завершится за O ( V ² E ) .

Так как 𝓁( s ) = |  V  | , 𝓁( t ) = 0 , и нет путей длиннее |  V  | − 1 в G _f , для того, чтобы 𝓁( s ) удовлетворял допустимому условию маркировки , s должен быть отключен от t . При инициализации алгоритм выполняет это требование, создавая предварительный поток f , который насыщает все исходящие дуги s , после чего 𝓁( v ) = 0 тривиально допустимо для всех v ∈ V \ { s , t } . После инициализации алгоритм многократно выполняет применимую операцию push или relabel до тех пор, пока такие операции не будут применены, после чего предварительный поток преобразуется в максимальный поток.

generic-push-relabel(G, c, s, t): создать предварительный поток f, который насыщает все исходящие дуги s пусть 𝓁[s] = |V| пусть 𝓁[v] = 0 для всех v ∈ V \ {s}, пока есть применимая операция push или relabel do выполнить операцию

Алгоритм поддерживает условие, что 𝓁 является допустимой маркировкой во время его выполнения. Это можно доказать, изучив эффекты операций push и relabel на функцию метки 𝓁 . Операция relabel увеличивает значение метки на соответствующий минимум плюс один, который всегда будет удовлетворять ограничению 𝓁( u ) ≤ 𝓁( v ) + 1. Операция push может отправить поток из u в v, если 𝓁( u ) = 𝓁( v ) + 1 . Это может добавить ( v , u ) к G _f  и может удалить ( u , v ) из G _f  . Добавление ( v , u ) к G _f  не повлияет на допустимую маркировку, поскольку 𝓁( v ) = 𝓁( u ) − 1 . Удаление ( u , v ) из Gf  удаляет соответствующее ограничение, поскольку допустимое свойство маркировки 𝓁 ₍ u ) ≤ 𝓁( v ) + 1 применяется только к остаточным дугам в Gf _.  ^[8]

Если существует предпоток f и допустимая маркировка 𝓁 для f , то в остаточном графе G _f нет увеличивающего пути от s до t . Это можно доказать от противного на основе неравенств, которые возникают в функции маркировки при предположении, что увеличивающий путь существует. Если алгоритм завершается, то все узлы в V \ { s , t } неактивны. Это означает, что все v ∈ V \ { s , t } не имеют избыточного потока, и без избытка предпоток f подчиняется ограничению сохранения потока и может считаться нормальным потоком. Этот поток является максимальным потоком согласно теореме о максимальном потоке и минимальном разрезе , поскольку нет увеличивающего пути от s до t . ^[8] 

Таким образом, по завершении работы алгоритм вернет максимальный поток.

Чтобы ограничить временную сложность алгоритма, мы должны проанализировать количество операций push и relabel, которые происходят в основном цикле. Количество операций relabel, saturating push и nonsaturating push анализируется отдельно.

В алгоритме операция перемаркировки может быть выполнена не более (2|  V  | − 1)(|  V  | − 2) < 2|  V  | ² раз. Это связано с тем, что значение маркировки 𝓁( u ) для любого узла u никогда не может уменьшиться, а максимальное значение метки не более 2|  V  | − 1 для всех узлов. Это означает, что операция перемаркировки потенциально может быть выполнена 2|  V  | − 1 раз для всех узлов V \ { s , t } (т. е. |  V  | − 2 ). Это приводит к ограничению O ( V  ² ) для операции перемаркировки.

Каждый насыщающий push на допустимой дуге ( u , v ) удаляет дугу из G _f  . Чтобы дуга была повторно вставлена ​​в G _f  для другого насыщающего push, v сначала должна быть перемаркирована, затем push на дуге ( v , u ) , затем u должна быть перемаркирована. В процессе 𝓁( u ) увеличивается как минимум на два. Следовательно, существует O ( V ) насыщающих push на ( u , v ) , а общее количество насыщающих push не превышает 2|  V  ||  E  | . Это приводит к временному ограничению O ( VE ) для операций насыщающего push.

Ограничение числа ненасыщающих push может быть достигнуто с помощью потенциального аргумента . Мы используем потенциальную функцию Φ = Σ _{[ u ∈ V ∧ x f  ( u ) > 0]} 𝓁( u ) (т. е. Φ является суммой меток всех активных узлов). Очевидно, что Φ изначально равно 0 и остается неотрицательным на протяжении всего выполнения алгоритма. Как перемаркировка, так и насыщающие push могут увеличить Φ . Однако значение Φ должно быть равно 0 при завершении, поскольку в конце выполнения алгоритма не может остаться никаких активных узлов. Это означает, что в ходе выполнения алгоритма ненасыщающие push-операции должны составлять разницу между операциями relabel и saturating push, чтобы Φ завершилось со значением 0. Операция relabel может увеличить Φ не более чем на (2|  V  | − 1)(|  V  | − 2) . Насыщающий push на ( u , v ) активирует v , если он был неактивен до push, увеличивая Φ не более чем на 2|  V  | − 1 . Следовательно, общий вклад всех операций saturating push в Φ не более чем на (2|  V  | − 1)(2|  V  ||  E  |) . Ненасыщающий push на ( u , v ) всегда деактивирует u , но он также может активировать v, как в насыщающем push. В результате он уменьшает Φ по крайней мере на 𝓁( u ) − 𝓁( v ) = 1 . Поскольку перемаркировки и насыщающие push увеличивают Φ , общее количество ненасыщающих push должно составлять разницу (2|  V  | − 1)(|  V  | − 2) + (2|  V  | − 1)(2|  V  ||  E  |) ≤ 4|  V  | ² |  E  | . Это приводит к временному ограничению O ( V  ² E ) для ненасыщающих операций push.

В целом, алгоритм выполняет O ( V  ² ) перемаркировок, O ( VE ) насыщающих push-ов и O ( V  ² E ) ненасыщающих push-ов. Структуры данных могут быть спроектированы для выбора и выполнения соответствующей операции за время O (1) . Таким образом, временная сложность алгоритма составляет O ( V  ² E ) . ^{[1] [8]}

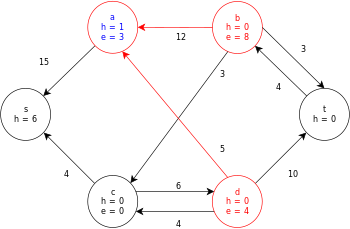
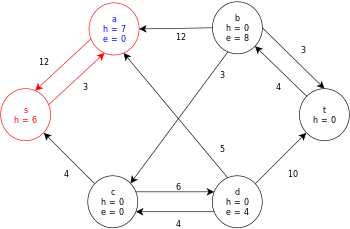
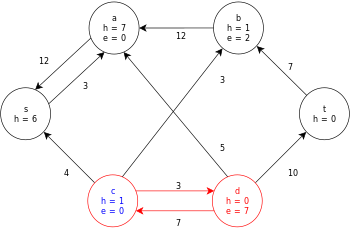
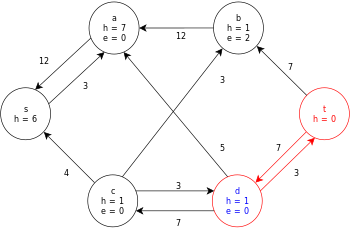
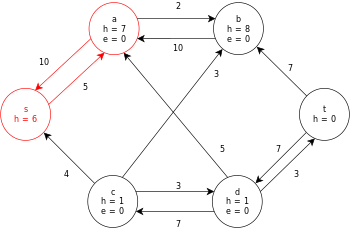
Ниже приведен пример выполнения универсального алгоритма push-relabel, определенного выше, на следующей простой схеме сетевого потока.

В примере значения h и e обозначают метку 𝓁 и избыток x _f  , соответственно, узла во время выполнения алгоритма. Каждый остаточный граф в примере содержит только остаточные дуги с емкостью больше нуля. Каждый остаточный граф может содержать несколько итераций цикла выполнения операции .

Операция(ы) алгоритма	Остаточный график
Инициализируйте остаточный график, установив предварительный поток на значения 0 и инициализировав маркировку.
Начальный насыщающий толчок выполняется по всем дугам предпотока из источника, s .
Узел a перемаркирован, чтобы направить его избыточный поток в сторону стока t . Избыток в точке a затем перемещается в точку b, а затем в точку d двумя последовательными насыщающими перемещениями; в результате чего в точке a все еще остается некоторый избыток.
И снова a перемаркируется, чтобы переместить его избыток вдоль его последнего оставшегося положительного остатка (т.е. переместить избыток обратно в s ). Затем узел a удаляется из набора активных узлов.
Переименуем b , а затем переместим его избыток в t и c .
Переименуйте c и переместите его избыток в d .
Переименуйте d и затем переместите его избыток в t .
В результате узел b остается единственным активным узлом, но он не может направить свой избыточный поток в сторону стока. Переименуем b , а затем протолкнем его избыток к источнику s через узел a .
Отодвиньте последний излишек назад к источнику, s . Активных узлов не осталось. Алгоритм завершается и возвращает максимальный поток графа (как показано выше).

Пример (но с начальным потоком 0) можно запустить здесь в интерактивном режиме.

В то время как общий алгоритм push–relabel имеет временную сложность O ( V  ² E ) , эффективные реализации достигают O ( V  ³ ) или более низкой временной сложности за счет применения соответствующих правил при выборе применимых операций push и relabel. Эмпирическая производительность может быть дополнительно улучшена с помощью эвристики.

Структура данных "current-arc" представляет собой механизм посещения входящих и исходящих соседей узла в потоковой сети в статическом кольцевом порядке. Если для узла создается односвязный список соседей, структура данных может быть такой же простой, как указатель на список, который проходит по списку и возвращается к началу, когда он заканчивается.

На основе структуры данных «текущая дуга» можно определить операцию разряда. Операция разряда применяется к активному узлу и многократно выталкивает поток из узла, пока он не станет неактивным, перемаркируя его по мере необходимости для создания допустимых дуг в процессе.

discharge(u): while x f [u] > 0 do  if current-arc[u] вышел за пределы neighbors[u] then переименовать(u) перемотка тока-дуги[u] иначе  пусть (u, v) = current-arc[u] если (u, v) допустимо , то нажимаем (u, v) пусть current-arc[u] указывает на следующего соседа u

Поиск следующего допустимого ребра для перемещения имеет амортизированную сложность . Указатель текущей дуги перемещается к следующему соседу только тогда, когда ребро к текущему соседу насыщено или недопустимо, и ни одно из этих двух свойств не может измениться, пока активный узел не будет перемаркирован. Таким образом, когда указатель уходит, допустимых ненасыщенных ребер нет, и нам приходится перемаркировать активный узел , поэтому перемещение указателя оплачивается операцией перемаркировки. ^[8]${\displaystyle O(1)}$ ${\displaystyle u}$${\displaystyle u}$${\displaystyle O(V)}$${\displaystyle O(V)}$

Определение операции разрядки сводит алгоритм push–relabel к многократному выбору активного узла для разрядки. В зависимости от правила выбора алгоритм демонстрирует различную временную сложность. Для краткости мы игнорируем s и t при ссылке на узлы в следующем обсуждении.

Алгоритм FIFO push–relabel ^[2] организует активные узлы в очередь. Начальные активные узлы могут быть вставлены в произвольном порядке. Алгоритм всегда удаляет узел в начале очереди для выгрузки. Всякий раз, когда неактивный узел становится активным, он добавляется в конец очереди.

Алгоритм имеет временную сложность O ( V  ³ ) .

Алгоритм relabel-to-front push–relabel ^[1] организует все узлы в связанный список и сохраняет инвариант, что список топологически отсортирован относительно допустимой сети. Алгоритм сканирует список от начала до конца и выполняет операцию разрядки на текущем узле, если он активен. Если узел перемаркирован, он перемещается в начало списка, и сканирование перезапускается с начала.

Алгоритм также имеет временную сложность O ( V  ³ ) .

Алгоритм push-relabel с наивысшей меткой ^[11] организует все узлы в сегменты, индексированные по их меткам. Алгоритм всегда выбирает активный узел с наибольшей меткой для выгрузки.

Алгоритм имеет временную сложность O ( V  ² √ E ) . Если вместо этого использовать правило выбора наименьшей метки, временная сложность становится O ( V  ² E ) . ^[3]

Хотя в описании общего алгоритма push-relabel выше 𝓁( u ) устанавливается равным нулю для каждого узла u, кроме s и t в начале, предпочтительнее выполнить обратный поиск в ширину от t для вычисления точных меток. ^[2]

Алгоритм обычно разделяется на две фазы. Фаза 1 вычисляет максимальный предварительный поток, выгружая только активные узлы, метки которых ниже n . Фаза 2 преобразует максимальный предварительный поток в максимальный поток, возвращая избыточный поток, который не может достичь t , в s . Можно показать, что фаза 2 имеет временную сложность O ( VE ) независимо от порядка операций push и relabel и, следовательно, доминирует над фазой 1. В качестве альтернативы, ее можно реализовать с помощью разложения потока. ^[9]

Эвристики имеют решающее значение для улучшения эмпирической производительности алгоритма. ^[12] Две наиболее часто используемые эвристики — это эвристика пробелов и эвристика глобальной перемаркировки. ^{[2] [13]} Эвристика пробелов обнаруживает пробелы в функции маркировки. Если есть метка 0 < 𝓁 ' < |  V  |, для которой нет узла u такого, что 𝓁( u ) = 𝓁 ' , то любой узел u с 𝓁 ' < 𝓁( u ) < |  V  | был отключен от t и может быть немедленно перемаркирован в (|  V  | + 1) . Эвристика глобальной перемаркировки периодически выполняет обратный поиск в ширину из t в G _f  для вычисления точных меток узлов. Обе эвристики пропускают бесполезные операции перемаркировки, которые являются узким местом алгоритма и способствуют неэффективности динамических деревьев. ^[4]

#include <stdlib.h> #include <stdio.h>  #define УЗЛЫ 6 #define MIN(X,Y) ((X) < (Y) ? (X) : (Y)) #define INFINITE 10000000void push ( const int * const * C , int ** F , int * избыток , int u , int v ) { int send = MIN ( избыток [ u ], C [ u ][ v ] - F [ u ][ v ]); F [ u ][ v ] += отправить ; F [ v ][ u ] -= отправить ; избыток [ u ] -= отправить ; избыток [ v ] += отправить ; }                                   void relabel ( const int * const * C , const int * const * F , int * height , int u ) { int v ; int min_height = INFINITE ; for ( v = 0 ; v < NODES ; v ++ ) { if ( C [ u ][ v ] - F [ u ][ v ] > 0 ) { min_height = MIN ( min_height , height [ v ]); height [ u ] = min_height + 1 ; } } } ;                                                  void discharge ( const int * const * C , int ** F , int * избыток , int * высота , int * видно , int u ) { while ( избыток [ u ] > 0 ) { if ( видно [ u ] < УЗЛЫ ) { int v = видно [ u ]; if (( C [ u ][ v ] - F [ u ][ v ] > 0 ) && ( высота [ u ] > высота [ v ])) { push ( C , F , избыток , u , v ); } else { видно [ u ] += 1 ; } } else { relabel ( C , F , высота , u ); видно [ u ] = 0 ; } } }                                                                   void moveToFront ( int i , int * A ) { int temp = A [ i ]; int n ; for ( n = i ; n > 0 ; n -- ) { A [ n ] = A [ n -1 ]; } A [ 0 ] = temp ; }                           int pushRelabel ( const int * const * C , int ** F , int source , int sink ) { int * избыток , * высота , * список , * увиденное , i , p ;                      избыток = ( int * ) calloc ( УЗЛЫ , sizeof ( int )); высота = ( int * ) calloc ( УЗЛЫ , sizeof ( int )); видно = ( int * ) calloc ( УЗЛЫ , sizeof ( int ));                  список = ( целое число * ) calloc (( УЗЛЫ -2 ), sizeof ( целое число ));      для ( i = 0 , p = 0 ; i < УЗЛЫ ; i ++ ) { если (( i != источник ) && ( i != приемник )) { список [ p ] = i ; p ++ ; } }                          высота [ источник ] = УЗЛЫ ; избыток [ источник ] = БЕСКОНЕЧНОСТЬ ; для ( i = 0 ; i < УЗЛЫ ; i ++ ) push ( C , F , избыток , источник , i );                   p = 0 ; while ( p < NODES - 2 ) { int u = list [ p ]; int old_height = height [ u ]; discharge ( C , F , extra , height , seen , u ); if ( height [ u ] > old_height ) { moveToFront ( p , list ); p = 0 ; } else { p += 1 ; } } int maxflow = 0 ; for ( i = 0 ; i < NODES ; i ++ ) maxflow += F [ source ][ i ];                                                         бесплатно ( список ); свободный ( видимый ); свободный ( высота ); свободный ( избыток );   вернуть максимальный поток ; } void printMatrix ( const int * const * M ) { int i , j ; for ( i = 0 ; i < УЗЛЫ ; i ++ ) { for ( j = 0 ; j < УЗЛЫ ; j ++ ) printf ( "%d \t " , M [ i ][ j ]); printf ( " \n " ); } }                              int main ( void ) { int ** flow , ** capacitys , i ; flow = ( int ** ) calloc ( NODES , sizeof ( int * )); capacity = ( int ** ) calloc ( NODES , sizeof ( int * )); for ( i = 0 ; i < NODES ; i ++ ) { flow [ i ] = ( int * ) calloc ( NODES , sizeof ( int )); capacity [ i ] = ( int * ) calloc ( NODES , sizeof ( int )); }                                         // Пример графа мощности [ 0 ][ 1 ] = 2 ; мощности [ 0 ][ 2 ] = 9 ; мощности [ 1 ][ 2 ] = 1 ; мощности [ 1 ][ 3 ] = 0 ; мощности [ 1 ][ 4 ] = 0 ; мощности [ 2 ][ 4 ] = 7 ; мощности [ 3 ][ 5 ] = 7 ; мощности [ 4 ][ 5 ] = 4 ;                         printf ( "Вместимость: \n " ); printMatrix ( емкости );  printf ( "Максимальный поток: \n %d \n " , pushRelabel ( емкости , поток , 0 , 5 ));     printf ( "Потоки: \n " ); printMatrix ( flow );  вернуть 0 ; } 

def  relabel_to_front ( C ,  source :  int ,  sink :  int )  ->  int :  n  =  len ( C )  # C - матрица пропускной способности  F  =  [[ 0 ]  *  n  for  _  in  range ( n )]  # остаточная пропускная способность от u до v равна C[u][v] - F[u][v] height  =  [ 0 ]  *  n  # высота узла  избыток  =  [ 0 ]  *  n  # поток в узел минус поток из узла  виден  =  [ 0 ]  *  n  # соседи видны с момента последней перемаркировки  # узел "очередь"  nodelist  =  [ i  for  i  in  range ( n )  if  i  !=  source  and  i  !=  sink ] def  push ( u ,  v ):  send  =  min ( excess [ u ],  C [ u ][ v ]  -  F [ u ][ v ])  F [ u ][ v ]  +=  send  F [ v ][ u ]  -=  send  extra [ u ]  -=  send  extra [ v ]  +=  send def  relabel ( u ):  # Найти наименьшую новую высоту, делающую возможным толчок,  # если такой толчок вообще возможен.  min_height  =  ∞  для  v  в  диапазоне ( n ):  если  C [ u ][ v ]  -  F [ u ][ v ]  >  0 :  min_height  =  min ( min_height ,  height [ v ])  height [ u ]  =  min_height  +  1 def  discharge ( u ):  while  extra [ u ]  >  0 :  if  seen [ u ]  <  n :  # проверить следующего соседа  v  =  seen [ u ]  if  C [ u ][ v ]  -  F [ u ][ v ]  >  0  and  height [ u ]  >  height [ v ]:  push ( u ,  v )  else :  seen [ u ]  +=  1  else :  # мы проверили всех соседей. необходимо перемаркировать  relabel ( u )  seen [ u ]  =  0 height [ source ]  =  n  # самый длинный путь от источника до стока меньше n long  extra [ source ]  =  ∞  # отправить как можно больше потока соседям источника  for  v  in  range ( n ):  push ( source ,  v ) p  =  0  while  p  <  len ( nodelist ):  u  =  nodelist [ p ]  old_height  =  height [ u ]  discharge ( u )  if  height [ u ]  >  old_height :  nodelist . insert ( 0 ,  nodelist . pop ( p ))  # перейти в начало списка  p  =  0  # начать с начала списка  else :  p  +=  1 возврат  суммы ( F [ источник ])