Псевдовыпуклая функция

В выпуклом анализе и вариационном исчислении , обеих ветвях математики , псевдовыпуклая функция — это функция , которая ведет себя как выпуклая функция относительно нахождения своих локальных минимумов , но на самом деле не обязательно является выпуклой. Неформально, дифференцируемая функция является псевдовыпуклой, если она возрастает в любом направлении, где она имеет положительную производную по направлению . Свойство должно выполняться во всей области определения функции, а не только для близлежащих точек.

Формальное определение

Рассмотрим дифференцируемую функцию , определенную на (непустом) выпуклом открытом множестве конечномерного евклидова пространства . Эта функция называется псевдовыпуклой, если выполняется следующее свойство: [1] ф : Х ⊆ Р н → Р {\displaystyle f:X\subseteq \mathbb {R} ^{n}\rightarrow \mathbb {R} } Х {\displaystyle X} Р н {\displaystyle \mathbb {R} ^{n}}

для всех . х , у ∈ Х : ∇ ф ( х ) ⋅ ( у − х ) ≥ 0 ⇒ ф ( у ) ≥ ф ( х ) {\displaystyle x,y\in X:\quad \nabla f(x)\cdot (yx)\geq 0\Стрелка вправо f(y)\geq f(x)}

Эквивалентно:

для всех . х , у ∈ Х : ф ( у ) < ф ( х ) ⇒ ∇ ф ( х ) ⋅ ( у − х ) < 0 {\displaystyle x,y\in X:\quad f(y)<f(x)\Rightarrow \nabla f(x)\cdot (yx)<0}

Вот градиент , определяемый как : ∇ ф {\displaystyle \набла ф} ф {\displaystyle f} ∇ ф = ( ∂ ф ∂ х 1 , … , ∂ ф ∂ х н ) . {\displaystyle \nabla f=\left({\frac {\partial f}{\partial x_{1}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right).}

Обратите внимание, что определение может быть также выражено в терминах производной по направлению , в направлении, заданном вектором . Это происходит потому, что, поскольку является дифференцируемым, эта производная по направлению задается как: ф {\displaystyle f} в = у − х {\displaystyle v=yx} ф {\displaystyle f}

∂ ф ∂ в ( х ) = ∇ ф ( х ) ⋅ в = ∇ ф ( х ) ⋅ ( у − х ) . {\displaystyle {\frac {\partial f}{\partial v}}(x)=\nabla f(x)\cdot v=\nabla f(x)\cdot (yx).}

Характеристики

Отношение к другим типам «выпуклости»

Каждая выпуклая функция является псевдовыпуклой, но обратное неверно. Например, функция является псевдовыпуклой, но не выпуклой. Аналогично, любая псевдовыпуклая функция является квазивыпуклой ; но обратное неверно, поскольку функция является квазивыпуклой, но не псевдовыпуклой. Это можно схематически обобщить следующим образом: ф ( х ) = х + х 3 {\displaystyle f(x)=x+x^{3}} ф ( х ) = х 3 {\displaystyle f(x)=x^{3}}

выпуклый псевдовыпуклый квазивыпуклый ⇒ {\displaystyle \Стрелка вправо} ⇒ {\displaystyle \Стрелка вправо}
Функции x^3 (квазивыпуклая, но не псевдовыпуклая) и x^3 + x (псевдовыпуклая и, следовательно, квазивыпуклая). Ни одна из них не является выпуклой.
Функции x^3 (квазивыпуклая, но не псевдовыпуклая) и x^3 + x (псевдовыпуклая и, следовательно, квазивыпуклая). Ни одна из них не является выпуклой.

Чтобы увидеть, что не является псевдовыпуклым, рассмотрим его производную при : . Тогда, если бы был псевдовыпуклым, мы должны были бы иметь: ф ( х ) = х 3 {\displaystyle f(x)=x^{3}} х = 0 {\displaystyle x=0} ф ′ ( 0 ) = 0 {\displaystyle f^{\prime }(0)=0} ф ( х ) = х 3 {\displaystyle f(x)=x^{3}}

ф ′ ( 0 ) ( у − 0 ) = 0 ≥ 0 ⇒ ф ( у ) ≥ ф ( 0 ) , ∀ у ∈ Р . {\displaystyle f^{\prime }(0)(y-0)=0\geq 0\Rightarrow f(y)\geq f(0),\quad \forall \,y\in \mathbb {R} .}

В частности, это должно быть верно для . Но это не так, так как: . у = − 1 {\displaystyle у=-1} ф ( − 1 ) = ( − 1 ) 3 = − 1 < ф ( 0 ) = 0 {\displaystyle f(-1)=(-1)^{3}=-1<f(0)=0}

Достаточное условие оптимальности

Для любой дифференцируемой функции справедлива теорема Ферма , которая гласит: если имеет локальный минимум в точке в открытой области, то должна быть стационарной точкой ( то есть: ). ф {\displaystyle f} х ∗ {\displaystyle x^{*}} х ∗ {\displaystyle x^{*}} ф {\displaystyle f} ∇ ф ( х ∗ ) = 0 {\displaystyle \nabla f(x^{*})=0}

Псевдовыпуклость представляет большой интерес в области оптимизации , поскольку обратное также верно для любой псевдовыпуклой функции. То есть: [2] если является стационарной точкой псевдовыпуклой функции , то имеет глобальный минимум при . Отметим также, что результат гарантирует глобальный минимум (а не только локальный). х ∗ {\displaystyle x^{*}} ф {\displaystyle f} ф {\displaystyle f} х ∗ {\displaystyle x^{*}}

Этот последний результат также верен для выпуклой функции, но не верен для квазивыпуклой функции. Рассмотрим, например, квазивыпуклую функцию:

ф ( х ) = е х х 2 + 1 + 1 е х {\displaystyle f(x)={\frac {e^{x}}{x^{2}+1}}+{\frac {1}{e^{x}}}} .

Эта функция не псевдовыпуклая, а квазивыпуклая. Кроме того, точка является критической точкой , так как . Однако не имеет глобального минимума при (даже локального минимума). х = 0 {\displaystyle x=0} ф {\displaystyle f} ф ′ ( 0 ) = 0 {\displaystyle f^{\prime }(0)=0} ф {\displaystyle f} х = 0 {\displaystyle x=0}

Пример квазивыпуклой функции с критической точкой, не являющейся минимумом.
Пример квазивыпуклой функции, которая не является псевдовыпуклой. Функция имеет критическую точку при , но это не минимум. х = 0 {\displaystyle x=0}

Наконец, отметим, что псевдовыпуклая функция может не иметь критической точки. Возьмем, к примеру, псевдовыпуклую функцию: , производная которой всегда положительна: . ф ( х ) = х 3 + х {\displaystyle f(x)=x^{3}+x} ф ′ ( х ) = 3 х 2 + 1 > 0 , ∀ х ∈ Р {\displaystyle f^{\prime }(x)=3x^{2}+1>0,\,\forall \,x\in \mathbb {R} }

Примеры

Примером функции, которая является псевдовыпуклой, но не выпуклой, является: На рисунке показана эта функция для случая, когда . Этот пример можно обобщить на две переменные следующим образом: ф ( х ) = х 2 х 2 + к , к > 0. {\displaystyle f(x)={\frac {x^{2}}{x^{2}+k}},\,k>0.} к = 0.2 {\displaystyle к=0,2}

ф ( х ) = х 2 + у 2 х 2 + у 2 + к , к > 0. {\displaystyle f(x)={\frac {x^{2}+y^{2}}{x^{2}+y^{2}+k}},\,k>0.}
Псевдовыпуклая функция, которая не является выпуклой: x^2 / (x^2+0.2)
Псевдовыпуклая функция, которая не является выпуклой.

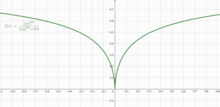
Предыдущий пример можно модифицировать, чтобы получить функцию, которая не является ни выпуклой, ни псевдовыпуклой, но является квазивыпуклой:

f ( x ) = | x | p | x | p + k , k > 0 , p ∈ ( 0 , 1 ) . {\displaystyle f(x)={\frac {|x|^{p}}{|x|^{p}+k}},\,k>0,\,p\in (0,1).}

На рисунке показана эта функция для случая, когда . Как видно, эта функция не является выпуклой из-за вогнутости, и она не является псевдовыпуклой, поскольку она не дифференцируема при . k = 0.5 , p = 0.6 {\displaystyle k=0.5,p=0.6} x = 0 {\displaystyle x=0}

Квазивыпуклая функция, которая не является ни выпуклой, ни псевдовыпуклой:
Квазивыпуклая функция, которая не является ни выпуклой, ни псевдовыпуклой.

Обобщение на недифференцируемые функции

Понятие псевдовыпуклости можно обобщить на недифференцируемые функции следующим образом. [3] Для любой функции мы можем определить верхнюю производную Дини следующим образом: f : X → R {\displaystyle f:X\rightarrow \mathbb {R} } f {\displaystyle f}

f + ( x , u ) = lim sup h → 0 + f ( x + h u ) − f ( x ) h ; {\displaystyle f^{+}(x,u)=\limsup _{h\to 0^{+}}{\frac {f(x+hu)-f(x)}{h}};}

где u — любой единичный вектор . Функция называется псевдовыпуклой, если она возрастает в любом направлении, где верхняя производная Дини положительна. Точнее, это характеризуется в терминах субдифференциала следующим образом: ∂ f {\displaystyle \partial f}

Для всех : если таково , что , то , для всех ; x , y ∈ X {\displaystyle x,y\in X} x ∗ ∈ ∂ f ( x ) {\displaystyle x^{*}\in \partial f(x)} ⟨ x ∗ , y − x ⟩ ≥ 0 {\displaystyle \langle x^{*},y-x\rangle \geq 0} f ( x ) ≤ f ( z ) {\displaystyle f(x)\leq f(z)} z ∈ [ x , y ] {\displaystyle z\in [x,y]}

где обозначает отрезок прямой, соединяющий x и y . [ x , y ] {\displaystyle [x,y]}

АПсевдовогнутая функция — это функция, отрицательное значение которой является псевдовыпуклым.Псевдолинейная функция — это функция, которая является как псевдовыпуклой, так и псевдовогнутой.[4]Например,дробно-линейные программыимеют псевдолинейныецелевые функциииограничения линейно-неравенства. Эти свойства позволяют решать дробно-линейные задачи с помощью вариантасимплексного алгоритма(Джорджа Б. Данцига).[5][6][7]

Для заданной векторной функции существует более общее понятие -псевдовыпуклости [8] [9] и -псевдолинейности; при этом классическая псевдовыпуклость и псевдолинейность относятся к случаю, когда . η {\displaystyle \eta } η {\displaystyle \eta } η {\displaystyle \eta } η ( x , y ) = y − x {\displaystyle \eta (x,y)=y-x}

Смотрите также

Примечания

  1. ^ Мангасарян 1965
  2. ^ Мангасарян 1965
  3. ^ Флудас и Пардалос 2001
  4. ^ Рапчак 1991
  5. ↑ Глава пятая: Craven, BD (1988). Дробное программирование . Серия Sigma в прикладной математике. Том 4. Берлин: Heldermann Verlag. С. 145. ISBN 3-88538-404-3. МР  0949209.
  6. ^ Крук, Серж; Волкович, Генри (1999). «Псевдолинейное программирование». Обзор SIAM . 41 (4): 795– 805. Bibcode : 1999SIAMR..41..795K. doi : 10.1137/S0036144598335259. JSTOR  2653207. MR  1723002.
  7. ^ Матис, Фрэнк Х.; Матис, Ленора Джейн (1995). «Алгоритм нелинейного программирования для управления больницей». Обзор SIAM . 37 (2): 230– 234. doi :10.1137/1037046. JSTOR  2132826. MR  1343214. S2CID  120626738.
  8. ^ Ансари, Камрул Хасан; Лалита, CS; Мехта, Моника (2013). Обобщенная выпуклость, негладкие вариационные неравенства и негладкая оптимизация. CRC Press. стр. 107. ISBN 9781439868218. Получено 15 июля 2019 г. .
  9. ^ Мишра, Шаши К.; Джорджи, Джорджио (2008). Invexity and Optimization. Springer Science & Business Media. стр. 39. ISBN 9783540785613. Получено 15 июля 2019 г. .

Ссылки

  • Floudas, Christodoulos A .; Pardalos, Panos M. (2001), "Обобщенные монотонные многозначные отображения", Encyclopedia of Optimization , Springer, стр. 227, ISBN 978-0-7923-6932-5.
  • Мангасарян, О.Л. (январь 1965 г.). «Псевдовыпуклые функции». Журнал Общества промышленной и прикладной математики, серия А. 3 (2): 281–290 . doi : 10.1137/0303020. ISSN  0363-0129..
  • Рапчак, Т. (1991-02-15). «О псевдолинейных функциях». Европейский журнал операционных исследований . 50 (3): 353– 360. doi :10.1016/0377-2217(91)90267-Y. ISSN  0377-2217.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Pseudoconvex_function&oldid=1143488171"