Библиотека фрагментов белка

Библиотеки фрагментов белковой основы успешно использовались в различных приложениях структурной биологии , включая моделирование гомологии , ^[1] прогнозирование структуры de novo , ^[2]^[3]^[4] и определение структуры . ^[5] Уменьшая сложность пространства поиска, эти библиотеки фрагментов обеспечивают более быстрый поиск конформационного пространства , что приводит к более эффективным и точным моделям.

Мотивация

Белки могут принимать экспоненциальное число состояний при дискретном моделировании. Обычно конформации белка представляются как наборы двугранных углов , длин связей и углов связей между всеми связанными атомами. Наиболее распространенным упрощением является предположение идеальных длин связей и углов связей. Однако это все еще оставляет углы фи-пси основной цепи и до четырех двугранных углов для каждой боковой цепи , что приводит к наихудшей сложности k ^{6* n} возможных состояний белка, где n — количество остатков, а k — количество дискретных состояний, смоделированных для каждого двугранного угла. Чтобы уменьшить конформационное пространство, можно использовать библиотеки фрагментов белка, а не явно моделировать каждый угол фи-пси.

Фрагменты представляют собой короткие сегменты пептидного остова, обычно длиной от 5 до 15 остатков , и не включают боковые цепи. Они могут указывать местоположение только атомов C-альфа, если это редуцированное представление атома, или всех тяжелых атомов остова (N, C-альфа, C карбонил, O). Обратите внимание, что боковые цепи обычно не моделируются с использованием подхода библиотеки фрагментов. Для моделирования дискретных состояний боковой цепи можно использовать подход библиотеки ротамеров . ^[6]

Этот подход работает в предположении, что локальные взаимодействия играют большую роль в стабилизации общей конформации белка. В любой короткой последовательности молекулярные силы ограничивают структуру, что приводит лишь к небольшому числу возможных конформаций, которые можно смоделировать фрагментами. Действительно, согласно парадоксу Левинталя , белок не может перебрать все возможные конформации в течение биологически разумного периода времени. Локально стабилизированные структуры сократили бы пространство поиска и позволили бы белкам сворачиваться порядка миллисекунд.

Строительство

Кластеризация фрагментов. — Кластеризация схожих фрагментов. Центроид показан синим цветом.

Библиотеки этих фрагментов строятся на основе анализа Protein Data Bank (PDB). Сначала выбирается репрезентативное подмножество PDB, которое должно охватывать разнообразный массив структур, желательно с хорошим разрешением. Затем для каждой структуры каждый набор из n последовательных остатков берется в качестве фрагмента образца. Затем образцы кластеризуются в k групп на основе того, насколько они похожи друг на друга в пространственной конфигурации, с использованием таких алгоритмов, как кластеризация k -средних . Параметры n и k выбираются в соответствии с применением (см. обсуждение сложности ниже). Затем центроиды кластеров берутся для представления фрагмента. Дальнейшая оптимизация может быть выполнена для того, чтобы гарантировать, что центроид обладает идеальной геометрией связи, как это было получено путем усреднения других геометрий. ^[7]

Поскольку фрагменты получены из структур, существующих в природе, сегмент остова, который они представляют, будет иметь реалистичные геометрии связей. Это помогает избежать необходимости исследовать все пространство углов конформации, большая часть которых привела бы к нереалистичным геометриям.

Кластеризация выше может быть выполнена без учета идентичности остатков или может быть специфичной для остатков. ^[2] То есть, для любой заданной входной последовательности аминокислот кластеризация может быть получена с использованием только образцов, найденных в PDB с той же последовательностью во фрагменте k -мера. Это требует больше вычислительной работы, чем получение библиотеки фрагментов, независимой от последовательности, но потенциально может дать более точные модели. И наоборот, требуется больший набор образцов, и можно не достичь полного покрытия.

Пример использования: моделирование цикла

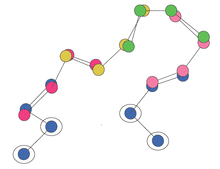
Петлевая конструкция. — Петля длиной 10, построенная с использованием 6 фрагментов, каждый длиной 4. В этой 2D-модели использовались только перекрытия в 2. Точки привязки обведены кружками.

В моделировании гомологии распространенным применением библиотек фрагментов является моделирование петель структуры. Обычно альфа-спирали и бета-слои нанизываются на шаблонную структуру, но петли между ними не указаны и должны быть предсказаны. Поиск петли с оптимальной конфигурацией является NP-трудной задачей . Чтобы уменьшить конформационное пространство, которое необходимо исследовать, можно смоделировать петлю как ряд перекрывающихся фрагментов. Затем пространство можно выбрать или, если теперь оно достаточно мало, исчерпывающе перечислить.

Один из подходов к исчерпывающему перечислению выглядит следующим образом. ^[1] Построение цикла начинается с выравнивания всех возможных фрагментов для перекрытия с тремя остатками на N-конце цикла (якорная точка). Затем все возможные варианты выбора для второго фрагмента выравниваются со (всеми возможными вариантами выбора) первого фрагмента, гарантируя, что последние три остатка первого фрагмента перекрываются с первыми тремя остатками второго фрагмента. Это гарантирует, что цепочка фрагментов образует реалистичные углы как внутри фрагмента, так и между фрагментами. Затем это повторяется до тех пор, пока не будет построен цикл с правильной длиной остатков.

Петля должна начинаться на якоре на стороне N и заканчиваться на якоре на стороне C. Поэтому каждая петля должна быть проверена, чтобы увидеть, перекрываются ли ее последние несколько остатков с якорем на конце C. Очень немногие из этих экспоненциальных чисел петель-кандидатов закроют петлю. После отфильтровывания петель, которые не замыкаются, необходимо определить, какая петля имеет оптимальную конфигурацию, определяемую по наименьшей энергии с использованием некоторого силового поля молекулярной механики.

Сложность

Сложность пространства состояний все еще экспоненциальна по числу остатков, даже после использования библиотек фрагментов. Однако степень экспоненты уменьшается. Для библиотеки фрагментов F -мера с L фрагментами в библиотеке и для моделирования цепочки из N остатков, перекрывающих каждый фрагмент на 3, будет L ^{[ N /( F -3)]+1} возможных цепей. ^[7] Это намного меньше, чем K ^N возможностей, если явно моделировать углы фи-пси как K возможных комбинаций, поскольку сложность растет при степени, меньшей N .

Сложность увеличивается с L , размером библиотеки фрагментов. Однако библиотеки с большим количеством фрагментов будут захватывать большее разнообразие структур фрагментов, поэтому существует компромисс между точностью модели и скоростью исследования пространства поиска. Этот выбор определяет, какой K используется при выполнении кластеризации.

Кроме того, для любого фиксированного L разнообразие структур, которые можно смоделировать, уменьшается с увеличением длины фрагментов. Более короткие фрагменты более способны охватить разнообразный массив структур, обнаруженных в PDB, чем более длинные. Недавно было показано, что библиотеки длиной до 15 способны моделировать 91% фрагментов в PDB с точностью до 2,0 ангстрем. ^[8]

Смотрите также

Ссылки

^ ab Kolodny, R., Guibas, L., Levitt, M., and Koehl, P. (2005, март). Обратная кинематика в биологии: проблема замыкания белковой петли. Международный журнал исследований робототехники 24(2-3), 151-163.
^ ab Simons, K., Kooperberg, C., Huang, E., and Baker, D. (1997). Сборка третичных структур белков из фрагментов с похожими локальными последовательностями с использованием имитации отжига и байесовских функций оценки. J Mol Biol 268, 209-225.
^ Буйницки, Дж. (2006) Прогнозирование структуры белка путем рекомбинации фрагментов. ChemBioChem. 7, 19-27.
^ Ли, С. и др. (2008) Фрагмент-HMM: новый подход к предсказанию структуры белка. Protein Science. 17, 1925-1934.
^ ДиМайо, Ф., Шавлик, Дж., Филлипс, Г. Вероятностный подход к трассировке белковой цепи на картах электронной плотности (2006). Биоинформатика 22(14), 81-89.
^ Кэнутеску, А., Шеленков, А. и Данбрак, Р. (2003). Алгоритм теории графов для предсказания боковой цепи белка. Protein Sci. 12, 2001–2014.
^ ab Колодни, Р., Кёль, П., Гибас, Л. и Левитт, М. (2005). Малые библиотеки фрагментов белков точно моделируют структуры нативных белков. J Mol Biol 323, 297-307.
^ Ду, П., Андрек, М. и Леви, Р. Видели ли мы все структуры, соответствующие коротким фрагментам белков в банке данных белков? Обновление. Белковая инженерия. 2003, 16(6) 407-414.

[KolodnyLoop-1] Kolodny, R., Guibas, L., Levitt, M., and Koehl, P. (2005, март). Обратная кинематика в биологии: проблема замыкания белковой петли. Международный журнал исследований робототехники 24(2-3), 151-163.

[Baker1997-2] Simons, K., Kooperberg, C., Huang, E., and Baker, D. (1997). Сборка третичных структур белков из фрагментов с похожими локальными последовательностями с использованием имитации отжига и байесовских функций оценки. J Mol Biol 268, 209-225.

[Bujnicki-3] Буйницки, Дж. (2006) Прогнозирование структуры белка путем рекомбинации фрагментов. ChemBioChem. 7, 19-27.

[LiFragmentHMM-4] Ли, С. и др. (2008) Фрагмент-HMM: новый подход к предсказанию структуры белка. Protein Science. 17, 1925-1934.

[DiMaio-5] ДиМайо, Ф., Шавлик, Дж., Филлипс, Г. Вероятностный подход к трассировке белковой цепи на картах электронной плотности (2006). Биоинформатика 22(14), 81-89.

[dunbrackLib-6] Кэнутеску, А., Шеленков, А. и Данбрак, Р. (2003). Алгоритм теории графов для предсказания боковой цепи белка. Protein Sci. 12, 2001–2014.

[KolodnyLibrary-7] Колодни, Р., Кёль, П., Гибас, Л. и Левитт, М. (2005). Малые библиотеки фрагментов белков точно моделируют структуры нативных белков. J Mol Biol 323, 297-307.

[DuAllFragments-8] Ду, П., Андрек, М. и Леви, Р. Видели ли мы все структуры, соответствующие коротким фрагментам белков в банке данных белков? Обновление. Белковая инженерия. 2003, 16(6) 407-414.